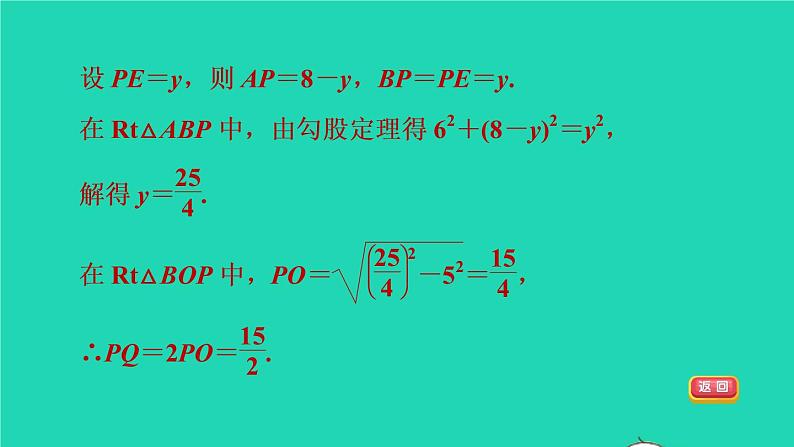
2021学年第19章 四边形综合与测试习题ppt课件

这是一份2021学年第19章 四边形综合与测试习题ppt课件，共23页。PPT课件主要包含了习题链接等内容，欢迎下载使用。

如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD，BE，BC于点P，O，Q，连接BP，EQ．(1)求证：四边形BPEQ是菱形；
∴△BOQ≌△EOP(ASA)．∴QB＝PE.∵BC∥AD，∴四边形BPEQ是平行四边形．又∵QB＝QE，∴四边形BPEQ是菱形．
(2)若AB＝6，F为AB的中点，OF＋OB＝9，求PQ的长．
【中考·海南】如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点(与点A，D不重合)，射线PE与BC的延长线交于点Q．(1)求证：△PDE≌△QCE．
证明：∵四边形ABCD是正方形，∴∠D＝∠BCD＝90°.∴∠ECQ＝90°＝∠D.∵E是CD的中点，∴DE＝CE.又∵∠DEP＝∠CEQ，∴△PDE≌△QCE(ASA)．
(2)过点E作EF∥BC交PB于点F，连接AF，当PB＝PQ时．①求证：四边形AFEP是平行四边形；
②请判断四边形AFEP是否为菱形，并说明理由．
解：四边形AFEP不是菱形．理由如下：设PD＝x，则AP＝1－x.由(1)可知△PDE≌△QCE，∴CQ＝PD＝x.∴BQ＝BC＋CQ＝1＋x.∵点E，F分别是PQ，PB的中点，∴EF是△PBQ的中位线．
如图，在矩形ABCD中，∠ABC的平分线交对角线AC于点M，ME⊥AB，MF⊥BC，垂足分别是E，F，判定四边形MEBF的形状，并证明你的结论．
解：四边形MEBF是正方形．证明如下：∵四边形ABCD是矩形，∴∠ABC＝90°.∵ME⊥AB，MF⊥BC，∴∠MEB＝∠MFB＝90°.∴四边形MEBF是矩形．又∵BM是∠ABC的平分线，∴ME＝MF.∴矩形MEBF是正方形．
如图，在△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△ABC的外角∠ACD的平分线于点F．(1)探究OE与OF的数量关系并加以证明．
解：OE＝OF.证明：∵MN∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF.又∵CE平分∠BCO，CF平分∠DCO，∴∠OCE＝∠BCE，∠OCF＝∠DCF.∴∠OCE＝∠OEC，∠OCF＝∠OFC.∴EO＝CO，FO＝CO. ∴OE＝OF.
(2)连接BE，当点O在边AC上运动时，四边形BCFE能否为菱形？若能，请证明；若不能，请说明理由．
若四边形BCFE是菱形，则BF⊥EC，在△GFC中，不可能存在两个角为90°，∴四边形BCFE不可能为菱形．
(3)连接AE，AF，当点O在边AC上运动到什么位置时，四边形AECF是矩形？请说明理由．
解：当点O运动到AC的中点时，四边形AECF是矩形．理由：当点O运动到AC的中点时，AO＝CO.又∵EO＝FO，∴四边形AECF是平行四边形．∵FO＝CO，∴AO＝CO＝EO＝FO.∴AO＋CO＝EO＋FO，即AC＝EF.∴四边形AECF是矩形．
(4)在(3)的条件下，△ABC满足什么条件时，四边形AECF是正方形？请说明理由．