2020-2021学年19.3 矩形 菱形 正方形习题课件ppt

这是一份2020-2021学年19.3 矩形 菱形 正方形习题课件ppt，共20页。PPT课件主要包含了答案呈现等内容，欢迎下载使用。
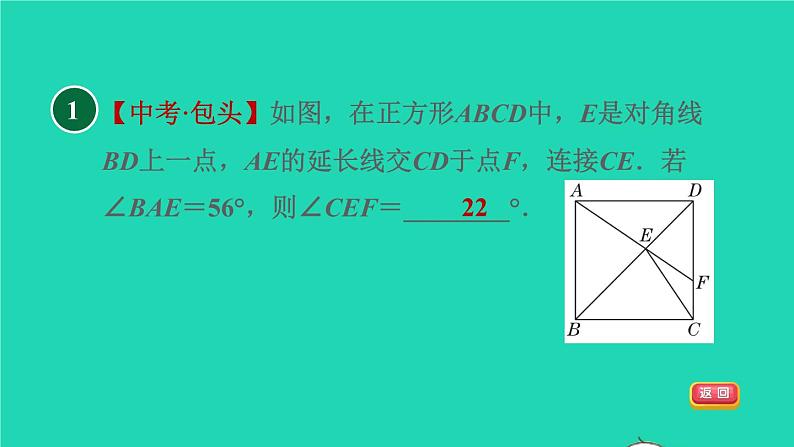
【中考·包头】如图，在正方形ABCD中，E是对角线BD上一点，AE的延长线交CD于点F，连接CE．若∠BAE＝56°，则∠CEF＝________°．
【中考·枣庄】如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是________．
【中考·呼伦贝尔】已知：如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F分别是边BC，CD上的点，且∠EOF＝90°．求证：CE＝DF．
证明：∵四边形ABCD为正方形，∴OD＝OC，∠ODF＝∠OCE＝45°，∠COD＝90°.∴∠DOF＋∠COF＝90°.∵∠EOF＝90°，即∠COE＋∠COF＝90°，∴∠COE＝∠DOF. ∴△COE≌△DOF(ASA)．∴CE＝DF.
【中考·宜昌】如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB，EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J，则图中阴影部分的面积等于(　　)
如图，点E在正方形ABCD的对角线AC上，且EC＝2AE，Rt△FEG的两条直角边EF，EG分别交BC，DC于点M，N，若正方形ABCD的边长为a，则阴影部分即四边形EMCN的面积为(　　)
【点拨】如图，过点E作EO⊥CD于点O，EH⊥BC于点H，易知四边形EHCO为正方形，∴EH＝EO，∠HEO＝90°.∵∠GEF＝∠HEO＝90°，∴∠OEN＝∠MEH.又∵∠EHM＝∠EON＝90°，∴△EHM≌△EON(ASA)．
【中考·孝感】如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝3，CG＝2，则CE的长为(　　)
【点拨】如图，连接EG，由题易知F在CB的延长线上．由旋转可得△ADE≌△ABF，∴AE＝AF，DE＝BF.又∵AG⊥EF，∴H为EF的中点，∴AG垂直平分EF. ∴EG＝FG.
【中考·湘西州】如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE．(1)求证：△BAE≌△CDE；
(2)求∠AEB的度数．
【中考·武威】如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN＝45°．把△ADN绕点A顺时针旋转90°得到△ABE．(1)求证：△AEM≌△ANM；
证明：∵把△ADN绕点A顺时针旋转90°得到△ABE，∴△ADN≌△ABE.∴∠DAN＝∠BAE，DN＝BE，AN＝AE.由题易知E在CB的延长线上．∵∠DAB＝90°，∠MAN＝45°，∴∠MAE＝∠BAE＋∠BAM＝∠DAN＋∠BAM＝45°.∴∠MAE＝∠MAN.又∵MA＝MA，AE＝AN，∴△AEM≌△ANM(SAS)．
(2)若BM＝3，DN＝2，求正方形ABCD的边长．
解：设CD＝BC＝x，则CM＝x－3，CN＝x－2.∵△AEM≌△ANM，∴EM＝MN.∵BE＝DN，∴MN＝EM＝BM＋BE＝BM＋DN＝5.∵∠C＝90°，∴MN2＝CM2＋CN2，即52＝(x－3)2＋(x－2)2. 化简，得x2－5x－6＝0.因式分解，得(x－6)(x＋1)＝0.