2021-2022学年河南省新乡市某校初二（下）期中考试数学试卷人教版

这是一份2021-2022学年河南省新乡市某校初二（下）期中考试数学试卷人教版，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

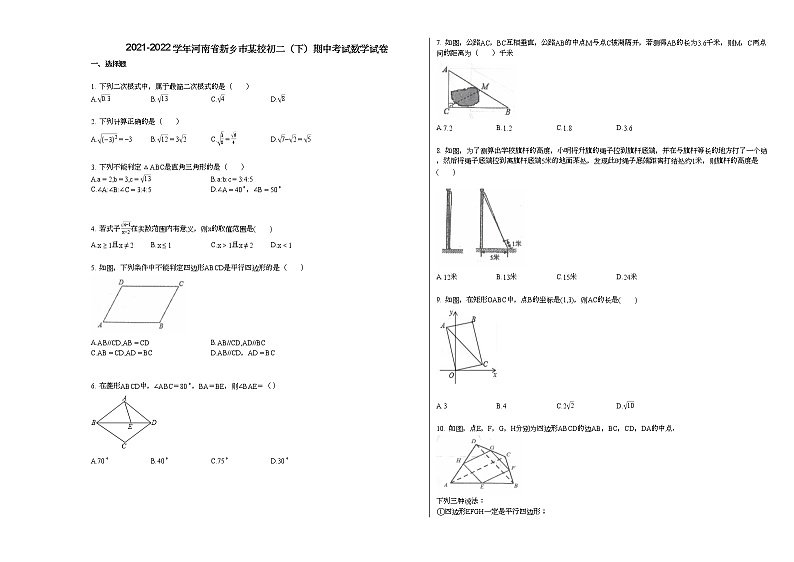
1. 下列二次根式中，属于最简二次根式的是（ ）
A.0.3B.13C.4D.8

2. 下列计算正确的是（ ）
A.−32=−3B.12=32C.38=64D.7−2=5

3. 下列不能判定△ABC是直角三角形的是（ ）
A.a=2,b=3,c=13B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5D.∠A=40∘，∠B=50∘

4. 若式子x−1x−2在实数范围内有意义，则x的取值范围是( )
A.x≥1且x≠2B.x≤1C.x>1且x≠2D.xAD，将矩形纸片沿过点A的直线折叠，使点B落在边AD上，点B的对应点为F，折痕为AE，点E在BC上．求证：四边形ABEF是正方形．（请完成以下填空）
证明：∵ 四边形ABCD是矩形，∴ ∠BAD=∠B=90∘，
∵ 折叠，∴ ∠AFE=∠B=90∘，
∴ 四边形ABEF是矩形（________）
∵ 折叠，∴ AB=________，
∴ 四边形ABEF是正方形（________）
【问题拓展】如图2，已知平行四边形纸片ABCDAD>AB，将平行四边形纸片沿过点A的直线折叠，使点B落在边AD上，点B的对应点为F折痕为AE，点E在边BC上．
（1）求证：四边形ABEF是菱形．
（2）连结BF，若AE=5,BF=10，则菱形ABEF的面积为________.


下面是张华设计的尺规作图．
已知：矩形ABCD．
作法：
①分别以A，B为圆心，以大于12AB长为半径，在AB两侧作弧，分别交于点E， F；
②作直线EF；
③以点A为圆心，AB为半径作弧，交直线EF于点G，连接AG，BG；
根据张华设计的尺规作图，解决下列问题：
（1）求∠BAG的度数；
（2）过点D作DH//AG，交直线EF于点H．
①求证：四边形AGHD为平行四边形．
②用等式表示平行四边形AGHD的面积S1和矩形ABCD的面积S2的数量关系为________.
参考答案与试题解析
2021-2022学年河南省新乡市某校初二（下）期中考试数学试卷
一、选择题
1.
【答案】
B
【考点】
最简二次根式
【解析】
此题暂无解析
【解答】
B
2.
【答案】
C
【考点】
二次根式的性质与化简
【解析】
此题暂无解析
【解答】
C
3.
【答案】
C
【考点】
三角形内角和定理
勾股定理的逆定理
【解析】
此题暂无解析
【解答】
C
4.
【答案】
A
【考点】
分式有意义、无意义的条件
二次根式有意义的条件
【解析】
分式有意义，分母不等于零；二次根式的被开方数是非负数．
【解答】
解：式子x−1x−2在实数范围内有意义，得
x−1≥0且x−2≠0，
解得x≥1且x≠2．
故选A.
5.
【答案】
D
【考点】
平行四边形的判定
【解析】
此题暂无解析
【解答】
D
6.
【答案】
A
【考点】
菱形的性质
等腰三角形的性质
【解析】
利用菱形的性质和等腰三角形的性质即可求解．
【解答】
A
7.
【答案】
C
【考点】
直角三角形斜边上的中线
【解析】
此题暂无解析
【解答】
C
8.
【答案】
A
【考点】
勾股定理的应用
【解析】
此题暂无解析
【解答】
A
9.
【答案】
D
【考点】
矩形的性质
勾股定理
点的坐标
【解析】
此题暂无解析
【解答】
D
10.
【答案】
D
【考点】
矩形的判定
平行四边形的判定
中点四边形
三角形中位线定理
菱形的判定
【解析】
此题暂无解析
【解答】
D
二、填空题
【答案】
5
【考点】
在数轴上表示实数
【解析】
此题暂无解析
【解答】
5
【答案】
15
【考点】
勾股定理的综合与创新
正方形的性质
【解析】
根据勾股定理的几何意义解答．
【解答】
15
【答案】
南偏东50∘
【考点】
勾股定理
方向角
【解析】
此题暂无解析
【解答】
南偏东50∘
【答案】
20
【考点】
菱形的判定与性质
矩形的性质
【解析】
此题暂无解析
【解答】
20
【答案】
(2,3)
【考点】
坐标与图形性质
勾股定理
正方形的性质
【解析】
由已知条件得到AD′=AD=2，AO=12AB=1，根据勾股定理得到OD′=AD′2−OA2=3，于是得到结论.
【解答】
解：∵AD′=AD=2，
AO=12AB=1，
∴OD′=AD′2−OA2=3，
∵C′D′=2，C′D′//AB，
∴C′(2,3)．
故答案为：(2,3)．
三、解答题
【答案】
解：（1）原式=43−23+33=53
（2）原式=9−65+5+25=14−45
【考点】
二次根式的混合运算
【解析】
此题暂无解析
【解答】
解：（1）原式=43−23+33=53
（2）原式=9−65+5+25=14−45
【答案】
解：（1）∵ 四边形ABCD是平行四边形，∴ BO=DO
∵ 点E是CD的中点，∴ BC=2OE=10
（2）∵ AC⊥AB，∴ ∠BAC=90∘，∴ AC=BC2−AB2=102−62=8
∴ 平行四边形的面积=6×8=48．
【考点】
平行四边形的性质
勾股定理
【解析】
此题暂无解析
【解答】
解：（1）∵ 四边形ABCD是平行四边形，∴ BO=DO
∵ 点E是CD的中点，∴ BC=2OE=10
（2）∵ AC⊥AB，∴ ∠BAC=90∘，∴ AC=BC2−AB2=102−62=8
∴ 平行四边形的面积=6×8=48．
【答案】
解：能救下
由题意得： BD=CE=9,AB=15，
在Rt△ABD中， AD=AB2−BD2=152−92=12
∴ AE=AD+DE=12+2=14 （米） >13米，所以能救下．
【考点】
勾股定理的应用
【解析】
此题暂无解析
【解答】
解：能救下
由题意得： BD=CE=9,AB=15，
在Rt△ABD中， AD=AB2−BD2=152−92=12
∴ AE=AD+DE=12+2=14 （米） >13米，所以能救下．
【答案】
(1)证明：∵ 四边形ABCD是平行四边形，
∴ AF//BE.
∵ AF=BE，
∴ 四边形ABEF是平行四边形.
∵ BA=BE，
∴ 平行四边形ABEF是菱形.
(2)解：如图所示，连接AE，BF交于点P，
点P即为所求（菱形的对角线互相垂直）.
【考点】
平行四边形的性质
作图—复杂作图
菱形的判定与性质
【解析】
（1）根据平行四边形的性质和判定，菱形的判定即可证明；
（2）连结AE，BF，根据菱形的性质可得AE和BF的交点即为点P．
【解答】
(1)证明：∵ 四边形ABCD是平行四边形，
∴ AF//BE.
∵ AF=BE，
∴ 四边形ABEF是平行四边形.
∵ BA=BE，
∴ 平行四边形ABEF是菱形.
(2)解：如图所示，连接AE，BF交于点P，
点P即为所求（菱形的对角线互相垂直）.
【答案】
解：（1） △ABC的面积=4×4−12×2×4−12×2×1−12×4×3=5
（2）由勾股定理得：AC2=42+22=20，
BC2=22+12=5，AB2=32+42=25，
∴ AC2+BC2=AB2，
∴ ∠ACB=90∘，即△ABC是直角三角形.
（3）由（2）得，AC=20=25，
BC=5，AB=5，∠ACB=90∘，，
∴ AB边上的高为：AC⋅BCAB=25×55=2．
【考点】
三角形的面积
勾股定理的逆定理
勾股定理
【解析】


【解答】
解：（1） △ABC的面积=4×4−12×2×4−12×2×1−12×4×3=5
（2）由勾股定理得：AC2=42+22=20，
BC2=22+12=5，AB2=32+42=25，
∴ AC2+BC2=AB2，
∴ ∠ACB=90∘，即△ABC是直角三角形.
（3）由（2）得，AC=20=25，
BC=5，AB=5，∠ACB=90∘，，
∴ AB边上的高为：AC⋅BCAB=25×55=2．
【答案】
（1）证明：∵ 四边形ABCD是平行四边形，
∴ DC//AB，
∴ DF//BE
又∵ DF=BE，∴ 四边形BFDE是平行四边形
∵ DE⊥AB，∴ 平行四边形BFDE是矩形．
（2）解：∵ AB//CD，
∴ ∠BAF=∠AFD，
∵ A，F平分∠BAD，
∴ ∠DAF=∠AFD，
∴ AD=DF
在Rt△ADE中，∵ AE=6 ，DE=8，
∴ AD=62+82=10，
∴ 矩形的面积为8×10=80 .
【考点】
平行四边形的性质
矩形的判定与性质
勾股定理
【解析】
此题暂无解析
【解答】
（1）证明：∵ 四边形ABCD是平行四边形，
∴ DC//AB，
∴ DF//BE
又∵ DF=BE，∴ 四边形BFDE是平行四边形
∵ DE⊥AB，∴ 平行四边形BFDE是矩形．
（2）解：∵ AB//CD，
∴ ∠BAF=∠AFD，
∵ A，F平分∠BAD，
∴ ∠DAF=∠AFD，
∴ AD=DF
在Rt△ADE中，∵ AE=6 ，DE=8，
∴ AD=62+82=10，
∴ 矩形的面积为8×10=80 .
【答案】
【问题解决】有三个角是直角的四边形是矩形
AF
一组邻边相等的矩形是正方形．
【问题拓展】证明：（1）由折叠得AB=AF,∠BAE=∠EAE，
∵ 四边形ABCD是平行四边形，
∴ AD//BC，即AF//BE．
∴ ∠BEA=∠FAE，
∴ ∠BEA=∠BAE，
∴ AB=BE，
∴ AF=BE，
∵ AF//BE，
∴ 四边形ABEF是平行四边形，
∵ AB=AF，
∴ ▱ABEF是菱形；
（2）25
【考点】
菱形的判定与性质
翻折变换（折叠问题）
矩形的性质
【解析】
此题暂无解析
【解答】
【问题解决】有三个角是直角的四边形是矩形
AF
一组邻边相等的矩形是正方形．
【问题拓展】证明：（1）由折叠得AB=AF,∠BAE=∠EAE，
∵ 四边形ABCD是平行四边形，
∴ AD//BC，即AF//BE．
∴ ∠BEA=∠FAE，
∴ ∠BEA=∠BAE，
∴ AB=BE，
∴ AF=BE，
∵ AF//BE，
∴ 四边形ABEF是平行四边形，
∵ AB=AF，
∴ ▱ABEF是菱形；
（2）25
【答案】
解：（1）由作图知，EF是线段AB的垂直平分线，
∴ AG=BG，
∵ AB=AG，
∴ AB=AG=BG，
∴ △ABG是等边三角形，
∴ ∠BAG=60∘ ．
（2）①∵ 四边形ABCD是矩形，
∴ ∠BAD=90∘，
∵ EF⊥AB，
∴ GH//AD，
又∵ DH//AG，
∴ 四边形AGHD是平行四边形．
②S2=2S1 ．
【考点】
矩形的性质
线段垂直平分线的性质
平行四边形的判定
【解析】
此题暂无解析
【解答】
解：（1）由作图知，EF是线段AB的垂直平分线，
∴ AG=BG，
∵ AB=AG，
∴ AB=AG=BG，
∴ △ABG是等边三角形，
∴ ∠BAG=60∘ ．
（2）①∵ 四边形ABCD是矩形，
∴ ∠BAD=90∘，
∵ EF⊥AB，
∴ GH//AD，
又∵ DH//AG，
∴ 四边形AGHD是平行四边形．
②S2=2S1 ．