2021-2022学年湖南省湘西古丈县重点中学中考联考数学试题含解析

2021-2022中考数学模拟试卷

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）

1．在数轴上表示不等式2（1﹣x）＜4的解集，正确的是（　　）

A． B．

C． D．

2．若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根，则m的取值范围是（　　）

A．m＜﹣1 B．m＜1 C．m＞﹣1 D．m＞1

3．估算的值在(    )

A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间

4．对于两组数据A，B，如果sA2＞sB2，且，则（　　）

A．这两组数据的波动相同 B．数据B的波动小一些

C．它们的平均水平不相同 D．数据A的波动小一些

5．一个几何体的俯视图如图所示，其中的数字表示该位置上小正方体的个数，那么这个几何体的主视图是（　　）

A． B． C． D．

6．古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（　　）

A．13＝3+10 B．25＝9+16 C．36＝15+21 D．49＝18+31

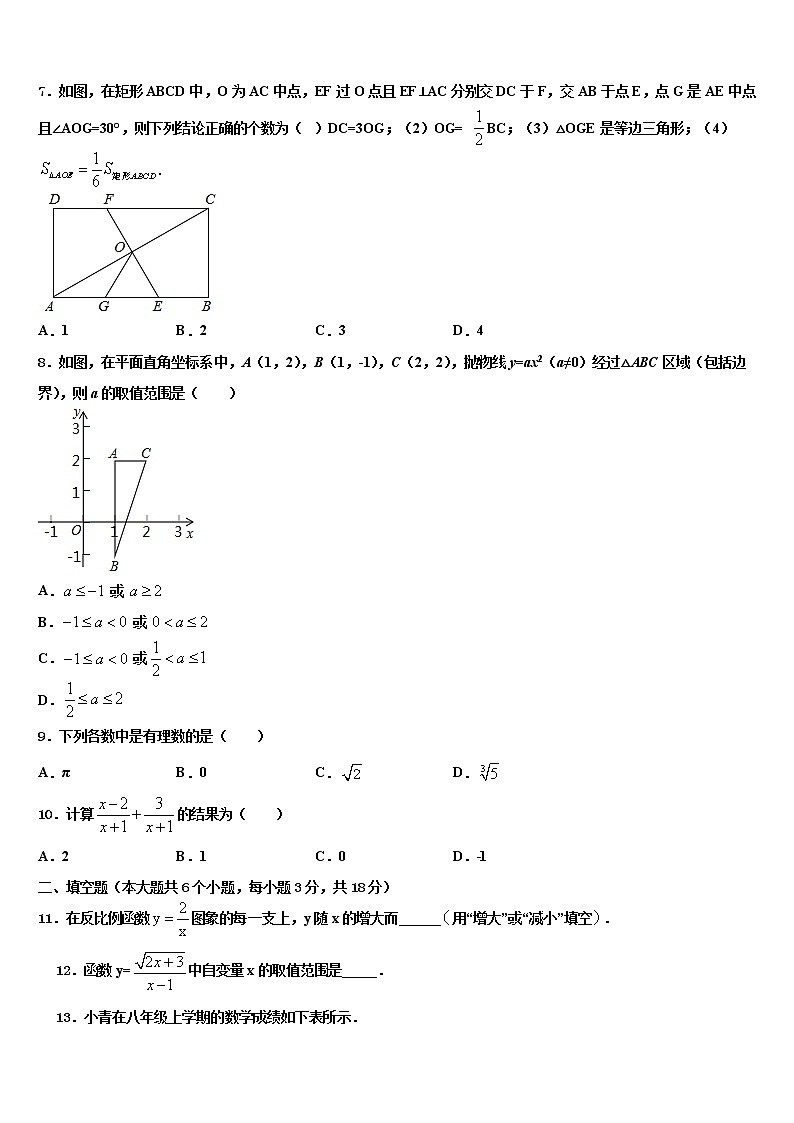
7．如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB于点E，点G是AE中点且∠AOG=30°，则下列结论正确的个数为（  ）DC=3OG；（2）OG= BC；（3）△OGE是等边三角形；（4）.

A．1 B．2 C．3 D．4

8．如图，在平面直角坐标系中，A（1，2），B（1，-1），C（2，2），抛物线y=ax2（a≠0）经过△ABC区域（包括边界），则a的取值范围是（　　）

A． 或 

B． 或 

C． 或

D．

9．下列各数中是有理数的是（　　）

A．π B．0 C． D．

10．计算的结果为（　　）

A．2 B．1 C．0 D．﹣1

二、填空题（本大题共6个小题，每小题3分，共18分）

11．在反比例函数图象的每一支上，y随x的增大而______用“增大”或“减小”填空．

12．函数y=中自变量x的取值范围是_____．

13．小青在八年级上学期的数学成绩如下表所示．

如果学期总评成绩根据如图所示的权重计算，小青该学期的总评成绩是_____分．

14．株洲市城区参加2018年初中毕业会考的人数约为10600人，则数10600用科学记数法表示为_____．

15．在一个不透明的布袋中，红色、黑色的玻璃球共有20个，这些球除颜色外其它完全相同．将袋中的球搅匀，从中随机摸出一个球，记下颜色后再放回袋中，不断地重复这个过程，摸了200次后，发现有60次摸到黑球，请你估计这个袋中红球约有_____个．

16．一元二次方程x2+mx+3=0的一个根为- 1，则另一个根为            ．

三、解答题（共8题，共72分）

17．（8分）如图，AC⊥BD，DE交AC于E，AB＝DE，∠A＝∠D．求证：AC＝AE+BC．

18．（8分）如图，直角坐标系中，直线与反比例函数的图象交于A，B两点，已知A点的纵坐标是2.

（1）求反比例函数的解析式.

（2）将直线沿x轴向右平移6个单位后，与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动，当线段PA与线段PC之差达到最大时，求点P的坐标.

19．（8分）经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转．如果这三种可能性大小相同，现有两辆汽车经过这个十字路口．

(1)试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果；并计算两辆汽车都不直行的概率．

(2)求至少有一辆汽车向左转的概率．

20．（8分）（1）计算：|﹣2|﹣（π﹣2015）0+（）﹣2﹣2sin60°+；

(2)先化简，再求值：÷（2+），其中a= ．

21．（8分）为落实“垃圾分类”，环卫部门要求垃圾要按A,B,C三类分别装袋,投放，其中A类指废电池,过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类．直接写出甲投放的垃圾恰好是A类的概率；求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率．

22．（10分）校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=30，∠CBD=60．求AB的长(精确到0.1米，参考数据：)；已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由．

23．（12分）解方程：．

24．如图，在菱形ABCD中，作于E，BF⊥CD于F，求证：．

参考答案

一、选择题（共10小题，每小题3分，共30分）

1、A

【解析】

根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得不等式解集，然后得出在数轴上表示不等式的解集．    2(1– x)＜4

去括号得：2﹣2ｘ＜4

移项得：2x＞﹣2，

系数化为1得：x＞﹣1，

故选A．   

“点睛”本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．

2、B

【解析】
根据方程有两个不相等的实数根结合根的判别式即可得出△=4-4m＞0，解之即可得出结论．

【详解】

∵关于x的一元二次方程x2-2x+m=0有两个不相等的实数根，

∴△=（-2）2-4m=4-4m＞0，

解得：m＜1．

故选B．

【点睛】

本题考查了根的判别式，熟练掌握“当△＞0时，方程有两个不相等的两个实数根”是解题的关键．

3、C

【解析】
由可知56，即可解出.

【详解】

∵

∴56，

故选C.

【点睛】

此题主要考查了无理数的估算，掌握无理数的估算是解题的关键.

4、B

【解析】

试题解析：方差越小，波动越小.

数据B的波动小一些.

故选B.

点睛：本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．

5、A

【解析】
一一对应即可.

【详解】

最左边有一个，中间有两个，最右边有三个，所以选A.

【点睛】

理解立体几何的概念是解题的关键.

6、C

【解析】
本题考查探究、归纳的数学思想方法．题中明确指出：任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．由于“正方形数”为两个“三角形数”之和，正方形数可以用代数式表示为：（n+1）2，两个三角形数分别表示为n（n+1）和（n+1）（n+2），所以由正方形数可以推得n的值，然后求得三角形数的值．

【详解】

∵A中13不是“正方形数”；选项B、D中等式右侧并不是两个相邻“三角形数”之和．

故选：C．

【点睛】

此题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．

7、C

【解析】

∵EF⊥AC，点G是AE中点，

∴OG=AG=GE=AE，

∵∠AOG=30°，

∴∠OAG=∠AOG=30°，

∠GOE=90°-∠AOG=90°-30°=60°，

∴△OGE是等边三角形，故（3）正确；

设AE=2a，则OE=OG=a，

由勾股定理得，AO=，

∵O为AC中点，

∴AC=2AO=2，

∴BC=AC=，

在Rt△ABC中，由勾股定理得，AB==3a，

∵四边形ABCD是矩形，

∴CD=AB=3a，

∴DC=3OG，故（1）正确；

∵OG=a，BC=，

∴OG≠BC，故（2）错误；

∵S△AOE=a•=，

SABCD=3a•=32，

∴S△AOE=SABCD，故（4）正确；

综上所述，结论正确是（1）（3）（4）共3个，

故选C．

【点睛】本题考查了矩形的性质，等边三角形的判定、勾股定理的应用等，正确地识图，结合已知找到有用的条件是解答本题的关键.

8、B

【解析】

试题解析：如图所示：

分两种情况进行讨论：

当时，抛物线经过点时，抛物线的开口最小，取得最大值抛物线经过△ABC区域（包括边界），的取值范围是：

当时，抛物线经过点时，抛物线的开口最小，取得最小值抛物线经过△ABC区域（包括边界），的取值范围是：

故选B.

点睛：二次函数 二次项系数决定了抛物线开口的方向和开口的大小，

开口向上，开口向下.

的绝对值越大，开口越小.

9、B

【解析】

【分析】根据有理数是有限小数或无限循环小数，结合无理数的定义进行判断即可得答案．

【详解】A、π是无限不循环小数，属于无理数，故本选项错误；

B、0是有理数，故本选项正确；

C、是无理数，故本选项错误；

D、是无理数，故本选项错误，

故选B．

【点睛】本题考查了实数的分类，熟知有理数是有限小数或无限循环小数是解题的关键．

10、B

【解析】
按照分式运算规则运算即可，注意结果的化简.

【详解】

解：原式=，故选择B.

【点睛】

本题考查了分式的运算规则.

二、填空题（本大题共6个小题，每小题3分，共18分）

11、减小

【解析】
根据反比例函数的性质，依据比例系数k的符号即可确定．

【详解】

∵k=2＞0，

∴y随x的增大而减小．

故答案是：减小．

【点睛】

本题考查了反比例函数的性质，反比例函数y=（k≠0）的图象是双曲线，当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．

12、x≥﹣且x≠1．

【解析】
根据分式有意义的条件、二次根式有意义的条件列式计算．

【详解】

由题意得，2x+3≥0，x-1≠0，

解得，x≥-且x≠1，

故答案为：x≥-且x≠1．

【点睛】

本题考查的是函数自变量的取值范围，①当表达式的分母不含有自变量时，自变量取全体实数．②当表达式的分母中含有自变量时，自变量取值要使分母不为零．③当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．

13、84.2

【解析】

小青该学期的总评成绩为:86×10%+90×30%+81×60%=84.2（分）,故答案为: 84.2.

14、1.06×104

【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【详解】

解：10600＝1.06×104，

故答案为：1.06×104

【点睛】

此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

15、1

【解析】
估计利用频率估计概率可估计摸到黑球的概率为0.3，然后根据概率公式计算这个口袋中黑球的数量，继而得出答案．

【详解】

因为共摸了200次球，发现有60次摸到黑球，

所以估计摸到黑球的概率为0.3，

所以估计这个口袋中黑球的数量为20×0.3=6（个），

则红球大约有20-6=1个，

故答案为：1．

【点睛】

本题考查了利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．用频率估计概率得到的是近似值，随实验次数的增多，值越来越精确．

16、-1.

【解析】
因为一元二次方程的常数项是已知的，可直接利用两根之积的等式求解．

【详解】

∵一元二次方程x2+mx+1=0的一个根为-1，设另一根为x1，

由根与系数关系：-1•x1=1，

解得x1=-1．

故答案为-1.

三、解答题（共8题，共72分）

17、见解析.

【解析】
由“SAS”可证△ABC≌△DEC，可得BC＝CE，即可得结论．

【详解】

证明：∵AB＝DE，∠A＝∠D，∠ACB＝∠DCE＝90°

∴△ABC≌△DEC（SAS）

∴BC＝CE，

∵AC＝AE+CE

∴AC＝AE+BC

【点睛】

本题考查了全等三角形的判定和性质，熟练运用全等三角形的性质是本题的关键．

18、（1）；（2）P（0,6）

【解析】

试题分析：（1）先求得点A的坐标，再利用待定系数法求得反比例函数的解析式即可；（2）连接AC，根据三角形两边之差小于第三边知：当A、C、P不共线时，PA-PC<AC；当A、C、P不共线时，PA-PC=AC；因此，当点P在直线AC与y轴的交点时，PA-PC取得最大值.先求得平移后直线的解析式，再求得平移后直线与反比例函数的图象的交点坐标，最后求直线AC的解析式，即可求得点P的坐标.

试题解析：

令一次函数中，则，

解得：，即点A的坐标为（-4，2）．

∵点A（-4，2）在反比例函数的图象上，

∴k=-4×2=-8，

∴反比例函数的表达式为．

连接AC，根据三角形两边之差小于第三边知：当A、C、P不共线时，PA-PC<AC；当A、C、P不共线时，PA-PC=AC；因此，当点P在直线AC与y轴的交点时，PA-PC取得最大值.  

设平移后直线于x轴交于点F，则F（6，0）

设平移后的直线解析式为，

将F（6，0）代入得：b=3

∴直线CF解析式：  

令3=，解得：，                        

∴C（-2，4）

∵A、C两点坐标分别为A（-4，2）、C（-2，4）

∴直线AC的表达式为，                

此时，P点坐标为P（0，6）.

点睛：本题是一次函数与反比例函数的综合题，主要考查了用待定系数法求函数的解析式、一次函数与反比例函数的交点坐标，熟练运用一次函数及反比例函数的性质是解题的关键.

19、 (1)；(2)．

【解析】
（1）可以采用列表法或树状图求解．可以得到一共有9种情况，从中找到两辆汽车都不直行的结果数，根据概率公式计算可得；

（2）根据树状图得出至少有一辆汽车向左转的结果数，根据概率公式可得答案．

【详解】

(1)画“树形图”列举这两辆汽车行驶方向所有可能的结果如图所示：

∴这两辆汽车行驶方向共有9种可能的结果，其中两辆汽车都不直行的有4种结果，

所以两辆汽车都不直行的概率为；

(2)由(1)中“树形图”知，至少有一辆汽车向左转的结果有5种，且所有结果的可能性相等

∴P（至少有一辆汽车向左转）=．

【点睛】

此题考查了树状图法求概率．解题的关键是根据题意画出树状图，再由概率=所求情况数与总情况数之比求解．

20、（1）5+；（2）

【解析】

试题分析：（1）先分别进行绝对值化简，0指数幂、负指数幂的计算，特殊三角函数值、二次根式的化简，然后再按运算顺序进行计算即可；

（2）括号内先通分进行加法运算，然后再进行分式除法运算，最后代入数值进行计算即可.

试题解析：（1）原式=2﹣1+4﹣2×+2=2﹣1+4﹣+2=5+；

（2）原式==，

当a=时，原式==．

21、（1）（2）．

【解析】
（1）根据总共三种，A只有一种可直接求概率；

（2）列出其树状图，然后求出能出现的所有可能，及符合条件的可能，根据概率公式求解即可．

【详解】

解： (1)甲投放的垃圾恰好是A类的概率是．

(2)列出树状图如图所示：

由图可知，共有18种等可能结果，其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果有12种．

所以， (乙投放的垃圾恰有一袋与甲投放的垃圾是同类)．

即，乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率是．

22、（1）24.2米(2) 超速，理由见解析

【解析】
（1）分别在Rt△ADC与Rt△BDC中，利用正切函数，即可求得AD与BD的长，从而求得AB的长．

（2）由从A到B用时2秒，即可求得这辆校车的速度，比较与40千米/小时的大小，即可确定这辆校车是否超速．

【详解】

解：（1）由題意得，

在Rt△ADC中，，

在Rt△BDC中，，

∴AB=AD－BD=（米）．

（2）∵汽车从A到B用时2秒，∴速度为24.2÷2=12.1（米/秒），

∵12.1米/秒=43.56千米/小时，∴该车速度为43.56千米/小时．

∵43.56千米/小时大于40千米/小时，

∴此校车在AB路段超速．

23、x=，x=﹣2

【解析】
方程两边乘最简公分母，可以把分式方程转化为整式方程求解．

【详解】

，

则2x（x+1）=3（1﹣x），

2x2+5x﹣3=0，

（2x﹣1）（x+3）=0，

解得：x1=，x2=﹣3，

检验：当x=，x=﹣2时，2（x+1）（1﹣x）均不等于0，

故x=，x=﹣2都是原方程的解．

【点睛】

本题考查解分式方程的能力．（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解；（2）解分式方程一定注意要验根；（3）去分母时要注意符号的变化．

24、见解析

【解析】
由菱形的性质可得，，然后根据角角边判定，进而得到.

【详解】

证明：∵菱形ABCD，

∴，，

∵，，

∴，

在与中，

，

∴，

∴．

【点睛】

本题考查菱形的性质和全等三角形的判定与性质，根据菱形的性质得到全等条件是解题的关键.