正方形（难）学案-无答案

这是一份正方形（难）学案-无答案，共4页。
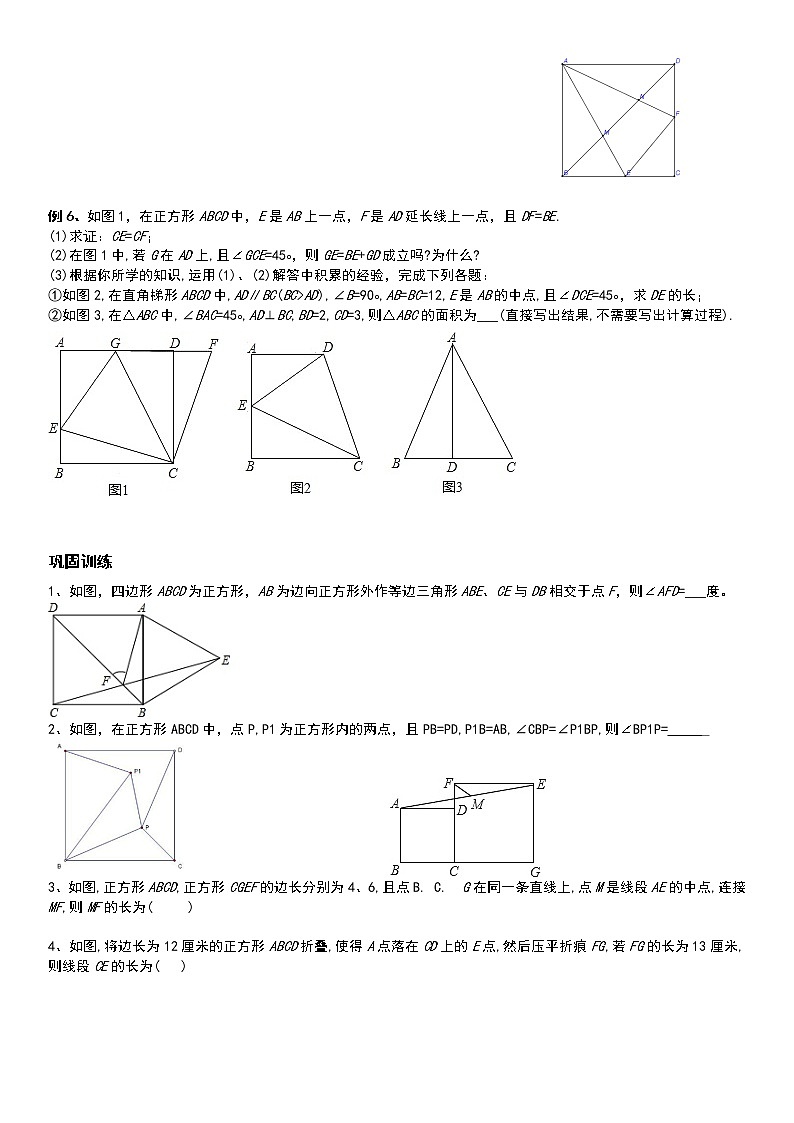
知识简述正方形作为完美的图形，既反映了特殊四边形的所有特征，又能与图形变换等重要的几何方法融为一体。由于正方形与直角三角形联系在一起，所以解正方形相关问题时，常用到勾股定理，具有代数风格，体现了数形结合思想。熟悉以下基本图形、基本结论：典例精讲例1、如图,在直角梯形ABCD中,AB=BC=4,M为腰BC上一点,且△ADM为等边三角形,则S△CDM:S△ABM=___.例2、如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=，那么AC的长等于___.例3、如图，在正方形ABCD中，E是AD边的中点，BD与CE交于F点。试判断AF与BE有何位置关系，并说明你的理由。例4、如图，正方形ABCD中，E为CD的中点，F是DA的中点，连接BE，与CF相交于P，求证：AP=AB. 例5、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,满足EF=BE+DF,AE、AF分别与对角线BD交于点M、N.求证:(1)∠EAF=45°;(2)MN=BM+DN                                                                          例6、如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.(1)求证：CE=CF；(2)在图1中,若G在AD上,且∠GCE=45∘，则GE=BE+GD成立吗?为什么?(3)根据你所学的知识,运用(1)、(2)解答中积累的经验，完成下列各题：①如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90∘,AB=BC=12,E是AB的中点,且∠DCE=45∘，求DE的长；②如图3,在△ABC中,∠BAC=45∘,AD⊥BC,BD=2,CD=3,则△ABC的面积为___(直接写出结果,不需要写出计算过程). 巩固训练1、如图，四边形ABCD为正方形，AB为边向正方形外作等边三角形ABE、CE与DB相交于点F，则∠AFD=___度。2、如图，在正方形ABCD中，点P,P1为正方形内的两点，且PB=PD,P1B=AB,∠CBP=∠P1BP,则∠BP1P=                               3、如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B. C. G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为(     ) 4、如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为(   )                                     5、如图,Rt△ABC中,∠C=90∘,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6，则另一直角边BC的长为___. 6、如图,四边形ABCD是正方形,直线l1,l2,l3分别通过A,B,C三点,且l1∥l2∥l3,若l1与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于(   )                              7、如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论：①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是         8、如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH.下列结论：①EG=DF;②∠AEH+∠ADH=180∘;③△EHF≌△DHC;④若AE/AB=2/3,则3S△EDH=13S△DHC，其中结论正确的有___.9、如图正方形ABCD的面积为64，三角形BCE是等边三角形，F是CE的中点，AE，BF交于点G，连接CG，则CG=___.                                            10、如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是              
      11、如图，四边形ABDE和ACFG都是正方形，过A作直线l，交BC，GE于M、N.                                                     求证：（1）AM=；（2）AN⊥GE；（3）EG+BC=2(AB+AC)         12、已知M、N分别为边长为1的正方形ABCD边CB、DC延长线上的点,且DN－BM＝MN． （1）如图1,求证：∠MAN＝45
（2）如图2,若DP⊥AN交AM于点P,求证：PA＋PC＝PD
（3）如图3,若C为DN的中点,求PC的长．