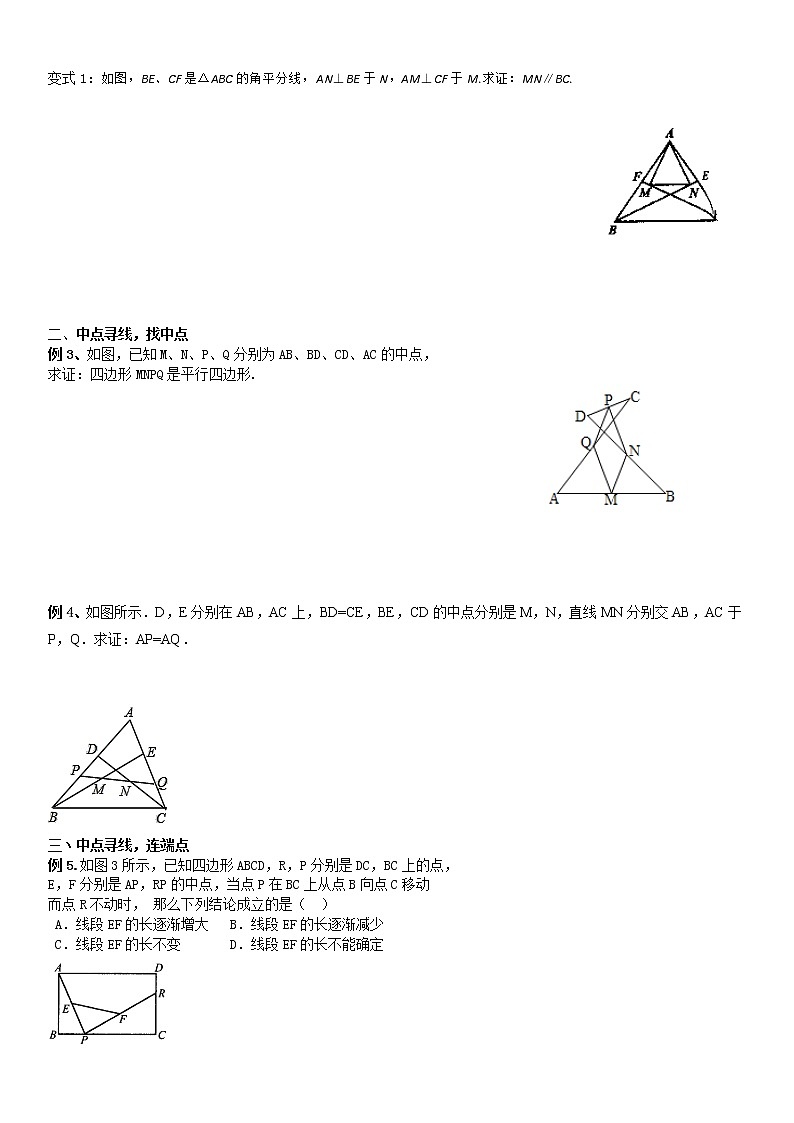
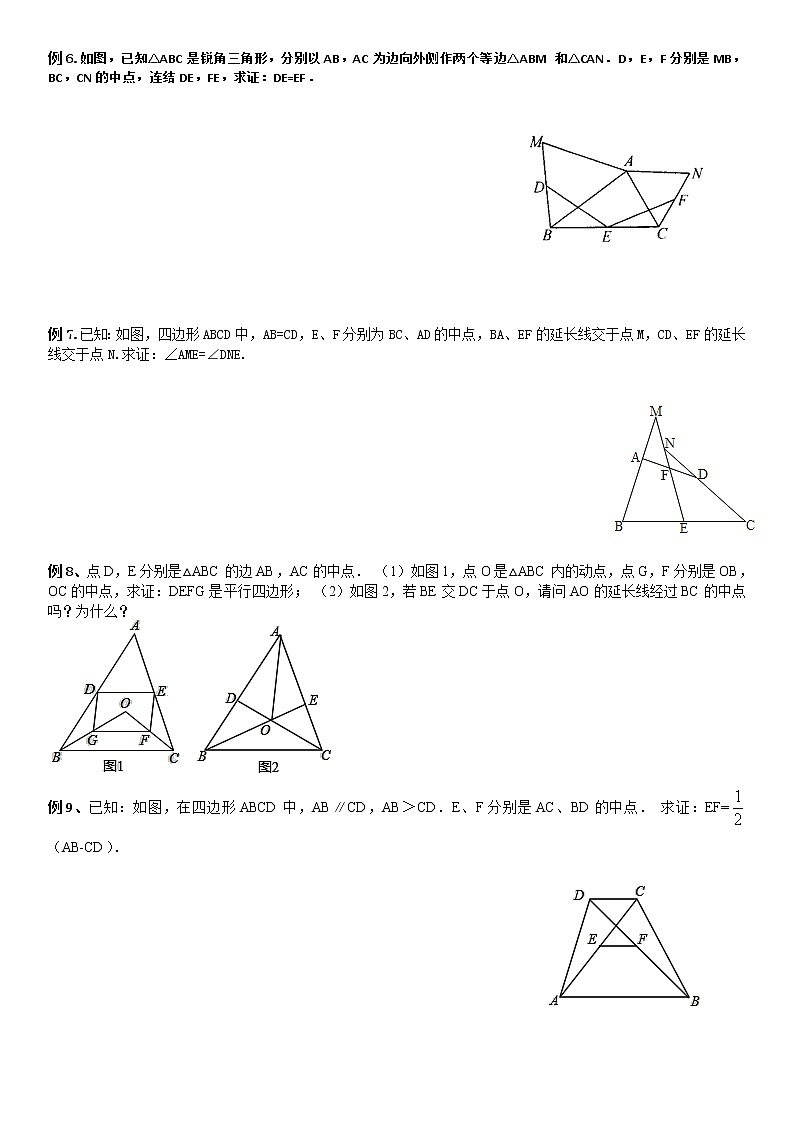
中位线（难）学案无答案

这是一份中位线（难）学案无答案，共11页。学案主要包含了知识梳理，典例精讲，巩固练习，课后作业等内容，欢迎下载使用。
【教学目标】1.探索并掌握三角形中位线的概念及性质。 2.会利用三角形中位线的性质解决相关问题。3.体会转化的思想方法。【知识梳理】一、与中点有关的概念三角形中线的定义：三角形顶点和对边中点的连线 三角形中线的相关定理： 直角三角形斜边的中线等于斜边的一半 等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．直角三角形斜边中线：直角三角形斜边中线等于斜边一半斜边中线判定：若三角形一边上的中线等于该边的一半，则这个三角形是直角三角形 【典例精讲】一丶角平分线的垂线必有等腰三角形例1、如图所示，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB=8，MN=3，则AC的长是（  ）A．12            B．14                 C．16               D．18      变式1：如图，在△ABC中，已知AB=6，AC=10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．        例2、如图，AD是△ABC的外角平分线，CD⊥AD于D，E是BC的中点. 求证：（1）DE∥AB； （2）DE=（AB+AC）      变式1：如图，BE、CF是△ABC的角平分线，AN⊥BE于N，AM⊥CF于M.求证：MN∥BC.           二、中点寻线，找中点例3、如图，已知M、N、P、Q分别为AB、BD、CD、AC的中点，求证：四边形MNPQ是平行四边形.          例4、如图所示．D，E分别在AB，AC上，BD=CE，BE，CD的中点分别是M，N，直线MN分别交AB，AC于P，Q．求证：AP=AQ．         三丶中点寻线，连端点例5.如图3所示，已知四边形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点B向点C移动而点R不动时， 那么下列结论成立的是（  ） A．线段EF的长逐渐增大   B．线段EF的长逐渐减少 C．线段EF的长不变       D．线段EF的长不能确定 例6.如图，已知△ABC是锐角三角形，分别以AB，AC为边向外侧作两个等边△ABM和△CAN．D，E，F分别是MB，BC，CN的中点，连结DE，FE，求证：DE=EF．           例7.已知：如图，四边形ABCD中，AB=CD，E、F分别为BC、AD的中点，BA、EF的延长线交于点M，CD、EF的延长线交于点N.求证：∠AME=∠DNE.          例8、点D，E分别是△ABC的边AB，AC的中点． （1）如图1，点O是△ABC内的动点，点G，F分别是OB，OC的中点，求证：DEFG是平行四边形； （2）如图2，若BE交DC于点O，请问AO的延长线经过BC的中点吗？为什么？       例9、已知：如图，在四边形ABCD中，AB∥CD，AB＞CD．E、F分别是AC、BD的中点． 求证：EF=（AB-CD）．           【巩固练习】1．如图，△ABC纸片中，AB=BC＞AC，点D是AB边的中点，点E在边AC上，将纸片沿DE折叠，使点A落在BC边上的点F处．则下列结论成立的个数有（　　）①△BDF是等腰直角三角形；②∠DFE=∠CFE；③DE是△ABC的中位线；④BF+CE=DF+DE．A．1个 B．2个 C．3个 D．4个2．在△ABC中，AB=12，AC=10，BC=9，AD是BC边上的高．将△ABC按如图所示的方式折叠，使点A与点D重合，折痕为EF，则△DEF的周长为（　　）A．9.5 B．10.5 C．11 D．15.53．如图所示，在△ABC中，AB=AC，M，N分别是AB，AC的中点，D，E为BC上的点，连接DN、EM，若AB=5cm，BC=8cm，DE=4cm，则图中阴影部分的面积为（　　）A．1cm2 B．1.5cm2 C．2cm2 D．3cm2 4．如图，将非等腰△ABC的纸片沿DE折叠后，使点A落在BC边上的点F处．若点D为AB边的中点，则下列结论：①△BDF是等腰三角形；②∠DFE=∠CFE；③DE是△ABC的中位线，成立的有（　　）A．①② B．①③ C．②③ D．①②③ 5．如图，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，且AB=6，BC=10，MN=1.5，则△ABC的周长是（　　）A．28 B．32 C．18 D．256．如图，沿Rt△ABC的中位线DE剪切一刀后，用得到的△ADE和四边形DBCE拼图，下列图形中不一定能拼出的是（　　）A．平行四边形 B．矩形 C．菱形 D．等腰梯形7．如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则S△DMN：S四边形ANME等于（　　）A．1：5 B．1：4 C．2：5 D．2：78．如图，在钝角△ABC中，点D，E分别是边AC，BC的中点，且DA=DE，那么下列结论错误的是（　　）A．∠1=∠2 B．∠1=∠3 C．∠B=∠C D．∠3=∠B9．如图，在等边△ABC中，M、N分别是边AB，AC的中点，D为MN上任意一点，BD，CD的延长线分别交于AB，AC于点E，F．若=6，则△ABC的边长为（　　）A． B． C． D．110．已知：四边形ABCD中，AB=2，CD=3，M、N分别是AD，BC的中点，则线段MN的取值范围是（　　）A．1＜MN＜5 B．1＜MN≤5 C．＜MN＜ D．＜MN≤11．如图，在△ABC中，M为BC中点，AN平分∠BAC，AN⊥BN于N，且AB=10，AC=16，则MN等于（　　）A．2 B．2.5 C．3 D．3.5    12．如图，已知AB=10，P是线段AB上的动点，分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB，连接CD，设CD的中点为G，当点P从点A运动到点B时，则点G移动路径的长是　   　．   13．如图，有一块直角三角形的木板AOB，∠O=90°，OA=3，OB=4，一只小蚂蚁在OA边上爬行（可以与O、A重合），设其所处的位置C到AB的中点D的距离为x，则x的取值范围是　   　．  14．如图，在△ABC中，AB=AC．M、N分别是AB、AC的中点，D、E为BC上的点，连接DN、EM．若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面积为　   　cm2．  15．如图，顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形，再顺次连接所得的小三角形各边中点得到第2个小三角形，如此操作下去，则第n个小三角形的面积为　   　． 16．（1）证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半；[要求根据图1写出已知、求证、证明；在证明过程中，至少有两处写出推理依据（“已知”除外）]（2）如图2，在▱ABCD中，对角线交点为O，A1、B1、C1、D1分别是OA、OB、OC、OD的中点，A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点，…，以此类推．若▱ABCD的周长为1，直接用算式表示各四边形的周长之和l；（3）借助图形3反映的规律，猜猜l可能是多少？       17．如图，已知AE、BD相交于点C，AC=AD，BC=BE，F、G、H分别是DC、CE、AB的中点．求证：（1）HF=HG；（2）∠FHG=∠DAC．          【课后作业】 1．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠FPE=100°，则∠PFE的度数是　   　． 2．如图，在△ABC中，∠ACB=90°，点D，E，F分别是AB，BC，CA的中点，若CD=2，则线段EF的长是　   　．3．在△ABC中，AB=6，点D是AB的中点，过点D作DE∥BC，交AC于点E，点M在DE上，且ME=DM．当AM⊥BM时，则BC的长为　   　．4．如图，Rt△ABC中，∠ACB=90°，AB=6，点D是AB的中点，过AC的中点E作EF∥CD交AB于点F，则EF=　   　． 5．如图，∠ACB=90°，D为AB中点，连接DC并延长到点E，使CE=CD，过点B作BF∥DE交AE的延长线于点F．若BF=10，则AB的长为　   　．  6．如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=BD，连接DM、DN、MN．若AB=6，则DN=　   　．     7．已知：△ABC中，AB=10．（1）如图①，若点D、E分别是AC、BC边的中点，求DE的长；（2）如图②，若点A1，A2把AC边三等分，过A1，A2作AB边的平行线，分别交BC边于点B1，B2，求A1B1+A2B2的值；（3）如图③，若点A1，A2，…，A10把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B1，B2，…B10．根据你所发现的规律，直接写出A1B1+A2B2+…+A10B10的结果． 8.在△ABC外作正方形ACDE和ABGF.M是BC的中点，O1、O2分别是正方形的中心.   求证：（1）MO1=MO2；                   （2）MO1⊥MO2.           9. 如图，P为△ABC内一点，∠PAC=∠PBC，PM⊥AC于M，PN⊥BC于N.D是AB的中点.求证：DM=DN            10.如图，△ABC中，M是AB的中点，P是AC的中点，D是MB的中点，N是CD的中点，Q是MN的中点，直线PQ交MB于K。求证：K是DB的中点。