
2021-2022学年四川省德阳市中考数学模拟试题含解析
展开2021-2022中考数学模拟试卷
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.如图,将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,连接AA',若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
2.如图,嘉淇同学拿20元钱正在和售货员对话,且一本笔记本比一支笔贵3元,请你仔细看图,1本笔记本和1支笔的单价分别为( )
A.5元,2元 B.2元,5元
C.4.5元,1.5元 D.5.5元,2.5元
3.已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
A.3:2 B.9:4 C.2:3 D.4:9
4.若a+|a|=0,则等于( )
A.2﹣2a B.2a﹣2 C.﹣2 D.2
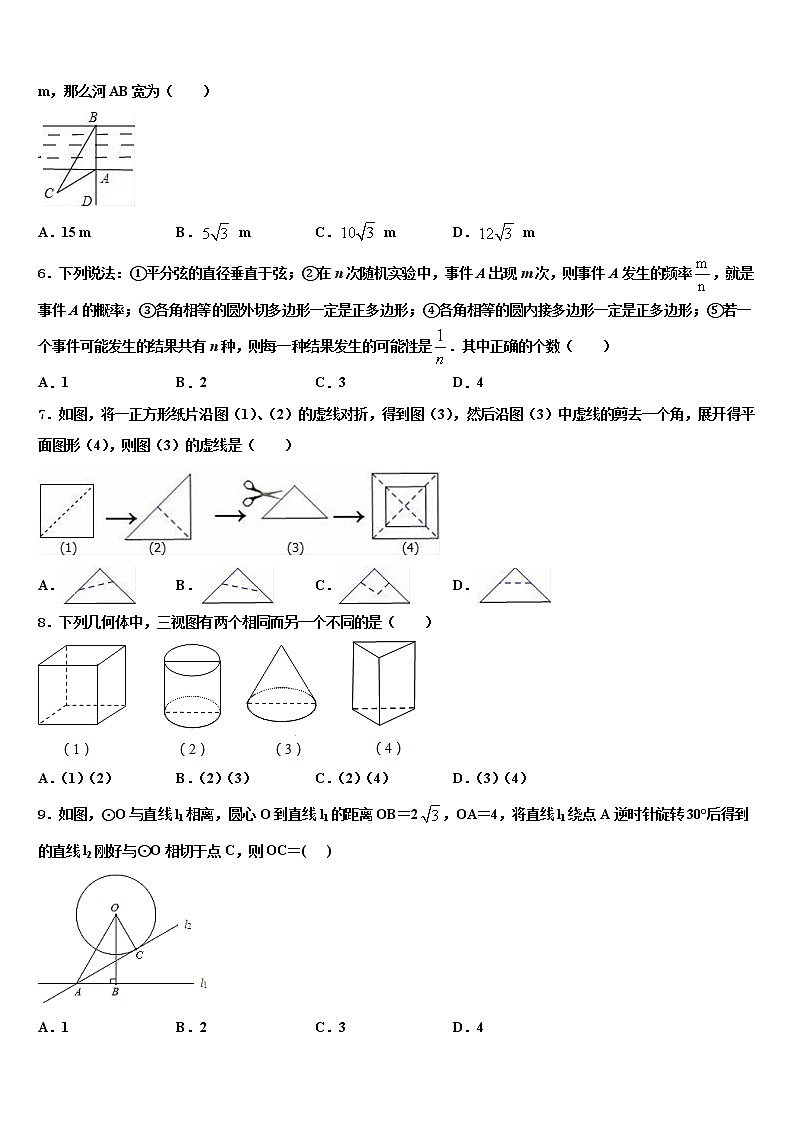
5.如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15 m,那么河AB宽为( )
A.15 m B. m C. m D. m
6.下列说法:①平分弦的直径垂直于弦;②在n次随机实验中,事件A出现m次,则事件A发生的频率,就是事件A的概率;③各角相等的圆外切多边形一定是正多边形;④各角相等的圆内接多边形一定是正多边形;⑤若一个事件可能发生的结果共有n种,则每一种结果发生的可能性是.其中正确的个数( )
A.1 B.2 C.3 D.4
7.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
A. B. C. D.
8.下列几何体中,三视图有两个相同而另一个不同的是( )
A.(1)(2) B.(2)(3) C.(2)(4) D.(3)(4)
9.如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=( )
A.1 B.2 C.3 D.4
10.据浙江省统计局发布的数据显示,2017年末,全省常住人口为5657万人数据“5657万”用科学记数法表示为
A. B. C. D.
11.的倒数的绝对值是( )
A. B. C. D.
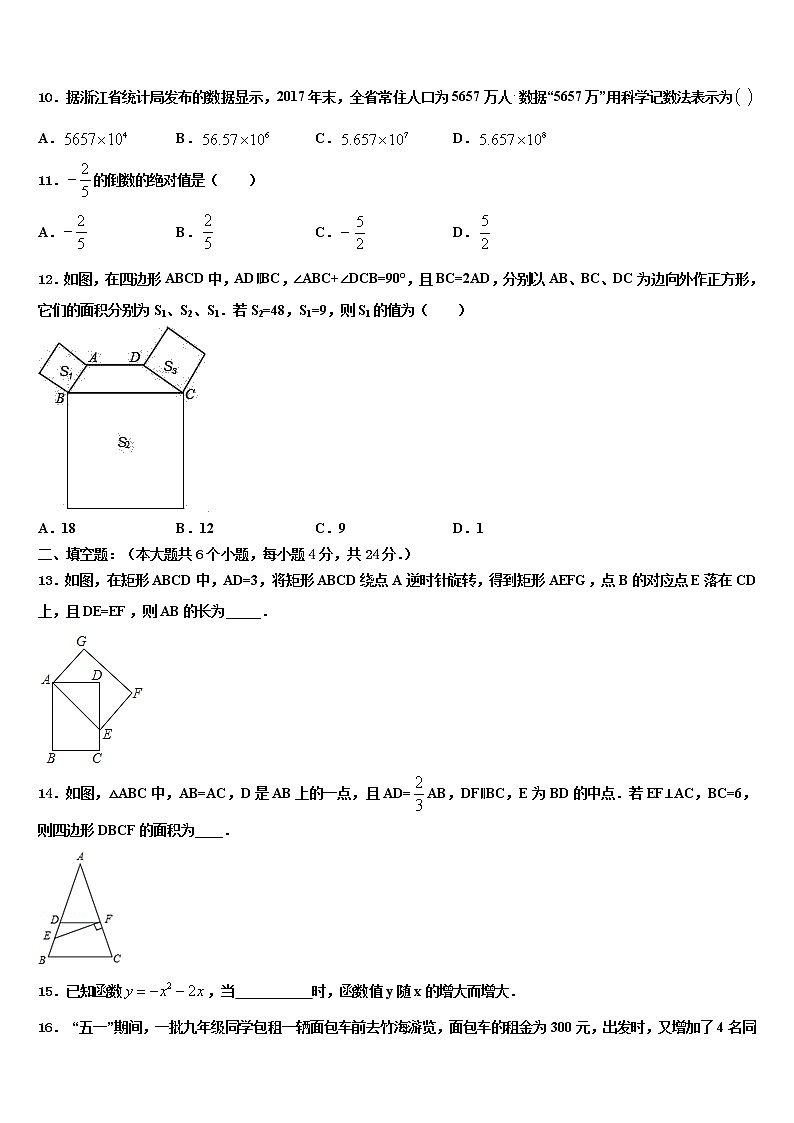
12.如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S1.若S2=48,S1=9,则S1的值为( )
A.18 B.12 C.9 D.1
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.
14.如图,△ABC中,AB=AC,D是AB上的一点,且AD=AB,DF∥BC,E为BD的中点.若EF⊥AC,BC=6,则四边形DBCF的面积为____.
15.已知函数,当 时,函数值y随x的增大而增大.
16. “五一”期间,一批九年级同学包租一辆面包车前去竹海游览,面包车的租金为300元,出发时,又增加了4名同学,且租金不变,这样每个同学比原来少分摊了20元车费.若设参加游览的同学一共有x人,为求x,可列方程_____.
17.中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为_____.
18.已知一个多边形的每一个外角都等于,则这个多边形的边数是 .
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19.(6分)在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的表达式;
(2)在x轴上有一点D(-4,0),将二次函数的图象沿射线DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②直接写出此二次函数的图象在A,B两点之间(含A,B两点)的曲线部分在平移过程中所扫过的面积.
20.(6分)如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
21.(6分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.求证:△BDE≌△BCE;试判断四边形ABED的形状,并说明理由.
22.(8分)若关于的方程无解,求的值.
23.(8分)已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求的长.
24.(10分)列方程或方程组解应用题:
去年暑期,某地由于暴雨导致电路中断,该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,10分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求吉普车的速度.
25.(10分)计算:|-2|+2﹣1﹣cos61°﹣(1﹣)1.
26.(12分)如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
若AC=4,BC=2,求OE的长.试判断∠A与∠CDE的数量关系,并说明理由.
27.(12分)为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(1)本次抽测的男生人数为 ,图①中m的值为 ;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
参考答案
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、B
【解析】
根据图形旋转的性质得AC=A′C,∠ACA′=90°,∠B=∠A′B′C,从而得∠AA′C=45°,结合∠1=20°,即可求解.
【详解】
∵将RtABC绕直角项点C顺时针旋转90°,得到A' B'C,
∴AC=A′C,∠ACA′=90°,∠B=∠A′B′C,
∴∠AA′C=45°,
∵∠1=20°,
∴∠B′A′C=45°-20°=25°,
∴∠A′B′C=90°-25°=65°,
∴∠B=65°.
故选B.
【点睛】
本题主要考查旋转的性质,等腰三角形和直角三角形的性质,掌握等腰三角形和直角三角形的性质定理,是解题的关键.
2、A
【解析】
可设1本笔记本的单价为x元,1支笔的单价为y元,由题意可得等量关系:①3本笔记本的费用+2支笔的费用=19元,②1本笔记本的费用﹣1支笔的费用=3元,根据等量关系列出方程组,再求解即可.
【详解】
设1本笔记本的单价为x元,1支笔的单价为y元,依题意有:
,解得:.
故1本笔记本的单价为5元,1支笔的单价为2元.
故选A.
【点睛】
本题考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系设出未知数,列出方程组.
3、A
【解析】
试题解析:过点D作DE⊥AB于E,DF⊥AC于F.
∵AD为∠BAC的平分线,
∴DE=DF,又AB:AC=3:2,
故选A.
点睛:角平分线上的点到角两边的距离相等.
4、A
【解析】
直接利用二次根式的性质化简得出答案.
【详解】
∵a+|a|=0,
∴|a|=-a,
则a≤0,
故原式=2-a-a=2-2a.
故选A.
【点睛】
此题主要考查了二次根式的性质与化简,正确化简二次根式是解题关键.
5、A
【解析】
过C作CE⊥AB,
Rt△ACE中,
∵∠CAD=60°,AC=15m,
∴∠ACE=30°,AE=AC=×15=7.5m,CE=AC•cos30°=15×=,
∵∠BAC=30°,∠ACE=30°,
∴∠BCE=60°,
∴BE=CE•tan60°=×=22.5m,
∴AB=BE﹣AE=22.5﹣7.5=15m,
故选A.
【点睛】本题考查的知识点是解直角三角形的应用,关键是构建直角三角形,解直角三角形求出答案.
6、A
【解析】
根据垂径定理、频率估计概率、圆的内接多边形、外切多边形的性质与正多边形的定义、概率的意义逐一判断可得.
【详解】
①平分弦(不是直径)的直径垂直于弦,故此结论错误;
②在n次随机实验中,事件A出现m次,则事件A发生的频率,试验次数足够大时可近似地看做事件A的概率,故此结论错误;
③各角相等的圆外切多边形是正多边形,此结论正确;
④各角相等的圆内接多边形不一定是正多边形,如圆内接矩形,各角相等,但不是正多边形,故此结论错误;
⑤若一个事件可能发生的结果共有n种,再每种结果发生的可能性相同是,每一种结果发生的可能性是.故此结论错误;
故选:A.
【点睛】
本题主要考查命题的真假,解题的关键是掌握垂径定理、频率估计概率、圆的内接多边形、外切多边形的性质与正多边形的定义、概率的意义.
7、D
【解析】
本题关键是正确分析出所剪时的虚线与正方形纸片的边平行.
【详解】
要想得到平面图形(4),需要注意(4)中内部的矩形与原来的正方形纸片的边平行,故剪时,虚线也与正方形纸片的边平行,所以D是正确答案,故本题正确答案为D选项.
【点睛】
本题考查了平面图形在实际生活中的应用,有良好的空间想象能力过动手能力是解题关键.
8、B
【解析】
根据三视图的定义即可解答.
【详解】
正方体的三视图都是正方形,故(1)不符合题意;
圆柱的主视图、左视图都是矩形,俯视图是圆,故(2)符合题意;
圆锥的主视图、左视图都是三角形,俯视图是圆形,故(3)符合题意;
三棱锥主视图是、左视图是,俯视图是三角形,故(4)不符合题意;
故选B.
【点睛】
本题考查了简单几何体的三视图,熟知三视图的定义是解决问题的关键.
9、B
【解析】
先利用三角函数计算出∠OAB=60°,再根据旋转的性质得∠CAB=30°,根据切线的性质得OC⊥AC,从而得到∠OAC=30°,然后根据含30度的直角三角形三边的关系可得到OC的长.
【详解】
解:在Rt△ABO中,sin∠OAB===,
∴∠OAB=60°,
∵直线l1绕点A逆时针旋转30°后得到的直线l1刚好与⊙O相切于点C,
∴∠CAB=30°,OC⊥AC,
∴∠OAC=60°﹣30°=30°,
在Rt△OAC中,OC=OA=1.
故选B.
【点睛】
本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交⇔d<r;直线l和⊙O相切⇔d=r;直线l和⊙O相离⇔d>r.也考查了旋转的性质.
10、C
【解析】
科学记数法的表示形式为的形式,其中,n为整数确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同当原数绝对值时,n是正数;当原数的绝对值时,n是负数.
【详解】
解:5657万用科学记数法表示为,
故选:C.
【点睛】
此题考查科学记数法的表示方法科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.
11、D
【解析】
直接利用倒数的定义结合绝对值的性质分析得出答案.
【详解】
解:−的倒数为−,则−的绝对值是:.
故答案选:D.
【点睛】
本题考查了倒数的定义与绝对值的性质,解题的关键是熟练的掌握倒数的定义与绝对值的性质.
12、D
【解析】
过A作AH∥CD交BC于H,根据题意得到∠BAE=90°,根据勾股定理计算即可.
【详解】
∵S2=48,∴BC=4,过A作AH∥CD交BC于H,则∠AHB=∠DCB.
∵AD∥BC,∴四边形AHCD是平行四边形,∴CH=BH=AD=2,AH=CD=1.
∵∠ABC+∠DCB=90°,∴∠AHB+∠ABC=90°,∴∠BAH=90°,∴AB2=BH2﹣AH2=1,∴S1=1.
故选D.
【点睛】
本题考查了勾股定理,正方形的性质,平行四边形的判定和性质,正确的作出辅助线是解题的关键.
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13、3
【解析】
【分析】根据旋转的性质知AB=AE,在直角三角形ADE中根据勾股定理求得AE长即可得.
【详解】∵四边形ABCD是矩形,∴∠D=90°,BC=AD=3,
∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG,
∴EF=BC=3,AE=AB,
∵DE=EF,
∴AD=DE=3,
∴AE==3,
∴AB=3,
故答案为3.
【点睛】本题考查矩形的性质和旋转的性质,熟知旋转前后哪些线段是相等的是解题的关键.
14、2
【解析】
解:如图,过D点作DG⊥AC,垂足为G,过A点作AH⊥BC,垂足为H,
∵AB=AC,点E为BD的中点,且AD=AB,
∴设BE=DE=x,则AD=AF=1x.
∵DG⊥AC,EF⊥AC,
∴DG∥EF,∴,即,解得.
∵DF∥BC,∴△ADF∽△ABC,∴,即,解得DF=1.
又∵DF∥BC,∴∠DFG=∠C,
∴Rt△DFG∽Rt△ACH,∴,即,解得.
在Rt△ABH中,由勾股定理,得.
∴.
又∵△ADF∽△ABC,∴,
∴
∴.
故答案为:2.
15、x≤﹣1.
【解析】
试题分析:∵=,a=﹣1<0,抛物线开口向下,对称轴为直线x=﹣1,∴当x≤﹣1时,y随x的增大而增大,故答案为x≤﹣1.
考点:二次函数的性质.
16、 ﹣=1.
【解析】
原有的同学每人分担的车费应该为,而实际每人分担的车费为,方程应该表示为:﹣=1.
故答案是:﹣=1.
17、
【解析】
试题分析:根据有理数的加法,可得图②中表示(+2)+(﹣5)=﹣1,
故答案为﹣1.
考点:正数和负数
18、5
【解析】
∵多边形的每个外角都等于72°,
∵多边形的外角和为360°,
∴360°÷72°=5,
∴这个多边形的边数为5.
故答案为5.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19、(1)y=﹣x2+4;(2)①E(5,9);②1.
【解析】
(1)待定系数法即可解题,
(2)①求出直线DA的解析式,根据顶点E在直线DA上,设出E的坐标,带入即可求解;②AB扫过的面积是平行四边形ABGE,根据S四边形ABGE=S矩形IOKH﹣S△AOB﹣S△AEI﹣S△EHG﹣S△GBK,求出点B(2,0),G(7,5),A(0,4),E(5,9),根据坐标几何含义即可解题.
【详解】
解:(1)∵A(0,4),B(2,0),C(﹣2,0)
∴二次函数的图象的顶点为A(0,4),
∴设二次函数表达式为y=ax2+4,
将B(2,0)代入,得4a+4=0,
解得,a=﹣1,
∴二次函数表达式y=﹣x2+4;
(2)①设直线DA:y=kx+b(k≠0),
将A(0,4),D(﹣4,0)代入,得 ,
解得, ,
∴直线DA:y=x+4,
由题意可知,平移后的抛物线的顶点E在直线DA上,
∴设顶点E(m,m+4),
∴平移后的抛物线表达式为y=﹣(x﹣m)2+m+4,
又∵平移后的抛物线过点B(2,0),
∴将其代入得,﹣(2﹣m)2+m+4=0,
解得,m1=5,m2=0(不合题意,舍去),
∴顶点E(5,9),
②如图,连接AB,过点B作BL∥AD交平移后的抛物线于点G,连结EG,
∴四边形ABGE的面积就是图象A,B两点间的部分扫过的面积,
过点G作GK⊥x轴于点K,过点E作EI⊥y轴于点I,直线EI,GK交于点H.
由点A(0,4)平移至点E(5,9),可知点B先向右平移5个单位,再向上平移5个单位至点G.
∵B(2,0),∴点G(7,5),
∴GK=5,OB=2,OK=7,
∴BK=OK﹣OB=7﹣2=5,
∵A(0,4),E(5,9),
∴AI=9﹣4=5,EI=5,
∴EH=7﹣5=2,HG=9﹣5=4,
∴S四边形ABGE=S矩形IOKH﹣S△AOB﹣S△AEI﹣S△EHG﹣S△GBK
=7×9﹣×2×4﹣×5×5﹣×2×4﹣×5×5
=63﹣8﹣25
=1
答:图象A,B两点间的部分扫过的面积为1.
【点睛】
本题考查了二次函数解析式的求法,二次函数的图形和性质,二次函数的实际应用,难度较大,建立面积之间的等量关系是解题关键.
20、(1)证明见解析;(2).
【解析】
试题分析:(1)连接OP,首先证明OP∥BC,推出∠OPB=∠PBC,由OP=OB,推出∠OPB=∠OBP,由此推出∠PBC=∠OBP;
(2)作PH⊥AB于H.首先证明PC=PH=1,在Rt△APH中,求出AH,由△APH∽△ABC,求出AB、BH,由Rt△PBC≌Rt△PBH,推出BC=BH即可解决问题.
试题解析:
(1)连接OP,
∵AC是⊙O的切线,
∴OP⊥AC,
∴∠APO=∠ACB=90°,
∴OP∥BC,
∴∠OPB=∠PBC,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠PBC=∠OBP,
∴BP平分∠ABC;
(2)作PH⊥AB于H.则∠AHP=∠BHP=∠ACB=90°,
又∵∠PBC=∠OBP,PB=PB,
∴△PBC≌△PBH ,
∴PC=PH=1,BC=BH,
在Rt△APH中,AH=,
在Rt△ACB中,AC2+BC2=AB2
∴(AP+PC)2+BC2=(AH+HB)2,
即42+BC2=(+BC)2,
解得.
21、证明见解析.
【解析】
(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
【详解】
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴BA=BE=ED= AD
∴四边形ABED为菱形.
考点:旋转的性质;全等三角形的判定与性质;菱形的判定.
22、
【解析】
分析:该分式方程无解的情况有两种:(1)原方程存在增根;(2)原方程约去分母后,整式方程无解.
详解:去分母得:x(x-a)-1(x-1)=x(x-1),
去括号得:x2-ax-1x+1=x2-x,
移项合并得:(a+2)x=1.
(1)把x=0代入(a+2)x=1,
∴a无解;
把x=1代入(a+2)x=1,
解得a=1;
(2)(a+2)x=1,
当a+2=0时,0×x=1,x无解
即a=-2时,整式方程无解.
综上所述,当a=1或a=-2时,原方程无解.
故答案为a=1或a=-2.
点睛:分式方程无解,既要考虑分式方程有增根的情形,又要考虑整式方程无解的情形.
23、 (1)见解析;(2).
【解析】
(1)先证明△OAC≌△ODC,得出∠1=∠2,则∠2=∠4,故OC∥DE,即可证得DE⊥CF;
(2)根据OA=OC得到∠2=∠3=30°,故∠COD=120°,再根据弧长公式计算即可.
【详解】
解:(1)DE⊥CF.
理由如下:
∵CF为切线,
∴OC⊥CF,
∵CA=CD,OA=OD,OC=OC,
∴△OAC≌△ODC,
∴∠1=∠2,
而∠A=∠4,
∴∠2=∠4,
∴OC∥DE,
∴DE⊥CF;
(2)∵OA=OC,
∴∠1=∠A=30°,
∴∠2=∠3=30°,
∴∠COD=120°,
∴.
【点睛】
本题考查了全等三角形的判定与性质与弧长的计算,解题的关键是熟练的掌握全等三角形的判定与性质与弧长的公式.
24、吉普车的速度为30千米/时.
【解析】
先设抢修车的速度为x千米/时,则吉普车的速度为1.5x千米/时,列出方程求出x的值,再进行检验,即可求出答案.
【详解】
解:设抢修车的速度为x千米/时,则吉普车的速度为15x千米/时.
由题意得:.
解得,x=20
经检验,x=20是原方程的解,并且x=20,1.5x=30都符合题意.
答:吉普车的速度为30千米/时.
点评:本题难度中等,主要考查学生对分式方程实际应用的综合运用.为中考常见题型,要求学生牢固掌握.注意检验.
25、1-
【解析】
利用零指数幂和绝对值的性质、特殊角的三角函数值、负指数次幂的性质进行计算即可.
【详解】
解:原式=.
【点睛】
本题考查了零指数幂和绝对值的性质、特殊角的三角函数值、负指数次幂的性质,熟练掌握性质及定义是解题的关键.
26、(1);(2)∠CDE=2∠A.
【解析】
(1)在Rt△ABC中,由勾股定理得到AB的长,从而得到半径AO .再由△AOE∽△ACB,得到OE的长;
(2)连结OC,得到∠1=∠A,再证∠3=∠CDE,从而得到结论.
【详解】
(1)∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,由勾股定理得:
AB=
=,
∴AO=AB=.
∵OD⊥AB,
∴∠AOE=∠ACB=90°,
又∵∠A=∠A,
∴△AOE∽△ACB,
∴,
∴OE=
=.
(2)∠CDE=2∠A.理由如下:
连结OC,
∵OA=OC,
∴∠1=∠A,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠2+∠CDE=90°,
∵OD⊥AB,
∴∠2+∠3=90°,
∴∠3=∠CDE.
∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.
考点:切线的性质;探究型;和差倍分.
27、(1)50、1;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有2人体能达标.
【解析】
分析:(Ⅰ)根据4次的人数及其百分比可得总人数,用6次的人数除以总人数求得m即可;
(Ⅱ)根据平均数、众数、中位数的定义求解可得;
(Ⅲ)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得.
详解:(Ⅰ)本次抽测的男生人数为10÷20%=50,m%=×100%=1%,所以m=1.
故答案为50、1;
(Ⅱ)平均数为=5.16次,众数为5次,中位数为=5次;
(Ⅲ)×350=2.
答:估计该校350名九年级男生中有2人体能达标.
点睛:本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
2024年四川省德阳市中考一诊模拟数学模拟预测题(含解析): 这是一份2024年四川省德阳市中考一诊模拟数学模拟预测题(含解析),共34页。试卷主要包含了已知的相反数是,则的值是,下列计算正确的是,已知某几何体的三视图等内容,欢迎下载使用。
四川省资阳市雁江区2021-2022学年中考数学模拟试题含解析: 这是一份四川省资阳市雁江区2021-2022学年中考数学模拟试题含解析,共20页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
四川省德阳市中学江县2021-2022学年中考联考数学试卷含解析: 这是一份四川省德阳市中学江县2021-2022学年中考联考数学试卷含解析,共20页。












