三角函数4三角函数求锐角和特殊角学案-无答案

这是一份三角函数4三角函数求锐角和特殊角学案-无答案，共9页。学案主要包含了新课，随堂练习，选择题，课后总结等内容，欢迎下载使用。
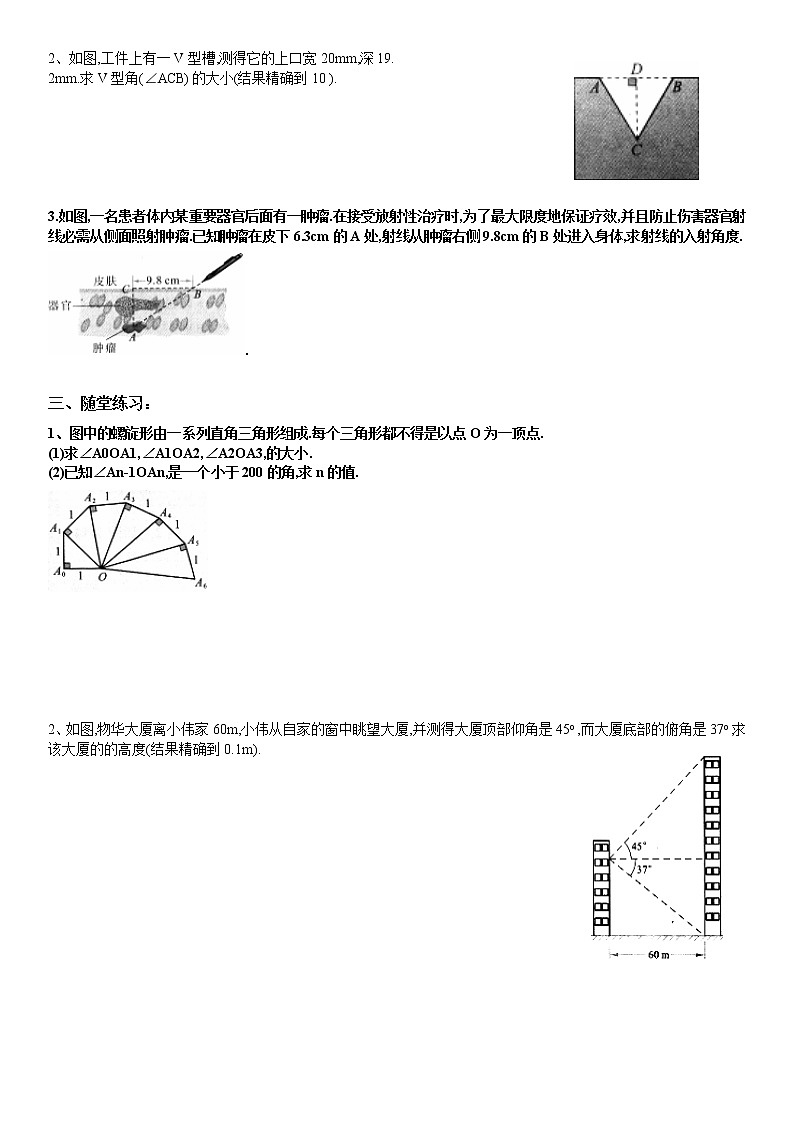
由三角函数求锐角和特殊角的三角函数一、教学目的1.经历用计算器由三角函数值求相应锐角的过程，进一步体会三角函数的意义.2.能够利用计算器进行有关三角函数值的计算.3.能够运用计算器辅助解决含三角函数值计算的实际问题.使学生理角三角形        4、通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、5、渗透数形结合的数学思想，培养学生良好的学习习惯．重点与难点：重点：直角三角形的解法．难点：用计算器辅助解决含三角函数值计算的实际问题.三角函数在解直角三角形中的灵活运用．用计算器由已知三角函数值求锐角.能够用计算器辅助解决含三角函数值计算的实际问题.二、知识梳理已知平顶屋面的宽度L和坡顶的设计高度h（如图）。你能求出斜面钢条的长度和倾角a 吗？  变：已知平顶屋面的宽度L和坡顶的设计倾角α（如图）。你能求出斜面钢条的长度和设计高度h吗？        二、新课1、像这样，在直角三角形中，由已知的一些边、角，求出另一些边、角的过程，叫做解直角三角形.在三角形中共有几个元素？直角三角形ABC中，∠C=90°，a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？ (1)三边之间关系：a2  +b2  =c2 (勾股定理) (2)锐角之间关系∠A+∠B=90°．(3)边角之间关系       三、典例精讲由三角函数求锐角一、   复习特殊角的三角函数值。       三角函数值的逆运算的复习。（用相似稍微说明锐角的唯一性）二、   引入：若不是特殊角呢？比如32°sin32°你知道是多少吗？（计算器）练习： (1)sin56°；(2)sin15°49′； (3)cos20°；(4)tan29°； (5)tan44°59′59″；(6)sin15°+cos61°+tan76°.(1)≈0.8290； (2)≈0.2726； (3)≈0.9397；(4)≈0.5543； (5)″≈1.0000；(6)≈0.2588+0.4848+4.0108=4.7544.(1)sin15°+sin25°＝sin40°(2)cos20°+cos26°=cos46°(3)tan25°+tan15°＝tan40°(1)sin15°+sin25°≈0.2588+0.4226＝0.6814；sin40°≈0.6428，∴sin15°+sin25°≠sin40°； (2)cos20°+cos26°≈0.9397+0.8988＝1.8385。cos46°≈0.6947，∴cos20°+cos26°≠cos46°； (3)tan25°+tan15°≈0.4663+0.2679＝0.7342，tan40°≈0.8391，∴tan25°+tan15°≠tan40°. 应用：如图，当登山缆车的吊箱经过点A到达点B时，它走过了200米，已知缆车行驶的路线与水平面的夹角为∠a＝16°，那么缆车垂直上升的距离是多少?sin16°=,∴BC＝ABsin16°＝200 sin16°(米).反之，若已知sinA=0.1234，你知道∠A的值是多少吗？学习计算器求锐角：练习：已知sinA=0.9816，求锐角A，已知cosA＝0.8607，求锐角A；已知tanA=0.1890，求锐角A；已知tanA＝56.78，求锐角A. 练习：根据下列条件求锐角θ的大小：(1)  tanθ＝2.9888；(2)sinθ=0.3957；（3）cosθ＝0.7850；(4)tanθ＝0.8972；(5)sinθ＝；(6)cosθ＝； (7)tanθ=；   经典例题：1、如图,为了方便行人，市政府在10m高的天桥.两端修建了40m长的斜道.这条斜道的倾斜角是多少?      2、如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).      3.如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度.. 三、随堂练习：1、图中的螺旋形由一系列直角三角形组成.每个三角形都不得是以点O为一顶点.(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小.(2)已知∠An-1OAn,是一个小于200的角,求n的值.      2、如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是45o ,而大厦底部的俯角是37o ,求该大厦的的高度(结果精确到0.1m).             由三角函数求锐角练习 特殊角的三角函数例1在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B, ∠C的对边.解下列直角三角形(1)  已知a=3,b=3,                   (2)已知c=8,b=4,               (3)已知c=8,∠A=450,    强调与说明：解直角三角形，只有下面两种情况：  （1）已知两条边；（2）已知一条边和一个锐角   （两个已知元素中至少有一条边）问题分类：解直角三角形：(如图)在⊿ABC中，∠C=900，（1）.已知a,b.解直角三角形(即求：∠A，∠B及C边)（2）. 已知∠A，a.解直角三角形（3）.已知∠A，b. 解直角三角形（4） 已知∠A，c. 解直角三角形    例2 如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A=26º,求中柱BC（C为底边中点）和上弦AB的长（精确到0.01米）tan26º=0.4877,cos26º=0.8988)      例3  为测量松树AB的高度，一个人站在距松树15米的E处，测得仰角∠ACD=52º,已知人的高度是1.72米，求树高（精确到0.01米）（tg52º=1.2799）练习A类1、在下列直角三角形中不能求解的是（  ）A、已知一直角边一锐角           B、已知一斜边一锐角C、已知两边                     D、已知两角2. 已知：在Rt△ABC中，∠C=90，b=2√3,c=4.求:(1)a=                 (2) ∠B=               ∠A=  3   解直角三角形在Rt△ABC中      B类4：在Rt△ABC中，∠C=90°， ∠A=50 °，AB=3。求∠B和a，b（边长保留2个有效数字）    5：（引入题中）已知平顶屋面的宽度L为10m，坡顶的设计高度h为3.5m，（或设计倾角a ）（如图）。你能求出斜面钢条的长度和倾角a。(长度精确到0.1米,角度精确到1度)     C类 5如图，两建筑物的水平距离BC为24米，从点A测得点D的俯角a＝300测得点C的俯角    ＝60°，求AB和CD两座建筑物的高．（结果保留根号）      四、巩固练习解直角三角形作业（一）1、由下列条件解题：在Rt△ABC中，∠C=90°：（1）已知a=4，b=8，求c．   （2）已知b=10，∠B=60°，求a，c．    （3）已知c=20，∠A=60°，求a，b．   2、已知等腰△ABC中，AB=AC=13，BC=10，求顶角∠A的四种三角函数值．    3、在△ABC中，∠C＝90°，，求∠A、∠B、c边.   解直角三角形作业（二）1、一坡面的坡角为600，则坡度i=            ；2、在Rt△ABC中，∠C=900，∠A=300，b=，则a=        ，c=         ；3、已知在直角梯形ABCD中，上底CD=4，下底AB=10，非直角腰BC=，则底角∠B=     ；4、若∠A是锐角，且cosA=，则cos（900-A）=            ；5、如图，塔AB和楼CD的水平距离为80m，从楼顶C处及楼底D处测得塔顶A的仰角分别为450和600，试求塔高和楼高。      6、去年某省将地处A、B两地的两所大学合并成一所综合性大学，为了方便两地师生交往，学校准备在相距2km的A、B两地之间修一条笔直的公路，经测量在A地北偏东600方向，B地北偏西450方向的C处有一个半径为0.7km的公园，问计划修筑的这条公路会不会穿过公园？为什么？     解直角三角形作业（三）1、若∠A是锐角，且cosA=sinA，则∠A的度数是（      ）  A、300         B、450        C、600        D、不能确定2、如图，梯形ABCD中，AD∥BC，∠B=450，∠C=1200，AB=8，则CD的长为（    ）  A、        B、           C、         D、3、在Rt△ABC中，∠C=900，AB=2AC，在BC上取一点D，使AC=CD，则CD：BD=（     ）  A、        B、         C、         D、不能确定4、在Rt△ABC中，∠C=900，AC=1，sinA=，求tanA，BC。     5、在△ABC中，AD⊥BC，垂足为D，AB=，AC=BC=，求AD的长。     6、某市为加固长90米，高30米，坝顶宽为6米，迎水坡和背水坡都是1：1的横断面是梯形的防洪大坝，要将大坝加高2米，背水坡坡度改为1：1.5，已知坝顶宽不变，求大坝横截面积增加多少平方米。       五、拓展提升一、选择题（每题5分，共25分）1．在Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，则下列结论成立的是（     ）A、c=a·sinA　  B、b=c·cosA    C、b=a·tanA    D、a=c·cosA  2．在Rt△ABC中，∠C=90°，AC=9．sin∠B=,则AB=（    ）A．15            B．12                C．9                D．63．已知∠A是锐角，sinA=，则5cosA=（ ）A．      B．        C．        D．5． 在△ABC中，∠B=45°, cosC=,   AC=5a, 则△ABC的 面积用a的式子表示是（   ）     A、10a2                 B、12 a2              C 、13a2          D、14a2二、填空题（每题5分，共25分）6．在Rt△ABC中∠C=90°，c=2，∠B=30°，则∠A=______，a=______，b=______.7．已知△ABC中，∠C=90°， 3 cosB=2, AC=2,  则AB=___________.8．已知一元二次方程3x2-13x＋4=0的解分别是Rt△ABC的一直角边长和∠A的正弦值，∠C=90°, 则AC= ____.9．如图，正方形ABCD的边长为4，点M在边DC上，M、N 两点关于对角线AC对称，若DM=1，则tan∠ADN=    ．10．（常州）在Rt△ABC中，∠C=90°，AC=2，BC=1，则tanB=       ，sinA=        。三、解答题（每题10分，共50分）11．在Rt△ABC中，∠C=90°，根据下列条件解直角三角形：（1）b=，c=4；            （2）b=7，∠A=45°；            （3）a=24，b=.      12．在Rt△ABC中，∠C=90°，sinA=，AB=15，求△ABC的周长和tanA的值    13．在Rt△ABC中，∠C=90°，∠A=60°，a+b=，解这个直角三角形.     14．（山东菏泽）如图，在△ABC中，∠C＝90º，∠A＝30º，BD是∠ABC的平分线，CD＝5cm，求AB的长．    15．（青岛）小明家所在居民楼的对面有一座大厦AB，AB＝米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：）解：         六、课后总结通过本节课的学习，你有什么收获？