

2022届天津南开中学高三第四次学情调查(数学)练习题
展开本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。第I卷1至3页,第II卷4至6页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。答卷时,考生务必将答案填涂在答题卡上,答在试卷上的无效。考试结束后,将答题卡交回。
祝各位考生考试顺利!
第I卷
注意事项:
每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。
本卷共9小题,每小题5分,共45分。
一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合U=1,2,3,4,5,6,7,A=1,3,5,7,B=1,2,3,4,则A⋂CUB=
(2)设x∈R,则“x>12”是“2x2+x-1>0”的
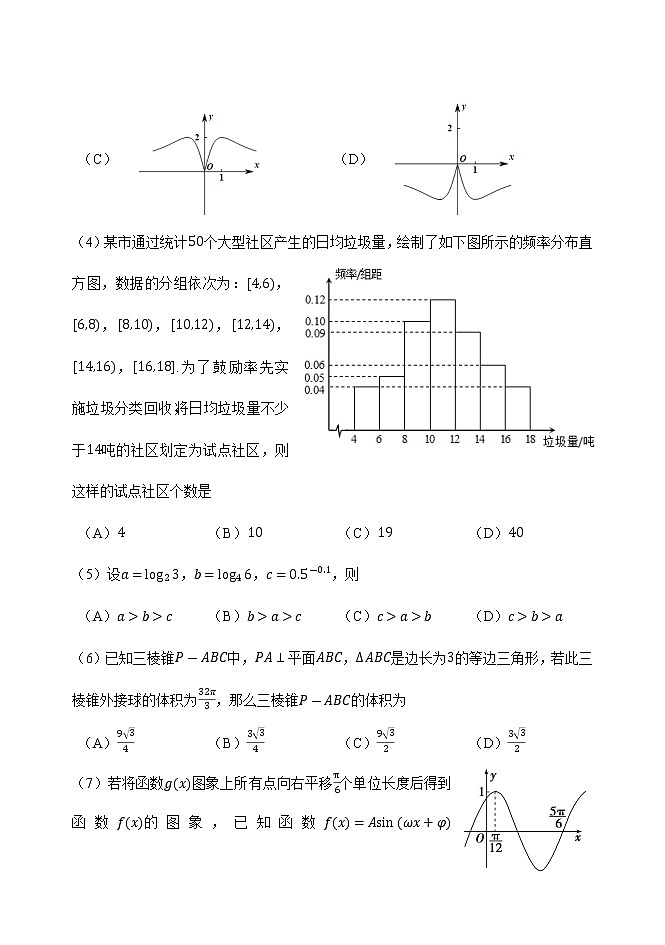
(3)函数y=-4xx2+1的图象大致为
(4)某市通过统计50个大型社区产生的日均垃圾量,绘制了如下图所示的频率分布直方图,数据的分组依次为:4,6,6,8,8,10,10,12,12,14,14,16,16,18.为了鼓励率先实施垃圾分类回收,将日均垃圾量不少于14吨的社区划定为试点社区,则这样的试点社区个数是
(5)设a=lg23,b=lg46,c=0.5-0.1,则
(6)已知三棱锥P-ABC中,PA⊥平面ABC,ΔABC是边长为3的等边三角形,若此三棱锥外接球的体积为32π3,那么三棱锥P-ABC的体积为
(7)若将函数gx图象上所有点向右平移π6个单位长度后得到函数fx的图象,已知函数fx=Asinωx+φA>0,ω>0,φ<π2的部分图象如图所示,则下列说法错误的是
(8)已知双曲线M:x2a2-y2b2=1a>0,b>0与抛物线N:y2=8x有一个公共的焦点F,若双曲线M与抛物线N的一个交点为P,且PF=5,则双曲线M的离心率为
(9)已知函数fx=2x2-8x+10,x>2,e2-x+x-1,x≤2,若fx≥x-m恒成立,则实数m的取值范围为
第II卷
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共11小题,共105分。
二.填空题:本大题共6小题,每小题5分,共30分.
(10)已知复数z=3+i1+i,则z= ____________.
(11)二项式x-x24的展开式中x3的系数为____________.
(12)过点M3,-1作一条直线l截圆x2+y2-2x+4y-4=0所得弦长为25,则直线l的方程是____________.
(13)已知正数a,b满足12a+1b=1ab,则4a2+ab+b2的最小值为____________.
(14)天津是一个古老与现代、保守与开放相融合的城市,历经600多年,特别是近代造就了中西合璧、古今兼容的独特城市风貌,成为国内外游客首选的旅游胜地. 2021年元月以来,来天津游览的游客络绎不绝,现通过对来津游客问卷调查,发现每位游客选择继续游玩的概率都是23,不游玩的概率都是13,若不游玩记1分,继续游玩记2分,游客之间选择意愿相互独立,从游客中随机抽取3人,记总得分为随机变量X,则X的数学期望EX=____________.
(15)如图,在菱形ABCD中,AB=3,∠BAD=60°,E,F分别为线段BC,CD上的点,CE=2EB,CF=2FD,点M在线段EF上,且满足AM=xAB+56ADx∈R,则x=____________;若点N为线段BD上一动点,则AN⋅MN的取值范围为____________.
三.解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.
(16)(本小题满分14分)
在ΔABC中,内角A,B,C的对边分别为a,b,c,已知2csC acsB+bcsA+c=0.
( = 1 \* ROMAN I)求角C的大小;
( = 2 \* ROMAN II)若a=2,b=2. 求:
(ⅰ)边长c;
(ⅱ)sin2B-C的值.
(17)(本小题满分15分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,BC∥AD,点M是棱PD上一点,且AB=BC=2,AD=PA=4.
( = 1 \* ROMAN I)若PM∶MD=1∶2,求证:PB∥平面ACM;
( = 2 \* ROMAN II)求二面角A-CD-P的正弦值;
( = 3 \* ROMAN III)若直线AM与平面PCD所成角的正弦值为63,求MD的长.
(18)(本小题满分15分)
设an是等差数列,bn是等比数列,公比大于0,其前n项和为Snn∈N*.已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6.
( = 1 \* ROMAN I)求an和bn的通项公式;
( = 2 \* ROMAN II)设数列-1an的前n项和为Tn.记cn=3+T2n-12b2n-1+3+T2n2b2n,求cn;
( = 3 \* ROMAN III)求.
(19)(本小题满分15分)
已知椭圆C∶x2a2+y2b2=1a>b>0过点2,22,点A为椭圆的右顶点,点B为椭圆的下顶点,且OA=2OB.
( = 1 \* ROMAN I)求椭圆C的方程;
( = 2 \* ROMAN II)过点A的直线l1与椭圆C交于另一点M,过点B的直线l2与椭圆交于另一点N,直线l1与l2的斜率的乘积为-14,点M和点N关于y轴对称,求直线l1的斜率.
(20)(本小题满分16分)
已知fx=sinnx,gx=lnx+mex.(n为正整数,m∈R)
( = 1 \* ROMAN I)若y=gx在x=1处的切线垂直于直线y=12x,求实数m的值;
( = 2 \* ROMAN II)当n=1时,设函数hx=x2-1-2fx,x∈0,π,证明:hx有且仅有1个零点;
( = 3 \* ROMAN III)当n=2时,证明:f'x2+gx
(C)5,7
(D)1,2,3,4,5,7
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
(A)
(B)
(C)
(D)
(A)4
(B)10
(C)19
(D)40
(A)a>b>c
(B)b>a>c
(C)c>a>b
(D)c>b>a
(A)934
(B)334
(C)932
(D)332
(A)fx在0,π4上的最小值是12
(B)4π3,0是fx的一个对称中心
(C)gx在π4,π2上单调递减
(D)gx的图象关于点π6,0对称
(A)5
(B)3
(C)233
(D)2
(A)18,5-2ln2
(B)-∞,4-2ln2
(C)14,4-2ln2
(D)14,5-2ln2
天津市南开中学2024届高三第四次月检测数学试卷及部分答案: 这是一份天津市南开中学2024届高三第四次月检测数学试卷及部分答案,共8页。
44,天津市第一中学滨海学校2024届高三第四次学业水平质量调查数学试卷(无答案): 这是一份44,天津市第一中学滨海学校2024届高三第四次学业水平质量调查数学试卷(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022届天津市南开中学高三上学期第四次学情调查数学试题含解析: 这是一份2022届天津市南开中学高三上学期第四次学情调查数学试题含解析,共18页。试卷主要包含了单选题,填空题,双空题,解答题等内容,欢迎下载使用。












