

2022年小升初数学模块专项复习培优练习题 模块25《图形与几何(培优)》(有答案,带解析)
展开2022年小升初数学模块专项复习培优练习题
模块25《图形与几何(培优)》
姓名:__________ 班级:__________考号:__________
题号
一
二
三
四
五
六
总分
评分
一、填空题
1.下图中,∠1=________,∠2=________。
2.有两根分别长5厘米和6厘米的小棒,再拿一根小棒来拼成一个三角形,第三根小棒的长度最长是________厘米,最短是________厘米。(取整厘米数)
3.一个等腰三角形中两个角的度数比是4:1,这个等腰三角形的顶角是________或________。
4.两个完全相同的直角三角形通过平移重叠在一起(如下图),涂色部分的面积是________平方分米。
5.如下图,长方形的面积与圆的面积相等,长方形的长是6厘米,圆的周长是________厘米。
6.3.2平方米=________平方分米 500平方米=________公顷
1.5立方米=________立方分米 0.3升=________毫升
7.一块石头放进鱼缸内后,水面的变化如下图,这块石头的体积是________立方厘米。
8.小青坐在教室的第3行、第4列,用(4,3)表示;小明坐在小青的左边,用数对________表示。
9.一个圆柱的体积是75.36立方米,与它等底等高的圆锥的体积是________立方米。
10.制作下面这个圆柱形薯片筒的侧面商标,需要________平方厘米的商标纸。
11.下图三角形三个顶点的位置用数对表示是A________、B________、C________。
二、判断题
12.从 的侧面看到的图形是轴对称图形。( )
13.圆周率是一个无限不循环的小数,保留两位小数约是3.14。( )
14.三角形中最大的角不小于60度。( )
15.圆锥的体积比与它等底等高的圆柱的体积小。( )
16.图形 中,大圆的周长与两个小圆的周长和相等。( )
三、选择题
17.用三角板不能画出的角是( )度。
A. 15 B. 105 C. 25 D. 135
18.下面( )中的两个图形只通过平移就可以重合。
A. B. C. D.
19.把4个棱长是1厘米的小正方体拼成1个长方体,这个长方体的表面积最少是( )平方厘米。
A. 16 B. 18 C. 22 D. 24
20.一个圆柱的侧面展开后是一个正方形,这个圆柱的底面半径和高的比是( )。
A. 1: π B. 1:2 π C. π:1 D. 2 π:1
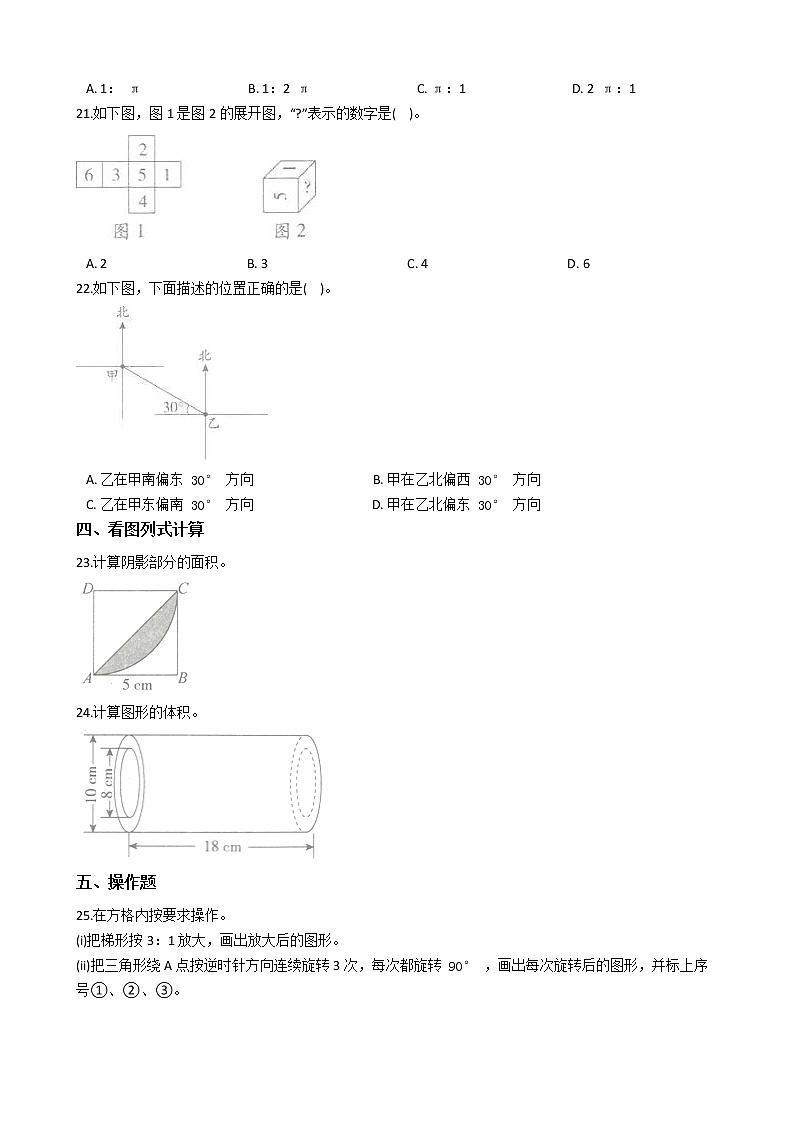
21.如下图,图1是图2的展开图,“?”表示的数字是( )。
A. 2 B. 3 C. 4 D. 6
22.如下图,下面描述的位置正确的是( )。
A. 乙在甲南偏东 30° 方向 B. 甲在乙北偏西 30° 方向
C. 乙在甲东偏南 30° 方向 D. 甲在乙北偏东 30° 方向
四、看图列式计算
23.计算阴影部分的面积。
24.计算图形的体积。
五、操作题
25.在方格内按要求操作。
(i)把梯形按3:1放大,画出放大后的图形。
(ii)把三角形绕A点按逆时针方向连续旋转3次,每次都旋转 90° ,画出每次旋转后的图形,并标上序号①、②、③。
26.李亮家附近的平面图如右图。
(1)从文化宫到超市怎么走?
(2)李亮家住在幸福小区,李亮步行平均每分钟走75米,他从家到公园半小时能走到吗?
六、解决问题
27.在一个长20厘米、宽16厘米的长方形的四个角上分别剪去一个边长2厘米的正方形,然后做成一个无盖的长方体容器。这个长方体容器的占地面积是多大?容积是多少立方厘米?
28.贝贝想测量一个瓶子的容积,瓶身呈圆柱形,如下图,她先将容积是1.2升的牛奶瓶中装满水,然后将水注入此瓶中,当瓶正放时瓶内水高15厘米,当瓶倒放时空着的部分高2.5厘米。你能根据这些信息求出瓶子的容积吗?
29.营养学家建议:儿童每日喝水应不少于1500毫升。青青每天用底面直径是6厘米,高是10厘米的水杯喝6满杯水,达到要求了吗?
30.下图是一块长方形铁皮,阴影部分刚好能做成一个圆柱形油桶(接头处不计)。求这个油桶的容积。(单位:分米)
31.一种儿童玩具—陀螺(如下图),上面是圆柱,下面是圆锥。圆柱的直径是6厘米,高是8厘米,圆锥的高是圆柱的高的 34 ,这个陀螺的体积是多少立方厘米?(保留整立方厘米)
答案解析部分
一、填空题
1.【答案】 60°;150°
【考点】角的度量(计算)
【解析】【解答】图中,根据平角的定义用180°减去30°角即可求得∠2的度数,再根据直角的定义用90°减去30°角即可求得∠1的度数。
【分析】考查了角的度量,关键是熟悉平角的度数是180°以及直角的度数是90°的知识点。
2.【答案】 10;2
【考点】三角形的特点
【解析】【解答】6-5<第三边<6+5, 所以,1<第三边<11, 答:再找一根最长是10厘米、最短是2厘米小棒就可以围成一个三角形。
故答案为:10,2。
【分析】根据三角形的两边之和大于第三边,两边之差小于第三边分析解答即可。
3.【答案】 20°;120°
【考点】等腰三角形认识及特征,三角形的内角和,比的应用
【解析】【解答】(1)当顶角与底角的比是1:4时,顶角占三角形内角和的11+4+4 , 180°×11+4+4=180°×19=20°。
(2)当顶角与底角的比是4:1时,顶角占三角形内角和的44+1+1 , 180°×44+1+1=120°。
故答案为:20° , 120°。
【分析】根据三角形的内角和是180度,可分情况讨论:(1)顶角与底角的比是4:1,(2)顶角与底角的比是1:4.据此解答。
4.【答案】 57
【考点】重叠问题
【解析】【解答】(11-3)+11]×6÷2=(8+11)×6÷2=19×6÷2=57(平方厘米)。
答:阴影部分的面积是57平方厘米。
故答案为:57平方厘米。
【分析】由图意可知:阴影部分的面积就等于梯形的面积,梯形的下底和高已知,上底可以求出,从而利用梯形面积公式即可求解。
5.【答案】 12
【考点】图形的拼组
【解析】【解答】设圆的半径为r:πr2=6r,求得r=1.91厘米;
圆的周长:3.14×2r=12厘米。
【分析】答本题的关键是求出圆的半径,因为求出圆的半径后,即可求出圆的面积(长方形的面积)进而求出长方形的周长。
6.【答案】 320
;0.05
;1500
;300
【考点】含小数的单位换算,平方厘米、平方分米、平方米之间的换算与比较,公顷、平方千米与平方米之间的换算与比较,体积单位间的进率及换算,容积单位间的进率及换算
【解析】【解答】3.2平方米=320平方分米; 500平方米=0.05公顷; 1.5立方米=1500立方分米 ;0.3升=300毫升。
故答案为:320,0.05,1500,300。
【分析】 把3.2平方米化成平方分米数,用3.2乘进率100; 把500平方米化成公顷数,用500除以进率10000; 把1.5立方米化成立方分米数,用1.5乘进率1000; 把0.3升化成毫升数,用0.3乘进率1000;即可得解.。
7.【答案】 64
【考点】长方形、正方形的面积
【解析】【解答】8×8×1=64(立方厘米)。
答:这块石头的体积是64立方厘米。
故答案为:64。
【分析】已知正方体玻璃鱼缸的底面边长,可得底面积,水上升的体积就是石头的体积,底面积乘上升的高度即可得石头的体积。
8.【答案】 (5,3)
【考点】数对与位置
【解析】【解答】小青坐在教室的第3行第4列,小明坐在小青的左边,所以小明与小青都坐在第3行,小青在第4列,则小明在第5列,所以小明的位置是:(5,3)。
故答案为:(5,3)。
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解答。
9.【答案】 25.12
【考点】圆锥的体积(容积)
【解析】【解答】75.36×13=25.12(立方米)。
答:圆锥的体积是25.12立方米。
故答案为:25.12。
【分析】等底等高的圆锥的体积是圆柱体积13 , 已知圆柱的体积,求圆锥的体积,根据一个数乘分数的意义,用乘法解答。
10.【答案】 188.4
【考点】圆柱的侧面积、表面积
【解析】【解答】3.14×(3×2)×10=3.14×6×10=18.84×10=188.4(平方厘米)。
答:需要188.4平方厘米的纸。
【分析】本题考点:关于圆柱的应用题。
此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际进行解答。
要求制作这个薯片筒的侧面标签所需要纸的面积就是求底面半径为3厘米,高为10厘米的圆柱体的侧面积,由此利用圆柱的侧面积=底面周长×高即可计算。
11.【答案】 (3,1)
;(6,4)
;(4,4)
【考点】平移与平移现象,数对与位置
【解析】【解答】根据数对表示位置的方法可得:A的位置是(3,1);B的位置是(6,4);C的位置是(4,4);
故答案为:(1)A(3,1);B(6,4);C(4,4)。
【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行.由此即可标出图中三角形三个顶点的位置。
二、判断题
12.【答案】 错误
【考点】轴对称,从不同方向观察几何体
【解析】【解答】从左侧看为:, 从右侧看为:, 都不是轴对称图形。
故答案为:错误。
【分析】此题考查了从不同的方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
13.【答案】 正确
【考点】圆、圆心、半径与直径的认识
【解析】【解答】由分析可知:圆周率是一个无限不循环小数;
故答案为:正确。
【分析】根据圆周率的含义:圆的周长和它直径的比值叫圆周率,它是一个无限不循环小数,用π表示,π=3.1415926…;进而得出结论。
14.【答案】 正确
【考点】三角形的内角和
【解析】【解答】假设三角形的最大内角小于60°,那么三角形的内角和就小于180°,与三角形内角和为180°相矛盾。
因此三角形中最大的内角不能小于60°;
故答案为:正确。
【分析】根据三角形的内角和等于180°,然后运用假设法,即可得出结论。
15.【答案】 正确
【考点】圆柱的侧面积、表面积,圆锥的体积(容积)
【解析】【解答】因为等底等高的圆锥的体积是圆柱的体积的13 , 所以圆锥的体积比与它等底等高的圆柱的体积小。
故答案为:正确。
【分析】因为圆柱和圆锥在“等底等高”的条件下,圆锥的体积是圆柱体积的13 , 据此即可判断。
16.【答案】 正确
【考点】组合图形的周长的巧算
【解析】【解答】大圆的周长与两个小圆的周长和相等,正确;
故答案为:正确。
【分析】因为两个小圆的直径和等于大圆的直径,周长=πd,所以图中的大圆内的两个小圆的周长之和等于大圆的周长,由此即可进行判断。
三、选择题
17.【答案】 C
【考点】根据度数画角
【解析】【解答】A、15°的角,45°-30°=15°,能画出的角; B、105°的角,45°+60°=105°,能画出的角; C、25°的角,无法用三角板中角的度数拼出; D、135°的角,45°+90°=135°,能画出的角。
故选:C。
【分析】用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数。
18.【答案】 D
【考点】作平移后的图形
【解析】【解答】A.对应点的连线平行,平移后不能重合,不符合题意;B.对应点的连线相交,平移后不能重合,不符合题意; C.对应点的连线相交,平移后不能重合,不符合题意;D. 对应点的连线平行,平移后能重合,符合题意。
故答案为:D。
【分析】找到平移前后形状与大小没有改变,并且对应点的连线平行且相等的图形即可。
19.【答案】 A
【考点】长方体和正方体的表面积
【解析】【解答】原来的面数是4×6=24面,
①拼成长宽高分别为4厘米、1厘米、1厘米的长方体,减少的面数是6,(24-6)×1×1=18(平方厘米);
②拼成长宽高分别为2厘米、2厘米、1厘米的长方体,减少的面数是8,(24-8)×1×1=16(平方厘米);
因为18>16。所以表面积最少是16平方厘米。
故答案为:A.
【分析】有两种拼法:①拼成长宽高分别为4厘米、1厘米、1厘米的长方体,减少的面数是6;②拼成长宽高分别为2厘米、2厘米、1厘米的长方体,减少的面数是8,根据正方形的面积公式:S=a2 , 即可解决问题。
20.【答案】 B
【考点】圆柱的展开图,圆柱的侧面积、表面积
【解析】【解答】设底面半径为r,那么底面周长为2πr,
因为圆柱的底面周长=圆柱的高,
所以圆柱的底面半径:圆柱的高=底面半径:底面周长=r:2πr=1:2π。
故答案为:B。
【分析】根据题意,这个圆柱体的底面周长等于高,底面半径和高的比就是底面半径和底面周长的比,设圆柱体的底面半径为r,那么底面周长为2πr,最后用底面半径r和底面周长2πr进行比,进行化简后即可得到答案。
21.【答案】 C
【考点】正方体的展开图
【解析】【解答】如图:
根据正方体展开图的特征,图1折叠成正方体时,与5号面与1号面相邻的是2号面和4号面,当我们面对5号面,且1号面在上面时,右面是4号面. 故选:C.
【分析】如图,根据正方体展开图的11种特征,属于“1-4-1”型,折叠成正方体后,1号面与3号面相对,2号面与4号百相对,5号面与6号面相对,与5号面与1号面相邻的是2号面和4号面,当我们面对5号面,且1号面在上面时,右面是4号面.
22.【答案】 C
【考点】根据方向和距离确定物体的位置
【解析】【解答】乙在甲东偏南 30 ° 方向。
【分析】甲在乙的北偏西60°的方向上,是以乙为观察点,根据方向的相对性,以甲为观察点,甲的方向与乙的方向相反,角度相等,据此解答。
四、看图列式计算
23.【答案】 解:
3.14×52× 14 -5×5÷2=7.125(平方厘米)
【考点】组合图形面积的巧算
【解析】【分析】阴影部分的面积= 14圆的面积-三角形的面积;运用三角形、圆的面积公式解答即可。
24.【答案】 解:
10÷2=5(厘米)
8÷2=4(厘米)
3.14×(52-42)×18=508.68(立方厘米)
【考点】组合体的体积的巧算
【解析】【分析】由图意可知:这个图形的体积=圆环的面积×这个图形的高度,将数据代入此关系式即可求解。
五、操作题
25.【答案】 解:(i)梯形按3:1放大后的图形如图红色部分;
(ii) 三角形绕A点按逆时针方向连续旋转3次的图形如图①、②、③
【考点】图形的缩放,数对与位置
【解析】【分析】此题主要考查了数对表示位置的方法的应及旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
(1)按3:1的比例画出梯形放大后的图形,就是把原梯形的上底、下底和高分别扩大到原来的3倍,原梯形的上底、下底和高分别是2格、3格和1格,扩大后的梯形的上底、下底和高分别是6格、9格和3格。
(2)根据旋转图形的特征,三角形ABC绕点A旋转90°后,点A的位置不动,其余各部分均绕点A按相同的方向,旋转相同的度数,即可三角形ABC绕点A按逆时针方向旋转90°后得到的图形①、②、③。
26.【答案】 (1)解:先向东走450米,再向东北方向走600米,再向东走680米。
(2)解:680+720+700=2100(米)
75×30=2250(米)
2100<2250
所以他从家到公园半小时能走到。
【考点】根据方向和距离确定物体的位置
【解析】【分析】此题主要考查依据方向(角度)和距离判定物体位置的方法。
(1)根据上北下南左西右东,从文化宫到超市,要先向东走450米,再向东北方向走600米,再向东走680米。
(2)李亮家从幸福小区步行到公园,要先向东走680米,再向北走720米,最后向南偏东36o走700米,即可算得总路程。
六、解决问题
27.【答案】 20-2-2=16(厘米)
16-2-2=12(厘米)
16×12=192(平方厘米)
192×2=384(立方厘米)
答:这个长方体容器的占地面积是192平方厘米,容积是384立方厘米。
【考点】长方体和正方体的表面积
【解析】【分析】首先根据题意,用长方形硬纸板的长减去正方形的边长的2倍,求出长方体纸盒的长是多少;然后用长方形硬纸板的宽减去正方形的边长的2倍,求出长方体纸盒的宽是多少;
所以占地面积=长乘以宽,最后根据长方体的容积=长×宽×高,求出这个纸盒的容积是多少立方厘米即可。
28.【答案】 1.2升=1.2立方分米=1200立方厘米
1200÷15=80(平方厘米)
80×2.5=200(立方厘米)
200立方厘米=0.2立方分米=0.2升
1.2+0.2=1.4(升)
答:瓶子的容积是1.4(升)
【考点】等积变形(位移、割补)
【解析】【分析】瓶内水的体积和高度已知,则可以求出瓶的底面积,而倒放时空余部分的高度已知,利用圆柱的体积的计算方法,即可求出空余部分的体积,所以瓶子的体积=饮料的体积+倒放时空余部分的体积。
29.【答案】 解: 3.14×(62)2×10×6 =1695.6(立方厘米)
1695.6立方厘米=1695.6毫升
1500<1695.6
所以达到要求了。
【考点】圆柱的体积(容积)
【解析】【分析】根据圆柱的体积公式,求出青青喝水的水杯的容积,再求出青青每天一共喝水的毫升数,最后与1500毫升进行比较,即可得出判断。
30.【答案】 设圆的直径为d分米,则d+πd=16.56, 4.14d=16.56, d=4;
油桶的体积:3.14×(42)2×(4×2)=3.14×4×8=12.56×8=100.48(立方分米),
答:这个桶的容积是100.48立方分米.
【考点】圆柱的展开图,圆柱的体积(容积)
【解析】【分析】由图意可知:长方形的宽等于圆的直径的2倍,油桶的高等于长方形的宽,且圆的直径+底面周长=长方形的长,长方形的长已知,从而可以分别求出油桶的底面积和高,进而求出油桶的体积。
31.【答案】 解: 3.14×(6÷2)2×8+3.14×(6÷2)2×(8×34)×13= 282.6≈283(立方厘米)
所以这个陀螺的体积是283立方厘米。
【考点】组合体的体积的巧算
【解析】【分析】由图意可知:陀螺的体积是圆柱与圆锥的体积之和,由“圆柱直径6厘米,高8厘米,圆锥的高是圆柱高的 34 ”即可先求出圆柱和圆锥的底面积,进而能分别求出二者的体积,将它们的体积加在一起,就是陀螺的体积。
2022年小升初数学模块专项复习培优练习题 模块24《图形与几何(基础)》(有答案,带解析): 这是一份2022年小升初数学模块专项复习培优练习题 模块24《图形与几何(基础)》(有答案,带解析),共16页。试卷主要包含了填空题,判断题,选择题,看图列式计算,操作题,解决问题等内容,欢迎下载使用。
2022年小升初数学模块专项复习培优练习题 模块22《数与代数(培优)》(有答案,带解析): 这是一份2022年小升初数学模块专项复习培优练习题 模块22《数与代数(培优)》(有答案,带解析),共19页。试卷主要包含了填空题,判断题,选择题,计算题,解决问题等内容,欢迎下载使用。
2022年小升初数学模块专项复习培优练习题 模块19《统计》(有答案,带解析): 这是一份2022年小升初数学模块专项复习培优练习题 模块19《统计》(有答案,带解析),共26页。试卷主要包含了选择题,判断题,填空题,解答题等内容,欢迎下载使用。













