2022届江苏省徐州市树人初级中学中考二模数学试题含解析

这是一份2022届江苏省徐州市树人初级中学中考二模数学试题含解析，共21页。试卷主要包含了九年级，已知抛物线y＝ax2+bx+c等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．为了解中学300名男生的身高情况，随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图(如图)．估计该校男生的身高在169.5cm～174.5cm之间的人数有（ ）

A．12 B．48 C．72 D．96
2．若a与﹣3互为倒数，则a=（　　）
A．3 B．﹣3 C． D．-
3．如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（　　）

A．3a+2b B．3a+4b C．6a+2b D．6a+4b
4．2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（　　）
A． B．
C． D．
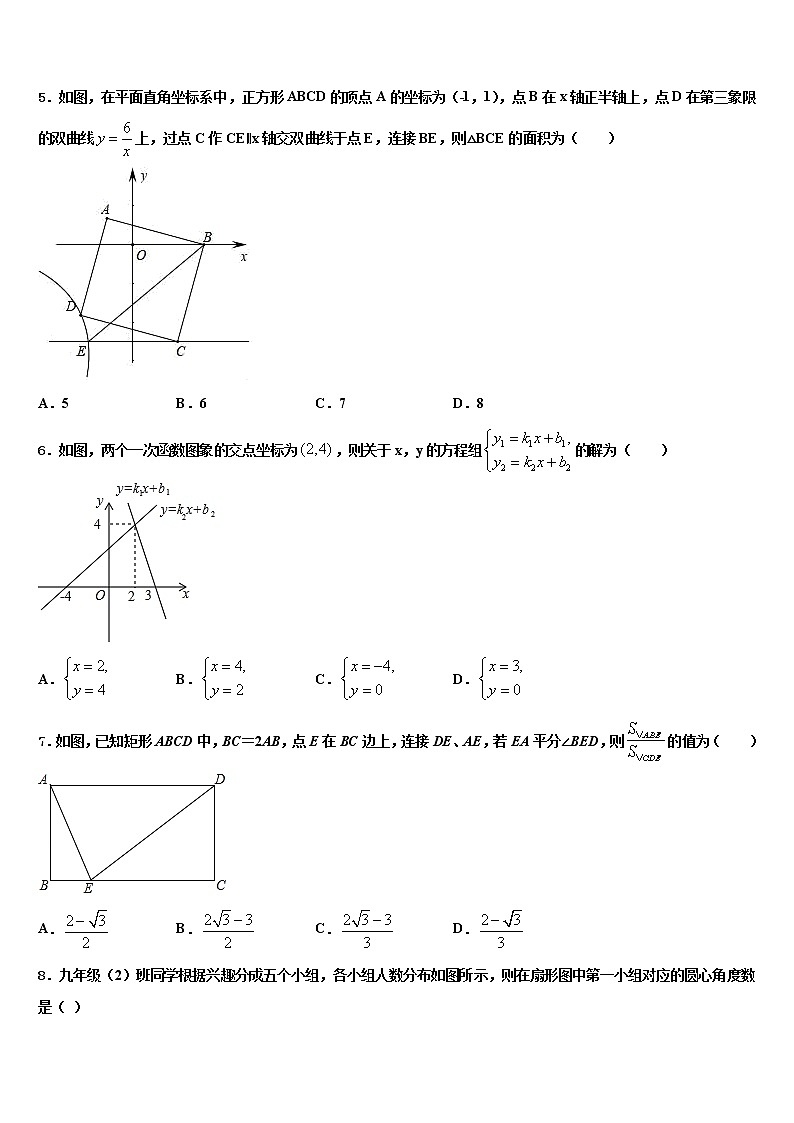
5．如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（﹣1，1），点B在x轴正半轴上，点D在第三象限的双曲线上，过点C作CE∥x轴交双曲线于点E，连接BE，则△BCE的面积为（　　）

A．5 B．6 C．7 D．8
6．如图，两个一次函数图象的交点坐标为，则关于x，y的方程组的解为（ ）

A． B． C． D．
7．如图，已知矩形ABCD中，BC＝2AB，点E在BC边上，连接DE、AE，若EA平分∠BED，则的值为（　　）

A． B． C． D．
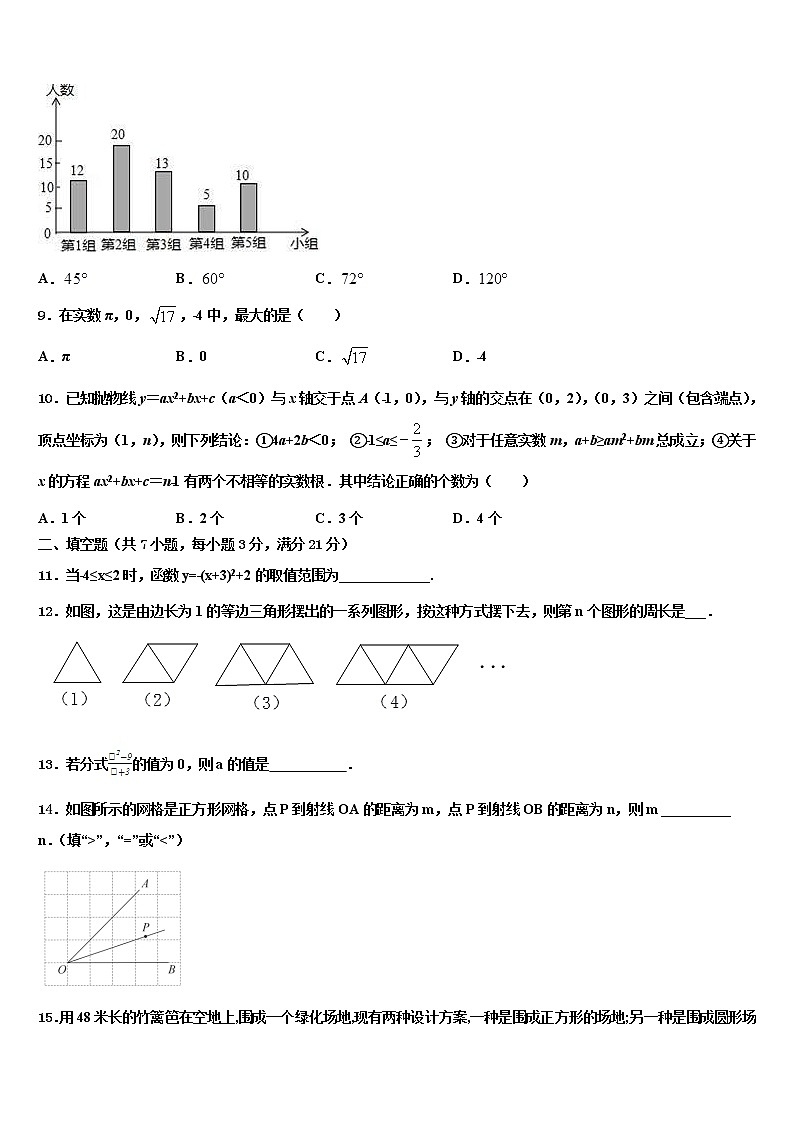
8．九年级（2）班同学根据兴趣分成五个小组，各小组人数分布如图所示，则在扇形图中第一小组对应的圆心角度数是（ ）

A． B． C． D．
9．在实数π，0，，﹣4中，最大的是（　　）
A．π B．0 C． D．﹣4
10．已知抛物线y＝ax2+bx+c（a＜0）与x轴交于点A（﹣1，0），与y轴的交点在（0，2），（0，3）之间（包含端点），顶点坐标为（1，n），则下列结论：①4a+2b＜0； ②﹣1≤a≤； ③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c＝n﹣1有两个不相等的实数根．其中结论正确的个数为（　　）
A．1个 B．2个 C．3个 D．4个
二、填空题（共7小题，每小题3分，满分21分）
11．当﹣4≤x≤2时，函数y=﹣(x+3)2+2的取值范围为_____________.
12．如图，这是由边长为1的等边三角形摆出的一系列图形，按这种方式摆下去，则第n个图形的周长是___．

13．若分式的值为0，则a的值是 ．
14．如图所示的网格是正方形网格，点P到射线OA的距离为m，点P到射线OB的距离为n，则m __________ n．（填“>”，“=”或“
【解析】
由图像可知在射线上有一个特殊点,点到射线的距离，点到射线的距离，于是可知 ,利用锐角三角函数 ,即可判断出
【详解】
由题意可知：找到特殊点，如图所示：

设点到射线的距离 ，点到射线的距离
由图可知，
,
,


【点睛】
本题考查了点到线的距离，熟知在直角三角形中利用三角函数来解角和边的关系是解题关键.
15、圆形
【解析】
根据竹篱笆的长度可知所围成的正方形的边长，进而可计算出所围成的正方形的面积；根据圆的周长公式，可知所围成的圆的半径，进而将圆的面积计算出来，两者进行比较．
【详解】
围成的圆形场地的面积较大．理由如下：
设正方形的边长为a，圆的半径为R，
∵竹篱笆的长度为48米，
∴4a=48，则a=1．即所围成的正方形的边长为1；2π×R=48，
∴R=，即所围成的圆的半径为，
∴正方形的面积S1=a2=144，圆的面积S2=π×（）2=，
∵144＜，
∴围成的圆形场地的面积较大．
故答案为：圆形．
【点睛】
此题主要考查实数的大小的比较在实际生活中的应用，所以学生在学这一部分时一定要联系实际，不能死学．
16、．
【解析】
用被抽查的100名学生中参加社会实践活动时间在2～2.5小时之间的学生除以抽查的学生总人数，即可得解．
【详解】
由频数分布直方图知，2～2.5小时的人数为100﹣（8+24+30+10）=28，则该校双休日参加社会实践活动时间在2～2.5小时之间的学生数大约是全体学生数的百分比为100%=28%．
故答案为：28%．
【点睛】
本题考查了频数分布直方图以及用样本估计总体，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．
17、8π
【解析】
圆锥的侧面积就等于母线长乘底面周长的一半．依此公式计算即可．
【详解】
侧面积=4×4π÷2=8π．
故答案为8π．
【点睛】
本题主要考查了圆锥的计算，正确理解圆锥的侧面积的计算可以转化为扇形的面积的计算，理解圆锥与展开图之间的关系．

三、解答题（共7小题，满分69分）
18、（1）5+；（2）
【解析】
试题分析：（1）先分别进行绝对值化简，0指数幂、负指数幂的计算，特殊三角函数值、二次根式的化简，然后再按运算顺序进行计算即可；
（2）括号内先通分进行加法运算，然后再进行分式除法运算，最后代入数值进行计算即可.
试题解析：（1）原式=2﹣1+4﹣2×+2=2﹣1+4﹣+2=5+；
（2）原式==，
当a=时，原式==．
19、 (1)见解析；（2）m=2
【解析】
（1）根据一元二次方程根的判别式进行分析解答即可；
（2）用“因式分解法”解原方程，求得其两根，再结合已知条件分析解答即可.
【详解】
（1）∵在方程x2﹣6mx+9m2﹣9=1中，△=（﹣6m）2﹣4（9m2﹣9）=26m2﹣26m2+26=26＞1．
∴方程有两个不相等的实数根；
（2）关于x的方程：x2﹣6mx+9m2﹣9=1可化为：[x﹣（2m+2）][x﹣（2m﹣2）]=1，
解得：x=2m+2和x=2m-2，
∵2m+2＞2m﹣2，x1＞x2，
∴x1=2m+2，x2=2m﹣2，
又∵x1=2x2，
∴2m+2=2（2m﹣2）解得：m=2．
【点睛】
（1）熟知“一元二次方程根的判别式：在一元二次方程中，当时，原方程有两个不相等的实数根，当时，原方程有两个相等的实数根，当时，原方程没有实数根”是解答第1小题的关键；（2）能用“因式分解法”求得关于x的方程x2﹣6mx+9m2﹣9=1的两个根是解答第2小题的关键.
20、R= 或R=
【解析】
解：当圆与斜边相切时，则R=，即圆与斜边有且只有一个公共点，当R=时，点A在圆内，点B在圆外或圆上，则圆与斜边有且只有一个公共点．
考点：圆与直线的位置关系．
21、（1）C;(2)100
【解析】
（1）根据中位数的定义即可作出判断；
（2）先算出样本中C等级的百分比，再用总数乘以400即可.
【详解】
解：（1）由直方图中可知数据总数为40个，第20，21个数据的平均数为本组数据的中位数，第20，21个数据的等级都是C等级，故本次调查中，男生的跳绳成绩的中位数在C等级；
故答案为C.
（2）400 =100（人）
答：估计该校九年级男生跳绳成绩是等级的人数有100人.
【点睛】
本题考查了中位数的求法和用样本数估计总体数据，理解相关知识是解题的关键.
22、（1）图见解析；（2）126°；（3）1．
【解析】
（1）利用被调查学生的人数=了解程度达到B等的学生数÷所占比例，即可得出被调查学生的人数，由了解程度达到C等占到的比例可求出了解程度达到C等的学生数，再利用了解程度达到A等的学生数=被调查学生的人数-了解程度达到B等的学生数-了解程度达到C等的学生数-了解程度达到D等的学生数可求出了解程度达到A等的学生数，依此数据即可将条形统计图补充完整；
（2）根据A等对应的扇形圆心角的度数=了解程度达到A等的学生数÷被调查学生的人数×360°，即可求出结论；
（3）利用该校现有学生数×了解程度达到A等的学生所占比例，即可得出结论．
【详解】
（1）48÷40%=120（人），
120×15%=18（人），
120-48-18-12=42（人）．
将条形统计图补充完整，如图所示．

（2）42÷120×100%×360°=126°．
答：扇形统计图中的A等对应的扇形圆心角为126°．
（3）1500×=1（人）．
答：该校学生对政策内容了解程度达到A等的学生有1人．
【点睛】
本题考查了条形统计图、扇形统计图以及用样本估计总体，观察条形统计图及扇形统计图，找出各数据，再利用各数量间的关系列式计算是解题的关键．
23、（2）y=x2﹣4x+3；（2）①2＜x3＜4，②m的值为或2．
【解析】
（2）由直线y=﹣x+3分别与x轴、y交于点B、C求得点B、C的坐标，再代入y=x2+bx+c求得b、c的值，即可求得抛物线的解析式；（2）①先求得抛物线的顶点坐标为D（2，﹣2），当直线l2经过点D时求得m=﹣2；当直线l2经过点C时求得m=3，再由x2＞x2＞2，可得﹣2＜y3＜3，即可﹣2＜﹣x3+3＜3，所以2＜x3＜4；②分当直线l2在x轴的下方时，点Q在点P、N之间和当直线l2在x轴的上方时，点N在点P、Q之间两种情况求m的值即可.
【详解】
（2）在y=﹣x+3中，令x=2，则y=3；
令y=2，则x=3；得B（3，2），C（2，3），
将点B（3，2），C（2，3）的坐标代入y=x2+bx+c
得：，解得
∴y=x2﹣4x+3；
（2）∵直线l2平行于x轴，
∴y2=y2=y3=m，
①如图①，y=x2﹣4x+3=（x﹣2）2﹣2，
∴顶点为D（2，﹣2），
当直线l2经过点D时，m=﹣2；
当直线l2经过点C时，m=3
∵x2＞x2＞2，
∴﹣2＜y3＜3，
即﹣2＜﹣x3+3＜3，
得2＜x3＜4，
②如图①，当直线l2在x轴的下方时，点Q在点P、N之间，
若三个点P、Q、N中恰好有一点是其他两点所连线段的中点，则得PQ=QN．
∵x2＞x2＞2，
∴x3﹣x2=x2﹣x2，
即 x3=2x2﹣x2，
∵l2∥x轴，即PQ∥x轴，
∴点P、Q关于抛物线的对称轴l2对称，
又抛物线的对称轴l2为x=2，
∴2﹣x2=x2﹣2，
即x2=4﹣x2，
∴x3=3x2﹣4，
将点Q（x2，y2）的坐标代入y=x2﹣4x+3
得y2=x22﹣4x2+3，又y2=y3=﹣x3+3
∴x22﹣4x2+3=﹣x3+3，
∴x22﹣4x2=﹣（3x2﹣4）
即 x22﹣x2﹣4=2，解得x2=，（负值已舍去），
∴m=（）2﹣4×+3=
如图②，当直线l2在x轴的上方时，点N在点P、Q之间，

若三个点P、Q、N中恰好有一点是其他两点所连线段的中点，则得PN=NQ．
由上可得点P、Q关于直线l2对称，
∴点N在抛物线的对称轴l2：x=2，
又点N在直线y=﹣x+3上，
∴y3=﹣2+3=2，即m=2．
故m的值为或2．
【点睛】
本题是二次函数综合题，
本题为二次函数的综合应用，涉及待定系数法、函数图象的交点、线段的中点及分类讨论思想等知识．在（2）中注意待定系数法的应用；在（2）①注意利用数形结合思想；在（2）②注意分情况讨论．本题考查知识点较多，综合性较强，难度较大．
24、见解析
【解析】
试题分析：探究：由四边形ABCD、四边形CEFG均为菱形，利用SAS易证得△BCE≌△DCG，则可得BE=DG；
应用：由AD∥BC，BE=DG，可得S△ABE+S△CDE=S△BEC=S△CDG=8，又由AE=3ED，可求得△CDE的面积，继而求得答案．
试题解析：
探究：∵四边形ABCD、四边形CEFG均为菱形，
∴BC=CD，CE=CG，∠BCD=∠A，∠ECG=∠F．
∵∠A=∠F，
∴∠BCD=∠ECG．
∴∠BCD-∠ECD=∠ECG-∠ECD，
即∠BCE=∠DCG．
在△BCE和△DCG中，

∴△BCE≌△DCG（SAS），
∴BE=DG．
应用：∵四边形ABCD为菱形，
∴AD∥BC，
∵BE=DG，
∴S△ABE+S△CDE=S△BEC=S△CDG=8，
∵AE=3ED，
∴S△CDE= ,
∴S△ECG=S△CDE+S△CDG=10
∴S菱形CEFG=2S△ECG=20.