

2022年福建省沙县中考数学押题卷含解析
展开2021-2022中考数学模拟试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.某公园里鲜花的摆放如图所示,第①个图形中有3盆鲜花,第②个图形中有6盆鲜花,第③个图形中有11盆鲜花,……,按此规律,则第⑦个图形中的鲜花盆数为()
A.37 B.38 C.50 D.51
2.4的平方根是( )
A.2 B.±2 C.8 D.±8
3.北京故宫的占地面积达到720 000平方米,这个数据用科学记数法表示为( )
A.0.72×106平方米 B.7.2×106平方米
C.72×104平方米 D.7.2×105平方米
4.下列各式中正确的是( )
A. =±3 B. =﹣3 C. =3 D.
5.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
6.实数a,b,c,d在数轴上的对应点的位置如图所示,下列结论①a<b;②|b|=|d|;③a+c=a;④ad>0中,正确的有( )
A.4个 B.3个 C.2个 D.1个
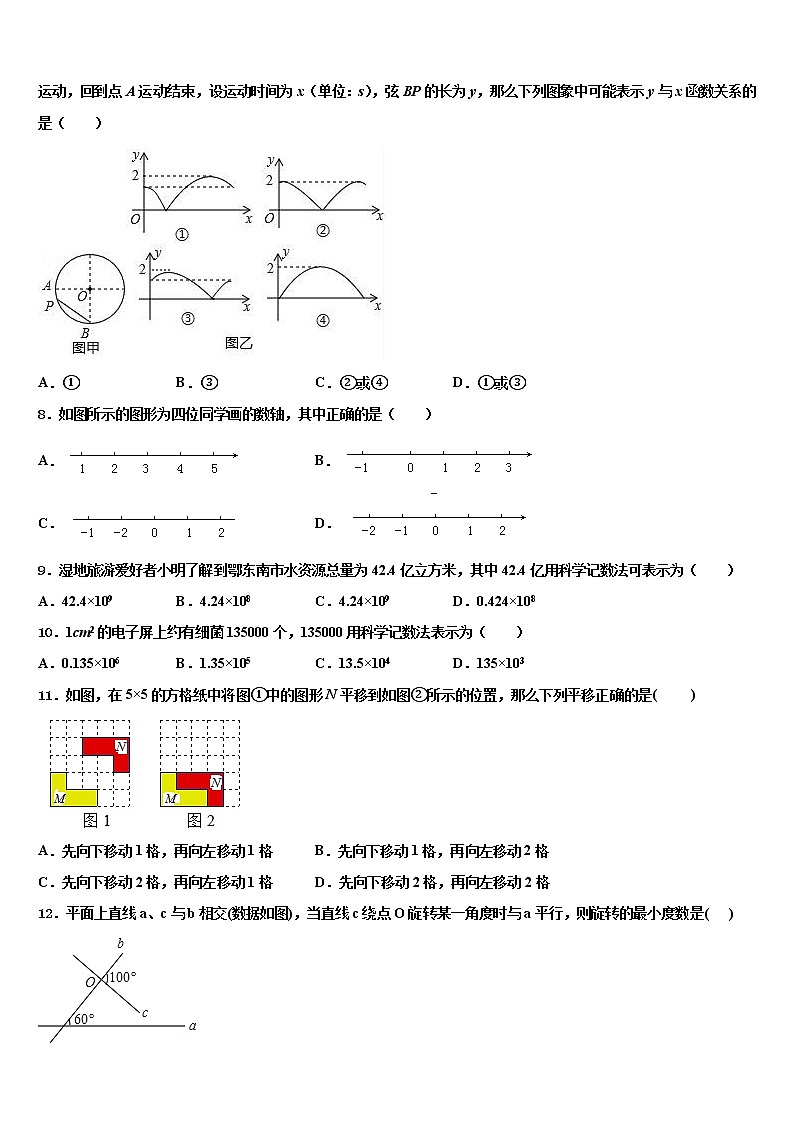
7.如图,A,B是半径为1的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到点A运动结束,设运动时间为x(单位:s),弦BP的长为y,那么下列图象中可能表示y与x函数关系的是( )
A.① B.③ C.②或④ D.①或③
8.如图所示的图形为四位同学画的数轴,其中正确的是( )
A. B.
C. D.
9.湿地旅游爱好者小明了解到鄂东南市水资源总量为42.4亿立方米,其中42.4亿用科学记数法可表示为( )
A.42.4×109 B.4.24×108 C.4.24×109 D.0.424×108
10.1cm2的电子屏上约有细菌135000个,135000用科学记数法表示为( )
A.0.135×106 B.1.35×105 C.13.5×104 D.135×103
11.如图,在5×5的方格纸中将图①中的图形N平移到如图②所示的位置,那么下列平移正确的是( )
A.先向下移动1格,再向左移动1格 B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格 D.先向下移动2格,再向左移动2格
12.平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
A.60° B.50° C.40° D.30°
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13.如图,利用标杆测量建筑物的高度,已知标杆高1.2,测得,则建筑物的高是__________.
14.若a,b互为相反数,则a2﹣b2=_____.
15.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示,按照这样的规律,摆第n个图,需用火柴棒的根数为_______________.
16.如图,边长为4的正方形ABCD内接于⊙O,点E是弧AB上的一动点(不与点A、B重合),点F是弧BC上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
①弧AE=弧BF;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+2.
其中正确的是_____.(把你认为正确结论的序号都填上)
17.如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么k的值是_______
18.一组数据4,3,5,x,4,5的众数和中位数都是4,则x=_____.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19.(6分)益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低.马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种
A
B
原来的运费
45
25
现在的运费
30
20
(1)求每次运输的农产品中A,B产品各有多少件;
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元.
20.(6分)为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:≈1.41,≈1.73,≈3.16)
21.(6分)八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
1
根据图表提供的信息,解答下列问题:八年级一班有多少名学生?请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.
22.(8分)为响应学校全面推进书香校园建设的号召,班长李青随机调查了若干同学一周课外阅读的时间(单位:小时),将获得的数据分成四组,绘制了如下统计图(:,:,:,:),根据图中信息,解答下列问题:
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示组的扇形统计图的圆心角的度数;
(3)如果李青想从组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或画树状图的方法求出选中甲的概率.
23.(8分)已知△ABC在平面直角坐标系中的位置如图所示.分别写出图中点A和点C的坐标;画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;求点A旋转到点A′所经过的路线长(结果保留π).
24.(10分)解不等式组,并把解集在数轴上表示出来.
25.(10分)先化简,再求值:,其中.
26.(12分)某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
(1)本次调查的学生总数为_____人,被调查学生的课外阅读时间的中位数是_____小时,众数是_____小时;并补全条形统计图;
(2)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是_____;
(3)若全校九年级共有学生800人,估计九年级一周课外阅读时间为6小时的学生有多少人?
27.(12分)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
求证:△ABM∽△EFA;若AB=12,BM=5,求DE的长.
参考答案
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、D
【解析】
试题解析:
第①个图形中有 盆鲜花,
第②个图形中有盆鲜花,
第③个图形中有盆鲜花,
…
第n个图形中的鲜花盆数为
则第⑥个图形中的鲜花盆数为
故选C.
2、B
【解析】
依据平方根的定义求解即可.
【详解】
∵(±1)1=4,
∴4的平方根是±1.
故选B.
【点睛】
本题主要考查的是平方根的定义,掌握平方根的定义是解题的关键.
3、D
【解析】
试题分析:把一个数记成a×10n(1≤a<10,n整数位数少1)的形式,叫做科学记数法.
∴此题可记为1.2×105平方米.
考点:科学记数法
4、D
【解析】
原式利用平方根、立方根定义计算即可求出值.
【详解】
解:A、原式=3,不符合题意;
B、原式=|-3|=3,不符合题意;
C、原式不能化简,不符合题意;
D、原式=2-=,符合题意,
故选:D.
【点睛】
此题考查了立方根,以及算术平方根,熟练掌握各自的性质是解本题的关键.
5、D
【解析】
A、对重庆市初中学生每天阅读时间的调查,调查范围广适合抽样调查,故A错误;
B、对端午节期间市场上粽子质量情况的调查,调查具有破坏性,适合抽样调查,故B错误;
C、对某批次手机的防水功能的调查,调查具有破坏性,适合抽样调查,故C错误;
D、对某校九年级3班学生肺活量情况的调查,人数较少,适合普查,故D正确;
故选D.
6、B
【解析】
根据数轴上的点表示的数右边的总比左边的大,有理数的运算,绝对值的意义,可得答案.
【详解】
解:由数轴,得a=-3.5,b=-2,c=0,d=2,
①a<b,故①正确;②|b|=|d|,故②正确;③a+c=a,故③正确;④ad<0,故④错误;
故选B.
【点睛】
本题考查了实数与数轴,利用数轴上的点表示的数右边的总比左边的大,有理数的运算,绝对值的意义是解题关键.
7、D
【解析】
分两种情形讨论当点P顺时针旋转时,图象是③,当点P逆时针旋转时,图象是①,由此即可解决问题.
【详解】
分两种情况讨论:①当点P顺时针旋转时,BP的长从增加到2,再降到0,再增加到,图象③符合;
②当点P逆时针旋转时,BP的长从降到0,再增加到2,再降到,图象①符合.
故答案为①或③.
故选D.
【点睛】
本题考查了动点问题函数图象、圆的有关知识,解题的关键理解题意,学会用分类讨论的思想思考问题,属于中考常考题型.
8、D
【解析】
根据数轴三要素:原点、正方向、单位长度进行判断.
【详解】
A选项图中无原点,故错误;
B选项图中单位长度不统一,故错误;
C选项图中无正方向,故错误;
D选项图形包含数轴三要素,故正确;
故选D.
【点睛】
本题考查数轴的画法,熟记数轴三要素是解题的关键.
9、C
【解析】
科学记数法的表示形式为的形式,其中为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值>1时,是正数;当原数的绝对值<1时,是负数.
【详解】
42.4亿=4240000000,
用科学记数法表示为:4.24×1.
故选C.
【点睛】
考查科学记数法,掌握绝对值大于1的数的表示方法是解题的关键.
10、B
【解析】
根据科学记数法的表示形式(a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同;当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数).
【详解】
解:135000用科学记数法表示为:1.35×1.
故选B.
【点睛】
科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
11、C
【解析】
根据题意,结合图形,由平移的概念求解.
【详解】
由方格可知,在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是:先向下移动2格,再向左移动1格,故选C.
【点睛】
本题考查平移的基本概念及平移规律,是比较简单的几何图形变换.关键是要观察比较平移前后物体的位置.
12、C
【解析】
先根据平角的定义求出∠1的度数,再由平行线的性质即可得出结论.
【详解】
解:∵∠1=180°﹣100°=80°,a∥c,
∴∠α=180°﹣80°﹣60°=40°.
故选:C.
【点睛】
本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13、10.5
【解析】
先证△AEB∽△ABC,再利用相似的性质即可求出答案.
【详解】
解:由题可知,BE⊥AC,DC⊥AC
∵BE//DC,
∴△AEB∽△ADC,
∴,
即:,
∴CD=10.5(m).
故答案为10.5.
【点睛】
本题考查了相似的判定和性质.利用相似的性质列出含所求边的比例式是解题的关键.
14、1
【解析】
【分析】直接利用平方差公式分解因式进而结合相反数的定义分析得出答案.
【详解】∵a,b互为相反数,
∴a+b=1,
∴a2﹣b2=(a+b)(a﹣b)=1,
故答案为1.
【点睛】本题考查了公式法分解因式以及相反数的定义,正确分解因式是解题关键.
15、6n+1.
【解析】
寻找规律:不难发现,后一个图形比前一个图形多6根火柴棒,即:
第1个图形有8根火柴棒,
第1个图形有14=6×1+8根火柴棒,
第3个图形有10=6×1+8根火柴棒,
……,
第n个图形有6n+1根火柴棒.
16、①②④
【解析】
①根据ASA可证△BOE≌△COF,根据全等三角形的性质得到BE=CF,根据等弦对等弧得到 ,可以判断①;
②根据SAS可证△BOG≌△COH,根据全等三角形的性质得到∠GOH=90°,OG=OH,根据等腰直角三角形的判定得到△OGH是等腰直角三角形,可以判断②;
③通过证明△HOM≌△GON,可得四边形OGBH的面积始终等于正方形ONBM的面积,可以判断③;
④根据△BOG≌△COH可知BG=CH,则BG+BH=BC=4,设BG=x,则BH=4-x,根据勾股定理得到GH== ,可以求得其最小值,可以判断④.
【详解】
解:①如图所示,
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
,
∴△BOE≌△COF,
∴BE=CF,
∴ ,①正确;
②∵OC=OB,∠COH=∠BOG,∠OCH=∠OBG=45°,
∴△BOG≌△COH;
∴OG=OH,∵∠GOH=90°,
∴△OGH是等腰直角三角形,②正确.
③如图所示,
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH==,
∴其最小值为4+2,④正确.
故答案为:①②④
【点睛】
考查了圆的综合题,关键是熟练掌握全等三角形的判定和性质,等弦对等弧,等腰直角三角形的判定,勾股定理,面积的计算,综合性较强.
17、-12
【解析】
过E点作EF⊥OC于F,如图所示:
由条件可知:OE=OA=5,,
所以EF=3,OF=4,
则E点坐标为(-4,3)
设反比例函数的解析式是y=,
则有k=-4×3=-12.
故答案是:-12.
18、1
【解析】
一组数据中出现次数最多的数据叫做众数,由此可得出答案.
【详解】
∵一组数据1,3,5,x,1,5的众数和中位数都是1,
∴x=1,
故答案为1.
【点睛】
本题考查了众数的知识,解答本题的关键是掌握众数的定义.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19、(1)每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,(2)产品件数增加后,每次运费最少需要1120元.
【解析】
(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,根据表中的数量关系列出关于x和y的二元一次方程组,解之即可,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,根据(1)的结果结合图表列出W关于m的一次函数,再根据“总件数中B产品的件数不得超过A产品件数的2倍”,列出关于m的一元一次不等式,求出m的取值范围,再根据一次函数的增减性即可得到答案.
【详解】
解:(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,
根据题意得:
,
解得:,
答:每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,
增加供货量后A产品的数量为(10+m)件,B产品的数量为30+(8-m)=(38-m)件,
根据题意得:W=30(10+m)+20(38-m)=10m+1060,
由题意得:38-m≤2(10+m),
解得:m≥6,
即6≤m≤8,
∵一次函数W随m的增大而增大
∴当m=6时,W最小=1120,
答:产品件数增加后,每次运费最少需要1120元.
【点睛】
本题考查了一次函数的应用,二元一次方程组的应用和一元一次不等式得应用,解题的关键:(1)正确根据等量关系列出二元一次方程组,(2)根据数量关系列出一次函数和不等式,再利用一次函数的增减性求最值.
20、2.1.
【解析】
据题意得出tanB = , 即可得出tanA, 在Rt△ADE中, 根据勾股定理可求得DE, 即可得出∠FCE的正切值, 再在Rt△CEF中, 设EF=x,即可求出x, 从而得出CF=1x的长.
【详解】
解:
据题意得tanB=,
∵MN∥AD,
∴∠A=∠B,
∴tanA=,
∵DE⊥AD,
∴在Rt△ADE中,tanA=,
∵AD=9,
∴DE=1,
又∵DC=0.5,
∴CE=2.5,
∵CF⊥AB,
∴∠FCE+∠CEF=90°,
∵DE⊥AD,
∴∠A+∠CEF=90°,
∴∠A=∠FCE,
∴tan∠FCE=
在Rt△CEF中,CE2=EF2+CF2
设EF=x,CF=1x(x>0),CE=2.5,
代入得()2=x2+(1x)2
解得x=(如果前面没有“设x>0”,则此处应“x=±,舍负”),
∴CF=1x=≈2.1,
∴该停车库限高2.1米.
【点睛】
点评: 本题考查了解直角三角形的应用, 坡面坡角问题和勾股定理, 解题的关键是坡度等于坡角的正切值.
21、(1)41(2)15%(3)
【解析】
(1)用散文的频数除以其频率即可求得样本总数;
(2)根据其他类的频数和总人数求得其百分比即可;
(3)画树状图得出所有等可能的情况数,找出恰好是丙与乙的情况,即可确定出所求概率.
【详解】
(1)∵喜欢散文的有11人,频率为1.25,
∴m=11÷1.25=41;
(2)在扇形统计图中,“其他”类所占的百分比为 ×111%=15%,
故答案为15%;
(3)画树状图,如图所示:
所有等可能的情况有12种,其中恰好是丙与乙的情况有2种,
∴P(丙和乙)==.
22、(1)50人;(2)补全图形见解析,表示A组的扇形统计图的圆心角的度数为108°;(3).
【解析】
分析:(1)、根据B的人数和百分比得出样本容量;(2)、根据总人数求出C组的人数,根据A组的人数占总人数的百分比得出扇形的圆心角度数;(3)、根据题意列出树状图,从而得出概率.
详解:(1)被调查的总人数为19÷38%=50人;
(2)C组的人数为50﹣(15+19+4)=12(人),
补全图形如下:
表示A组的扇形统计图的圆心角的度数为360°×=108°;
(3)画树状图如下,
共有12个可能的结果,恰好选中甲的结果有6个, ∴P(恰好选中甲)=.
点睛:本题主要考查的是条形统计图和扇形统计图以及概率的计算法则,属于基础题型.理解频数、频率与样本容量之间的关系是解题的关键.
23、(1)、(2)见解析(3)
【解析】
试题分析:(1)根据点的平面直角坐标系中点的位置写出点的坐标;(2)根据旋转图形的性质画出旋转后的图形;(3)点A所经过的路程是以点C为圆心,AC长为半径的扇形的弧长.
试题解析:(1)A(0,4)C(3,1)
(2)如图所示:
(3)根据勾股定理可得:AC=3,则.
考点:图形的旋转、扇形的弧长计算公式.
24、﹣1≤x<1.
【解析】
求不等式组的解集首先要分别解出两个不等式的解集,然后利用口诀“同大取大,同小取小,大小小大中间找,大大小小找不到(”确定不等式组解集的公共部分.
【详解】
解不等式①,得x<1,
解不等式②,得x≥﹣1,
∴不等式组的解集是﹣1≤x<1.
不等式组的解集在数轴上表示如下:
25、,
【解析】
先根据完全平方公式进行约分化简,再代入求值即可.
【详解】
原式=-==,将a=+1代入得,原式===,故答案为.
【点睛】
本题主要考查了求代数式的值、分式的运算,解本题的要点在于正确化简,从而得到答案.
26、(1)50;4;5;画图见解析;(2)144°;(3)64
【解析】
(1)根据统计图可知,课外阅读达3小时的共10人,占总人数的20%,由此可得出总人数;求出课外阅读时间4小时与6小时男生的人数,再根据中位数与众数的定义即可得出结论;根据求出的人数补全条形统计图即可;
(2)求出课外阅读时间为5小时的人数,再求出其人数与总人数的比值即可得出扇形的圆心角度数;
(3)求出总人数与课外阅读时间为6小时的学生人数的百分比的积即可.
【详解】
解:(1)∵课外阅读达3小时的共10人,占总人数的20%,
∴=50(人).
∵课外阅读4小时的人数是32%,
∴50×32%=16(人),
∴男生人数=16﹣8=8(人);
∴课外阅读6小时的人数=50﹣6﹣4﹣8﹣8﹣8﹣12﹣3=1(人),
∴课外阅读3小时的是10人,4小时的是16人,5小时的是20人,6小时的是4人,
∴中位数是4小时,众数是5小时.
补全图形如图所示.
故答案为50,4,5;
(2)∵课外阅读5小时的人数是20人,
∴×360°=144°.
故答案为144°;
(3)∵课外阅读6小时的人数是4人,
∴800×=64(人).
答:九年级一周课外阅读时间为6小时的学生大约有64人.
【点睛】
本题考查了统计图与中位数、众数的知识点,解题的关键是熟练的掌握中位数与众数的定义与根据题意作图.
27、(1)见解析;(2)4.1
【解析】
试题分析:(1)由正方形的性质得出AB=AD,∠B=10°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=10°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=10°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)∵∠B=10°,AB=12,BM=5,
∴AM==13,AD=12,
∵F是AM的中点,
∴AF=AM=6.5,
∵△ABM∽△EFA,
∴,
即,
∴AE=16.1,
∴DE=AE-AD=4.1.
考点:1.相似三角形的判定与性质;2.正方形的性质.
2022年福建省沙县重点达标名校中考数学押题卷含解析: 这是一份2022年福建省沙县重点达标名校中考数学押题卷含解析,共21页。试卷主要包含了下列计算正确的是,二次函数的对称轴是,我省2013年的快递业务量为1,下列运算正确的是等内容,欢迎下载使用。
2022年福建省莆田市仙游县中考数学押题卷含解析: 这是一份2022年福建省莆田市仙游县中考数学押题卷含解析,共22页。试卷主要包含了比1小2的数是,若|a|=﹣a,则a为,已知二次函数y=a等内容,欢迎下载使用。
2022年福建省福州十八中学中考押题数学预测卷含解析: 这是一份2022年福建省福州十八中学中考押题数学预测卷含解析,共17页。试卷主要包含了运用图形变化的方法研究下列问题,下列二次根式中,最简二次根式是等内容,欢迎下载使用。












