2022年江苏省锡山高级中学毕业升学考试模拟卷数学卷含解析

这是一份2022年江苏省锡山高级中学毕业升学考试模拟卷数学卷含解析，共22页。试卷主要包含了考生必须保证答题卡的整洁，对于一组统计数据，如图等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
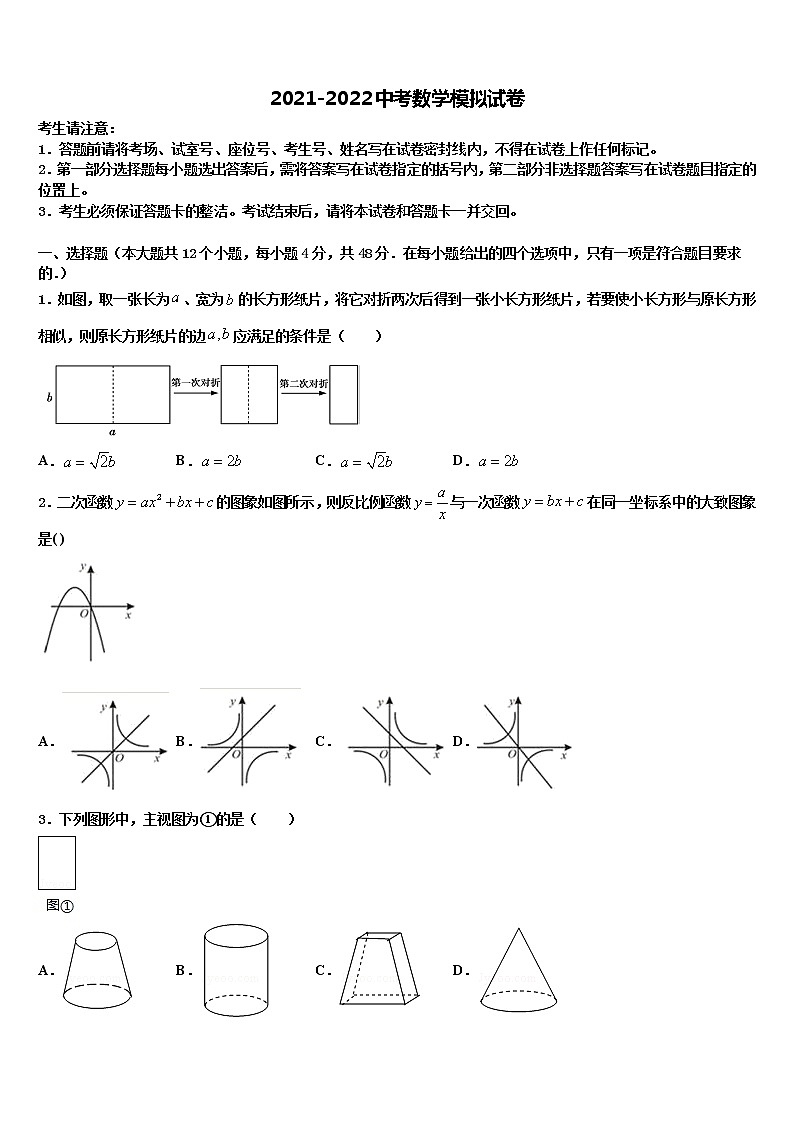
1．如图，取一张长为、宽为的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边应满足的条件是（ ）

A． B． C． D．
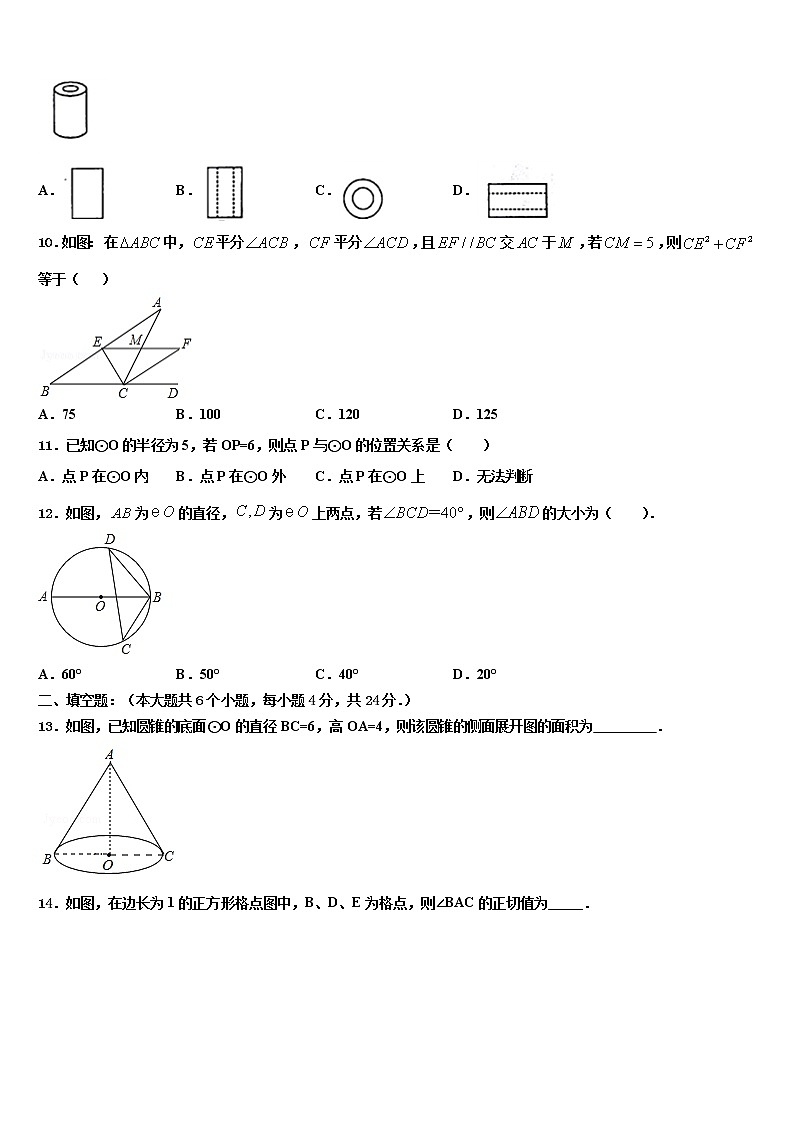
2．二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是( )

A． B． C． D．
3．下列图形中，主视图为①的是（　　）

A． B． C． D．
4．反比例函数y=的图象与直线y=﹣x+2有两个交点，且两交点横坐标的积为负数，则t的取值范围是（ ）
A．t＜ B．t＞ C．t≤ D．t≥
5．如图，Rt△ABC中，∠C=90°，∠A=35°，点D在边BC上，BD=2CD．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m=（　　）

A．35° B．60° C．70° D．70°或120°
6．对于一组统计数据：1，6，2，3，3，下列说法错误的是( )
A．平均数是3 B．中位数是3 C．众数是3 D．方差是2.5
7．如图是几何体的俯视图，所表示数字为该位置小正方体的个数，则该几何体的正视图是（ ）

A． B． C． D．
8．如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（　　）

A．90°-α B．90°+ α C． D．360°-α
9．图为一根圆柱形的空心钢管，它的主视图是( )

A． B． C． D．
10．如图： 在中，平分，平分，且交于，若，则等于（ ）

A．75 B．100 C．120 D．125
11．已知⊙O的半径为5，若OP=6，则点P与⊙O的位置关系是（　　）
A．点P在⊙O内 B．点P在⊙O外 C．点P在⊙O上 D．无法判断
12．如图，为的直径，为上两点，若，则的大小为（　　）．

A．60° B．50° C．40° D．20°
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如图，已知圆锥的底面⊙O的直径BC=6，高OA=4，则该圆锥的侧面展开图的面积为 ．

14．如图，在边长为1的正方形格点图中，B、D、E为格点，则∠BAC的正切值为_____．

15．在平面直角坐标系的第一象限内，边长为1的正方形ABCD的边均平行于坐标轴，A点的坐标为（a，a），如图，若曲线y＝（x＞0）与此正方形的边有交点，则a的取值范围是_______．

16．小明用一个半径为30cm且圆心角为240°的扇形纸片做成一个圆锥形纸帽（粘合部分忽略不计），那么这个圆锥形纸帽的底面半径为_____cm．
17．在数轴上与所对应的点相距4个单位长度的点表示的数是______．
18．如果一个正多边形每一个内角都等于144°，那么这个正多边形的边数是____．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）

20．（6分）如图，已知直线AB经过点（0，4），与抛物线y=x2交于A，B两点，其中点A的横坐标是．求这条直线的函数关系式及点B的坐标．在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在请说明理由．过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

21．（6分）在平面直角坐标系xOy中有不重合的两个点与.若Q、P为某个直角三角形的两个锐角顶点，当该直角三角形的两条直角边分别与x轴或y轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“直距”记做，特别地，当PQ与某条坐标轴平行（或重合）时，线段PQ的长即为点Q与点P之间的“直距”．例如下图中，点，点，此时点Q与点P之间的“直距”.
（1）①已知O为坐标原点，点，，则_________，_________；
②点C在直线上，求出的最小值；
（2）点E是以原点O为圆心，1为半径的圆上的一个动点，点F是直线上一动点.直接写出点E与点F之间“直距”的最小值．

22．（8分）如图，可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域，其中标有数字“1”的扇形圆心角为120°．转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次（若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）转动转盘一次，求转出的数字是－2的概率；转动转盘两次，用树状图或列表法求这两次分别转出的数字之积为正数的概率．

23．（8分）计算：﹣12+﹣（3.14﹣π）0﹣|1﹣|．
24．（10分）我市某学校在“行读石鼓阁”研学活动中，参观了我市中华石鼓园，石鼓阁是宝鸡城市新地标．建筑面积7200平方米，为我国西北第一高阁．秦汉高台门阙的建筑风格，追求稳定之中的飞扬灵动，深厚之中的巧妙组合，使景观功能和标志功能融为一体．小亮想知道石鼓阁的高是多少，他和同学李梅对石鼓阁进行测量．测量方案如下：如图，李梅在小亮和“石鼓阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，李梅看着镜面上的标记，她来回走动，走到点D时，看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合，这时，测得李梅眼睛与地面的高度ED=1.6米，CD=2.2米，然后，在阳光下，小亮从D点沿DM方向走了29.4米，此时“石鼓阁”影子与小亮的影子顶端恰好重合，测得小亮身高1.7米，影长FH=3.4米．已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“石鼓阁”的高AB的长度．

25．（10分）如图，点A、B在⊙O上，点O是⊙O的圆心，请你只用无刻度的直尺，分别画出图①和图②中∠A的余角.
（1）图①中，点C在⊙O上；
（2）图②中，点C在⊙O内；

26．（12分）如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．求证：△ADE≌△CBF；求证：四边形BFDE为矩形．

27．（12分）如图，在边长为1的小正方形组成的方格纸上，将△ABC绕着点A顺时针旋转90°
画出旋转之后的△AB′C′；求线段AC旋转过程中扫过的扇形的面积．



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，然后根据相似多边形的定义，列出比例式即可求出结论．
【详解】
解：由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，
∵小长方形与原长方形相似，


故选B．
【点睛】
此题考查的是相似三角形的性质，根据相似三角形的定义列比例式是解决此题的关键．
2、D
【解析】
根据抛物线和直线的关系分析.
【详解】
由抛物线图像可知，所以反比例函数应在二、四象限，一次函数过原点，应在二、四象限.
故选D
【点睛】
考核知识点：反比例函数图象.
3、B
【解析】
分析：主视图是从物体的正面看得到的图形，分别写出每个选项中的主视图，即可得到答案．
详解：A、主视图是等腰梯形，故此选项错误；
B、主视图是长方形，故此选项正确；
C、主视图是等腰梯形，故此选项错误；
D、主视图是三角形，故此选项错误；
故选B．
点睛：此题主要考查了简单几何体的主视图，关键是掌握主视图所看的位置．
4、B
【解析】
将一次函数解析式代入到反比例函数解析式中，整理得出x2﹣2x+1﹣6t=0，又因两函数图象有两个交点，且两交点横坐标的积为负数，根据根的判别式以及根与系数的关系可求解．
【详解】
由题意可得：﹣x+2=，
所以x2﹣2x+1﹣6t=0，
∵两函数图象有两个交点，且两交点横坐标的积为负数，
∴
解不等式组，得t＞．
故选：B．
点睛：此题主要考查了反比例函数与一次函数的交点问题，关键是利用两个函数的解析式构成方程，再利用一元二次方程的根与系数的关系求解.
5、D
【解析】
①当点B落在AB边上时，根据DB=DB1，即可解决问题，②当点B落在AC上时，在RT△DCB2中，根据∠C=90°，DB2=DB=2CD可以判定∠CB2D=30°，由此即可解决问题．
【详解】

①当点B落在AB边上时，
∵，
∴，
∴，
②当点B落在AC上时，
在中,
∵∠C=90°, ，
∴，
∴，
故选D.
【点睛】
本题考查的知识点是旋转的性质，解题关键是考虑多种情况，进行分类讨论.
6、D
【解析】
根据平均数、中位数、众数和方差的定义逐一求解可得．
【详解】
解：A、平均数为=3，正确；
B、重新排列为1、2、3、3、6，则中位数为3，正确；
C、众数为3，正确；
D、方差为×[（1-3）2+（6-3）2+（2-3）2+（3-3）2+（3-3）2]=2.8，错误；
故选：D．
【点睛】
本题考查了众数、平均数、中位数、方差．平均数平均数表示一组数据的平均程度．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量．
7、B
【解析】
根据俯视图中每列正方形的个数，再画出从正面看得到的图形即可．
【详解】
解：主视图，如图所示：
．
故选B．
【点睛】
本题考查由三视图判断几何体；简单组合体的三视图．用到的知识点为：主视图是从物体的正面看得到的图形；看到的正方体的个数为该方向最多的正方体的个数．
8、C
【解析】
试题分析：∵四边形ABCD中，∠ABC+∠BCD=360°﹣（∠A+∠D）=360°﹣α，
∵PB和PC分别为∠ABC、∠BCD的平分线，
∴∠PBC+∠PCB=（∠ABC+∠BCD）=（360°﹣α）=180°﹣α，
则∠P=180°﹣（∠PBC+∠PCB）=180°﹣（180°﹣α）=α．
故选C．
考点：1.多边形内角与外角2.三角形内角和定理．
9、B
【解析】
试题解析：从正面看是三个矩形，中间矩形的左右两边是虚线，
故选B.
10、B
【解析】
根据角平分线的定义推出△ECF为直角三角形，然后根据勾股定理即可求得CE2+CF2=EF2，进而可求出CE2+CF2的值．
【详解】
解：∵CE平分∠ACB，CF平分∠ACD，
∴∠ACE=∠ACB，∠ACF=∠ACD，即∠ECF=（∠ACB+∠ACD）=90°，
∴△EFC为直角三角形，
又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，
∴∠ECB=∠MEC=∠ECM，∠DCF=∠CFM=∠MCF，
∴CM=EM=MF=5，EF=10，
由勾股定理可知CE2+CF2=EF2=1．
故选：B．
【点睛】
本题考查角平分线的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线），直角三角形的判定（有一个角为90°的三角形是直角三角形）以及勾股定理的运用，解题的关键是首先证明出△ECF为直角三角形．
11、B
【解析】
比较OP与半径的大小即可判断.
【详解】
，，
，
点P在外，
故选B．
【点睛】
本题考查点与圆的位置关系，记住：点与圆的位置关系有3种设的半径为r，点P到圆心的距离，则有：点P在圆外；点P在圆上；点P在圆内.
12、B
【解析】
根据题意连接AD，再根据同弧的圆周角相等，即可计算的的大小.
【详解】
解：连接，

∵为的直径，
∴．
∵，
∴，
∴．
故选：B．
【点睛】
本题主要考查圆弧的性质，同弧的圆周角相等,这是考试的重点，应当熟练掌握.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、15π．
【解析】
试题分析：∵OB=BC=3，OA=4，由勾股定理，AB=5，侧面展开图的面积为：×6π×5=15π．故答案为15π．
考点：圆锥的计算．
14、
【解析】
根据圆周角定理可得∠BAC=∠BDC，然后求出tan∠BDC的值即可．
【详解】
由图可得，∠BAC=∠BDC，
∵⊙O在边长为1的网格格点上，
∴BE=3，DB=4，
则tan∠BDC==
∴tan∠BAC=
故答案为
【点睛】
本题考查的知识点是圆周角定理及其推论及解直角三角形，解题的关键是熟练的掌握圆周角定理及其推论及解直角三角形.
15、
【解析】
因为A点的坐标为（a，a），则C（a﹣1，a﹣1），根据题意只要分别求出当A点或C点在曲线上时a的值即可得到答案.
【详解】
解：∵A点的坐标为（a，a），
∴C（a﹣1，a﹣1），
当C在双曲线y=时，则a﹣1=，
解得a=+1；
当A在双曲线y=时，则a=，
解得a=，
∴a的取值范围是≤a≤+1．
故答案为≤a≤+1．
【点睛】
本题主要考查反比例函数与几何图形的综合问题，解此题的关键在于根据题意找到关键点，然后将关键点的坐标代入反比例函数求得确定值即可.
16、20
【解析】
先求出半径为30cm且圆心角为240°的扇形纸片的弧长，再利用底面周长=展开图的弧长可得．
【详解】
=40π．
设这个圆锥形纸帽的底面半径为r．
根据题意，得40π=2πr，
解得r=20cm．
故答案是：20.
【点睛】
解答本题的关键是有确定底面周长=展开图的弧长这个等量关系，然后由扇形的弧长公式和圆的周长公式求值．
17、2或﹣1
【解析】
解：当该点在﹣2的右边时，由题意可知：该点所表示的数为2，当该点在﹣2的左边时，由题意可知：该点所表示的数为﹣1．故答案为2或﹣1．
点睛：本题考查数轴，涉及有理数的加减运算、分类讨论的思想．
18、1
【解析】
设正多边形的边数为n，然后根据多边形的内角和公式列方程求解即可．
【详解】
解：设正多边形的边数为n，
由题意得，=144°，
解得n=1．
故答案为1．
【点睛】
本题考查了多边形的内角与外角，熟记公式并准确列出方程是解题的关键．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、1米．
【解析】
试题分析：作BE⊥DH，知GH=BE、BG=EH=10，设AH=x，则BE=GH=43+x，由CH=AHtan∠CAH=tan55°•x知CE=CH﹣EH=tan55°•x﹣10，根据BE=DE可得关于x的方程，解之可得．
试题解析：解：如图，作BE⊥DH于点E，则GH=BE、BG=EH=10，设AH=x，则BE=GH=GA+AH=43+x，在Rt△ACH中，CH=AHtan∠CAH=tan55°•x，∴CE=CH﹣EH=tan55°•x﹣10，∵∠DBE=45°，∴BE=DE=CE+DC，即43+x=tan55°•x﹣10+35，解得：x≈45，∴CH=tan55°•x=1.4×45=1．
答：塔杆CH的高为1米．

点睛：本题考查了解直角三角形的应用，解答本题要求学生能借助仰角构造直角三角形并解直角三角形．
20、（1）直线y=x+4，点B的坐标为（8，16）；（2）点C的坐标为（﹣，0），（0，0），（6，0），（32，0）；（3）当M的横坐标为6时，MN+3PM的长度的最大值是1．
【解析】
（1）首先求得点A的坐标，然后利用待定系数法确定直线的解析式，从而求得直线与抛物线的交点坐标；
（2）分若∠BAC=90°，则AB2+AC2=BC2；若∠ACB=90°，则AB2=AC2+BC2；若∠ABC=90°，则AB2+BC2=AC2三种情况求得m的值，从而确定点C的坐标；
（3）设M（a，a2），得MN=a2+1，然后根据点P与点M纵坐标相同得到x=，从而得到MN+3PM=﹣a2+3a+9，确定二次函数的最值即可．
【详解】
（1）∵点A是直线与抛物线的交点，且横坐标为-2，
,A点的坐标为（-2，1），
设直线的函数关系式为y=kx+b，
将（0，4），（-2，1）代入得
解得
∴y＝x＋4
∵直线与抛物线相交，

解得：x=-2或x=8，
当x=8时，y=16，
∴点B的坐标为（8，16）；
（2）存在．
∵由A(－2，1)，B(8，16)可求得AB2＝=325
.设点C(m，0)，
同理可得AC2＝(m＋2)2＋12＝m2＋4m＋5，
BC2＝(m－8)2＋162＝m2－16m＋320，
①若∠BAC＝90°，则AB2＋AC2＝BC2，即325＋m2＋4m＋5＝m2－16m＋320，解得m＝－；
②若∠ACB＝90°，则AB2＝AC2＋BC2，即325＝m2＋4m＋5＋m2－16m＋320，解得m＝0或m＝6；
③若∠ABC＝90°，则AB2＋BC2＝AC2，即m2＋4m＋5＝m2－16m＋320＋325，解得m＝32，
∴点C的坐标为(－，0)，(0，0)，(6，0)，(32，0)　
（3）设M(a，a2)，
则MN＝，
又∵点P与点M纵坐标相同，
∴x＋4＝a2，
∴x= ，
∴点P的横坐标为，
∴MP＝a－，
∴MN＋3PM＝a2＋1＋3(a－)＝－a2＋3a＋9＝－ (a－6)2＋1，
∵－2≤6≤8，
∴当a＝6时，取最大值1，
∴当M的横坐标为6时，MN＋3PM的长度的最大值是1
21、（1）①3，1；②最小值为3；（1）
【解析】
（1）①根据点Q与点P之间的“直距”的定义计算即可；
②如图3中，由题意，当DCO为定值时，点C的轨迹是以点O为中心的正方形（如左边图），当DCO＝3时，该正方形的一边与直线y＝－x＋3重合（如右边图），此时DCO定值最小，最小值为3；
（1）如图4中，平移直线y＝1x＋4，当平移后的直线与⊙O在左边相切时，设切点为E，作EF∥x轴交直线y＝1x＋4于F，此时DEF定值最小；
【详解】
解：（1）①如图1中，

观察图象可知DAO＝1＋1＝3，DBO＝1，
故答案为3，1．
②（i）当点C在第一象限时（），根据题意可知，为定值，设点C坐标为，则，即此时为3；
（ii）当点C在坐标轴上时（，），易得为3；
（ⅲ）当点C在第二象限时（），可得；
（ⅳ）当点C在第四象限时（），可得；
综上所述，当时，取得最小值为3；
（1）如解图②，可知点F有两种情形，即过点E分别作y轴、x轴的垂线与直线分别交于、；如解图③，平移直线使平移后的直线与相切，平移后的直线与x轴交于点G，设直线与x轴交于点M，与y轴交于点N，观察图象，此时即为点E与点F之间“直距”的最小值.连接OE，易证，∴，在中由勾股定理得，∴，解得，∴.

【点睛】
本题考查一次函数的综合题，点Q与点P之间的“直距”的定义，圆的有关知识，正方形的性质等知识，解题的关键是理解题意，学会利用新的定义，解决问题，属于中考压轴题．
失分原因
第（1）问 （1）不能根据定义找出AO、BO的“直距”分属哪种情形；
（1）不能找出点C在不同位置时， 的取值情况，并找到 的最小值第（1）问 （1）不能根据定义正确找出点E与点F之间“直距” 取最小值时点E、F 的位置；
（1）不能想到由相似求出GO的值
22、（1）；（2）.
【解析】
【分析】（1）根据题意可求得2个“－2”所占的扇形圆心角的度数，再利用概率公式进行计算即可得；
（2）由题意可得转出“1”、“3”、“－2”的概率相同，然后列表得到所有可能的情况，再找出符合条件的可能性，根据概率公式进行计算即可得.
【详解】（1）由题意可知：“1”和“3”所占的扇形圆心角为120°，
所以2个“－2”所占的扇形圆心角为360°－2×120°＝120°，
∴转动转盘一次，求转出的数字是－2的概率为＝；
（2）由（1）可知，该转盘转出“1”、“3”、“－2”的概率相同，均为，所有可能性如下表所示：
第一次 第二次
1
－2
3
1
(1，1)
(1，－2)
(1，3)
－2
(－2，1)
(－2，－2)
(－2，3)
3
(3，1)
(3，－2)
(3，3)
由上表可知：所有可能的结果共9种，其中数字之积为正数的的有5种，其概率为.
【点睛】本题考查了列表法或树状图法求概率，用到的知识点为：概率=所求情况数与总情况数之比．
23、1.
【解析】
直接利用绝对值的性质以及零指数幂的性质和负指数幂的性质分别化简得出答案．
【详解】
解：原式=﹣1++4﹣1﹣（﹣1）
=﹣1++4﹣1﹣+1
=1．
【点睛】
本题考查了实数的运算，零指数幂，负整数指数幂，解题的关键是掌握幂的运算法则.
24、 “石鼓阁”的高AB的长度为56m．
【解析】
根据题意得∠ABC=∠EDC=90°，∠ABM=∠GFH=90°，再根据反射定律可知：∠ACB=∠ECD，则△ABC∽△EDC，根据相似三角形的性质可得=，再根据∠AHB=∠GHF，可证△ABH∽△GFH，同理得=，代入数值计算即可得出结论.
【详解】
由题意可得：∠ABC=∠EDC=90°，∠ABM=∠GFH=90°，
由反射定律可知：∠ACB=∠ECD，
则△ABC∽△EDC，
∴=，
即=①，
∵∠AHB=∠GHF，
∴△ABH∽△GFH，
∴=，即=②，
联立①②，解得：AB=56，
答：“石鼓阁”的高AB的长度为56m．
【点睛】
本题考查了相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定与性质.
25、图形见解析
【解析】试题分析：（1）根据同弧所对的圆周角相等和直径所对的圆周角为直角画图即可；（2）延长AC交⊙O于点E ，利用（1）的方法画图即可.
试题解析：
如图①∠DBC就是所求的角；
如图②∠FBE就是所求的角

26、（1）证明见解析；（2）证明见解析.
【解析】
（1）由DE与AB垂直，BF与CD垂直，得到一对直角相等，再由ABCD为平行四边形得到AD=BC，对角相等，利用AAS即可的值；
（2）由平行四边形的对边平行得到DC与AB平行，得到∠CDE为直角，利用三个角为直角的四边形为矩形即可的值．
【详解】
解：（1）∵DE⊥AB，BF⊥CD，
∴∠AED=∠CFB=90°，
∵四边形ABCD为平行四边形，
∴AD=BC，∠A=∠C，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（AAS）；
（2）∵四边形ABCD为平行四边形，
∴CD∥AB，
∴∠CDE+∠DEB=180°，
∵∠DEB=90°，
∴∠CDE=90°，
∴∠CDE=∠DEB=∠BFD=90°，
则四边形BFDE为矩形．
【点睛】
本题考查1．矩形的判定；2．全等三角形的判定与性质；3．平行四边形的性质．
27、.（1）见解析（2）
【解析】
（1）根据网格结构找出点B、C旋转后的对应点B′、C′的位置，然后顺次连接即可.
（2）先求出AC的长，再根据扇形的面积公式列式进行计算即可得解.
【详解】
解：（1）△AB′C′如图所示：

（2）由图可知，AC=2，
∴线段AC旋转过程中扫过的扇形的面积.