2022年小升初数学仿真模拟卷（二）（有答案，带解析）

这是一份2022年小升初数学仿真模拟卷（二）（有答案，带解析），共13页。试卷主要包含了选择题，判断题，填空题，计算题，操作题，解答题等内容，欢迎下载使用。
2022年小升初数学仿真模拟卷（二）
姓名：__________ 班级：__________考号：__________

题号
一
二
三
四
五
六
总分
评分







一、选择题：
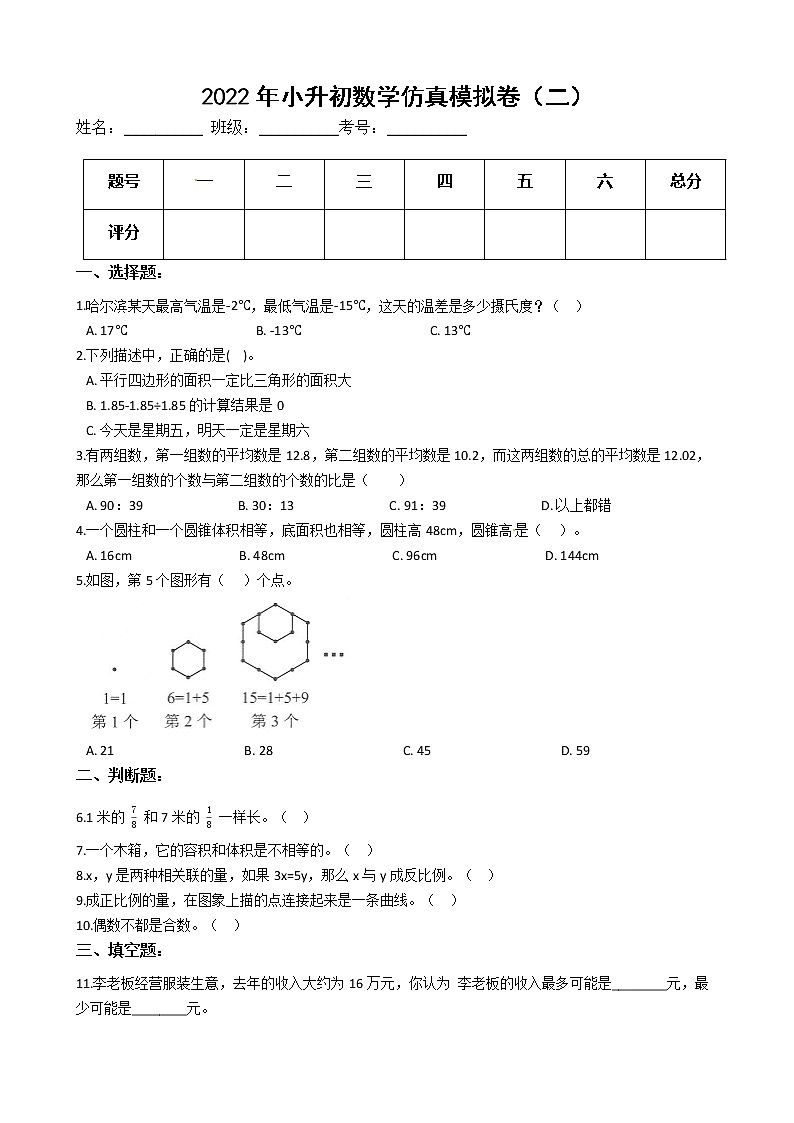
1.哈尔滨某天最高气温是-2℃，最低气温是-15℃，这天的温差是多少摄氏度？（   ）
A. 17℃                                        B. -13℃                                        C. 13℃
2.下列描述中，正确的是(    )。
A. 平行四边形的面积一定比三角形的面积大
B. 1.85-1.85÷1.85的计算结果是0
C. 今天是星期五，明天一定是星期六
3.有两组数，第一组数的平均数是12.8，第二组数的平均数是10.2，而这两组数的总的平均数是12.02，那么第一组数的个数与第二组数的个数的比是（　　）
A. 90：39                              B. 30：13                              C. 91：39                              D. 以上都错
4.一个圆柱和一个圆锥体积相等，底面积也相等，圆柱高48cm，圆锥高是（    ）。
A. 16cm                                 B. 48cm                                 C. 96cm                                 D. 144cm
5.如图，第5个图形有（    ）个点。

A. 21                                         B. 28                                         C. 45                                         D. 59
二、判断题：
6.1米的 78 和7米的 18 一样长。（   ）
7.一个木箱，它的容积和体积是不相等的。（   ）
8.x，y是两种相关联的量，如果3x=5y，那么x与y成反比例。（   ）
9.成正比例的量，在图象上描的点连接起来是一条曲线。（   ）
10.偶数不都是合数。（   ）
三、填空题：
11.李老板经营服装生意，去年的收入大约为16万元，你认为 李老板的收入最多可能是________元，最少可能是________元。
12.3÷________=________：24=25%= 12（） ________=________（填小数）
13.爸爸给汽车加了50升汽油，花了400元，总价与数量的比是________，比值是________．
14.有药液5L，用每瓶2.5mL的小瓶来分装，需要________小瓶。
15.甲数除以乙数商是 45 ，甲、乙两数的比是________；甲数是甲、乙两数和的________．
16.如图是一个圆柱体的侧面展开图，原来这个圆柱的体积可能是________或________cm3。( π 取3.14)

17.解比例 ．
29=8x，x=________
18.梨树和桃树棵数的比是8∶3．总份数是________，其中梨树的棵数占总棵数的________，桃树的棵数占总棵数的________．
19.一个圆柱底面半径5厘米，高6厘米．这个圆柱的底面积是________平方厘米，侧面积是________平方厘米，表面积是________平方厘米，体积是________立方厘米．与它等底等高的圆锥体积是________立方厘米．
四、计算题：
20.直接写出下面各题的得数。
5-0.28=       2.7×30=        4.5÷9=       0.27÷0.3=
21.怎样简便就怎样算。 
（1）8×7×1.25 （2）15 ×8.8+1.2× 15 （3）723-(325+123)






22.一块梯形苹果园，上底为85米，下底155米，高80米。苹果园的面积是多少公顷？每公顷可以收苹果8.5吨，这块地可以收苹果多少吨？






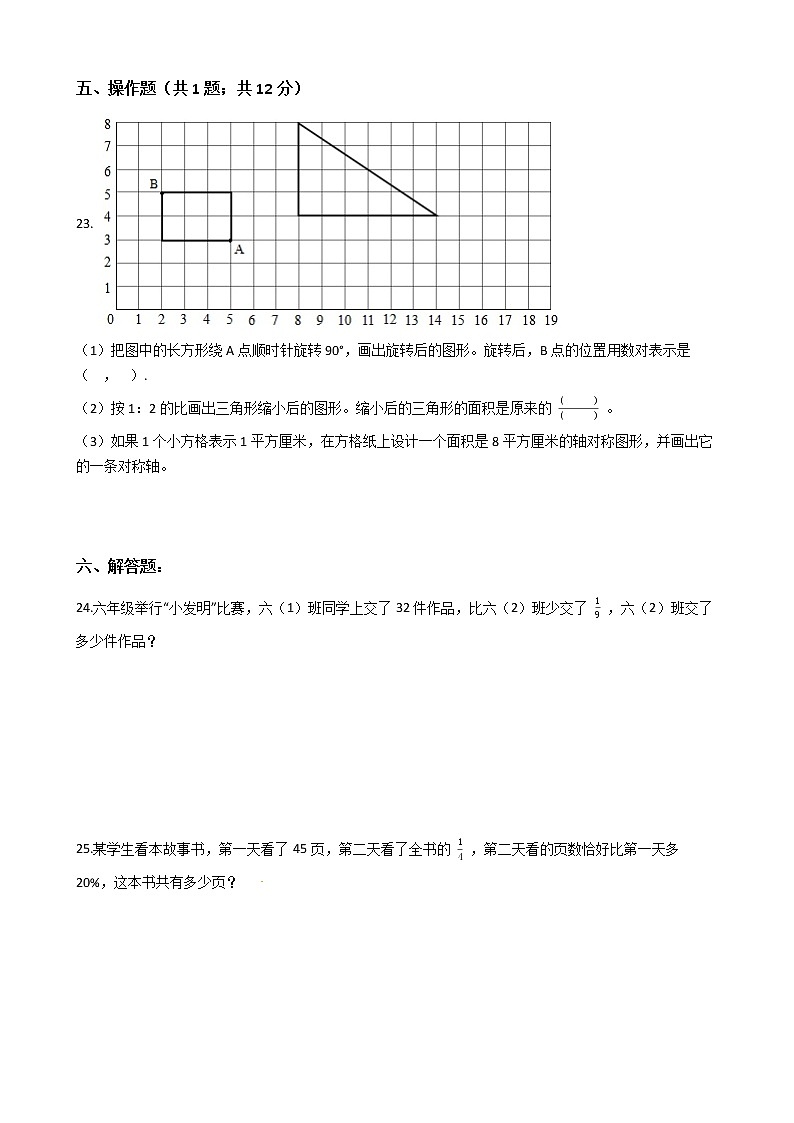
五、操作题（共1题；共12分）
23.
（1）把图中的长方形绕A点顺时针旋转90°，画出旋转后的图形。旋转后，B点的位置用数对表示是（   ，   ）.
（2）按1：2的比画出三角形缩小后的图形。缩小后的三角形的面积是原来的 ( )( ) 。
（3）如果1个小方格表示1平方厘米，在方格纸上设计一个面积是8平方厘米的轴对称图形，并画出它的一条对称轴。



六、解答题：
24.六年级举行“小发明”比赛，六（1）班同学上交了32件作品，比六（2）班少交了 19 ，六（2）班交了多少件作品？







25.某学生看本故事书，第一天看了45页，第二天看了全书的 14 ，第二天看的页数恰好比第一天多20%，这本书共有多少页？






26.已知一个内直径是8cm的饮料瓶内还剩饮料的高度是6cm，要解决“这个瓶子的容积是多少”这个问题，可以怎么解决?把你想到的办法表达清楚，不必解答。




27.在同一时间、同一地点，测得不同的树的高度与影长如下表所示。
树高/m
4
5
6
7
影长/m
2.4
3
3.6
4.2
（1）根据表中的数据，哪个量没有变？树高与影长成什么关系？
（2）如果在同一时间、同一地点，经测量，一座埃及金字塔的影长是88.2m，你能算出这座埃及金字塔的高度吗？





28.典典同学学完统计知识后，随机调查了她所在辖区若干名居民的年龄，并将调查的数据绘制成如下扇形和条形统计图。


请根据以上统计图提供的信息，解答下列问题。
（1）典典同学共调查了________名居民的年龄，扇形统计图中a=________，b=________。
（2）补全条形统计图。

答案解析部分
一、选择题
1.【答案】 C
【考点】正、负数的意义与应用
【解析】【解答】-2-（-15）=-2+15=13（℃）
故答案为：C。
【分析】根据题意可知，温差=最高气温-最低气温，据此列式解答。
2.【答案】 C
【考点】平行四边形的面积，简单事件发生的可能性求解，小数的四则混合运算，三角形的面积
【解析】【解答】解：A、平行四边形的面积和三角形的面积无法比较大小，此选项错误；
B、1.85-1.85÷1.85=1.85-1=0.85，此选项错误；
C、今天是星期五，明天一定是星期六，此选项正确。
故答案为：C。
【分析】A、不知道底和高，无法确定面积的大小；B、此题要先算除法，再算减法；C、今天星期五，明天星期六是一定的。
3.【答案】 C
【考点】平均数问题
【解析】【解答】解：把总个数当作“1”，可设第一组为x则：
12.8x+10.2×（1﹣x）=12.02
   12.8x+10.2﹣10.2x=12.02
               2.6x=1.82
                  x=91130
则第二组为：1﹣91130=39130 ，
它们的比为：91130：39130=91：39．
故选：C．
【分析】根据本题中所给的数量关系，如果第一组数和第二组数的总个数为“1”的话，可设第一组为x，那么第二组就为（1﹣x），由此可得方程：12.8x+10.2×（1﹣x）=12.02．
4.【答案】 D
【考点】圆柱与圆锥体积的关系
【解析】【解答】解：48×3=144（cm）
故答案为：D。
【分析】一个圆柱和一个圆锥体积相等，底面积也相等，则圆锥的高=圆柱的高×3。
5.【答案】 C
【考点】数形结合规律
【解析】【解答】 如图，第5个图形有2×52-5=45个点。
故答案为：C。
【分析】观察图可以得到规律：第n个图形有2n2-n个点，据此规律列式解答。
二、判断题
6.【答案】 正确
【考点】分数与整数相乘
【解析】【解答】1×78=78（米）；
7×18=78（米）；
78米=78米，原题说法正确.
故答案为：正确.
【分析】根据分数乘法的意义，求一个数的几分之几是多少，用乘法计算，据此计算出结果再比较大小即可.
7.【答案】 正确
【考点】体积和容积的关系
【解析】【解答】解：木箱有厚度，所以木箱的容积小于它的体积，原题说法正确。
故答案为：正确
【分析】木箱的容积是所能容纳物体的体积，木箱的体积是木箱所占空间的大小，容积是从内部测量的数据计算的，体积是从外部测量的数据计算的，除去木箱的厚度，木箱的体积是大于容积的。
8.【答案】 错误
【考点】成正比例的量及其意义，成反比例的量及其意义
【解析】【解答】 3x=5y， 则yx=35 ， 比值一定， 那么x与y成反比例。 原说法错误。
故答案为：错误。
【分析】两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。 
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，他们的关系叫做反比例关系。
9.【答案】 错误
【考点】成正比例的量及其意义
【解析】【解答】解：成正比例的量，在图象上描的点连接起来是一条经过原点的直线，本题说法错误．
故答案为：错误．
【分析】成正比例的两种量是对应的比值一定，也就是说一种量变化，另一种量也随着变化，它们的变化方向相同，所以成正比例的量，在图象上描的点连接起来是一条直线．
10.【答案】 正确
【考点】奇数和偶数，合数与质数的特征
【解析】【解答】2是偶数，但是2不是合数，所以偶数不都是合数。说法正确。
故答案为：正确。
【分析】除2以外的偶数都是合数。
三、填空题
11.【答案】 164999；155000
【考点】亿以内数的近似数及改写
【解析】【解答】解：李老板的收入最多可能是164999元，最少可能是155000元。
故答案为：164999；155000。
【分析】从题中看出，李老板的收入是近似数，所以对原数的千位进行四舍五入即可。
12.【答案】 12；6；48；0.25
【考点】比与分数、除法的关系
【解析】【解答】解：3÷25%=12；24×25%=6；12÷25%=48；25%=0.25.
故答案为：12；6；48；0.25.
【分析】除数=被除数÷商；比的前项=比的后项×比值；分母=分子÷分数值；百分数化小数，把小数点向左移动两位，同时把百分号去掉。
13.【答案】 8：1；8
【考点】比的化简与求值
【解析】【解答】解：总价与数量的比是：400：50=8：1；比值：8÷1=8.
故答案为：8：1；8
【分析】400元是总价，50升是数量，写出总价与数量的比并化成最简整数比；用化简后的比的前项除以后项求出比值.
14.【答案】 2000

【考点】容积单位间的进率及换算
【解析】【解答】解：5L=5000mL，需要5000÷2.5=2000小瓶。
故答案为：2000。
【分析】需要小瓶的瓶数=药液的容积÷每个小瓶的容积。
15.【答案】 4:5；49
【考点】比的应用
【解析】【解答】解：设甲数为4，则乙数为5，甲数：乙数＝4：5；
甲数是甲、乙两数和的 44+5 ＝ 49 。
故答案为：4：5； 49 。
【分析】甲数除以乙数的商是45 ， 就可以把甲数看作4，乙数看作5，写出甲数与乙数的比即可；用甲数除以甲、乙两数的和即可求出甲数是甲、乙两数和的几分之几。
16.【答案】 42.39；27.26
【考点】圆柱的展开图，圆柱的体积（容积）
【解析】【解答】9.42÷3.14÷2=1.5（cm）；3.14×1.5×1.5×6=42.39（cm³）；
6÷3.14÷2≈0.96（cm）；3.14×0.96×0.96×9.42≈27.26（cm³）。
故答案为：42.39；27.26。
【分析】分两种情况考虑：
第一种情况：9.42是底面周长，6是高；
第二种情况：6是底面周长，9.42是高；
底面周长÷3.14÷2=底面半径，π×底面半径的平方×高=圆柱体积。
17.【答案】 36
【考点】应用比例的基本性质解比例
【解析】【解答】29=8x
      解：2x=9×8
            2x=72
        2x÷2=72÷2
              x=36
故答案为：36.
【分析】解比例的依据是比例的基本性质：在比例里，两外项之积等于两内项之积，据此解答.
18.【答案】 11；811；311
【考点】应用比例解决实际问题
【解析】【分析】梨树所占的分数和桃树所占的分数分别为8份和3份，所以总分数是：8+3=11，一个数占总数的几分之几等于这个数的份数除以总份数。

19.【答案】 78.5；188.4；345.4；471；157
【考点】圆柱的侧面积、表面积，圆柱的体积（容积），圆柱与圆锥体积的关系
【解析】【解答】3.14×52=78.5（平方厘米）；3.14×5×2×6=188.4（平方厘米）；188.4+78.5×2=345.4（平方厘米）；78.5×6=471（立方厘米）；471×13=157（立方厘米）
【分析】圆柱的侧面积=底面周长×高，圆柱的底面积=πr2 ， 圆柱的表面积=侧面积+底面积×2，圆柱的体积=底面积×高，和它等底等高的圆锥体的体积是它的13；据此解答。
四、计算题
20.【答案】 5-0.28=4.72     2.7×30=81     4.5÷9=0.5      0.27÷0.3=0.9
【考点】小数乘整数的小数乘法，除数是小数的小数除法
【解析】【分析】计算小数减法时要把小数点对齐；计算小数乘法时要注意乘积中小数点的位置；计算除数是小数的除法时要把除数转化成整数再计算。
21.【答案】 （1）解：8×7×1.25
=8×1.25×7
=10×7
=70

（2）解：15×8.8+1.2×15
=15×(8.8+1.2)
=15×10
=2

（3）解：723-(325+123)
=723-325-123
=723-123-325
=600-325
=275

【考点】1000以内数的连减运算，小数乘法运算律，分数乘法运算律
【解析】【分析】(1)运用乘法交换律先计算8×1.25；(2)运用乘法分配律简便计算；(3)去掉括号后先算723-123，这样计算比较简便.
22.【答案】 解：面积=（85+155）×80÷2
=240×80÷2
=19200÷2
=9600（平方米）
=0.96公顷
8.5×0.96=8.16（吨）
答： 苹果园的面积是0.96公顷，每公顷可以收苹果8.5吨，这块地可以收苹果8.16吨。解：9600平方米=0.96公顷，8.16吨
【考点】梯形的面积，小数乘小数的小数乘法，公顷、平方千米与平方米之间的换算与比较
【解析】【分析】梯形的面积=（上底+下底）×高÷2，代入数值即可计算出苹果园的面积，再利用1公顷=10000平方米化成公顷数，再根据苹果的总吨数=每公顷收苹果的吨数×果园的公顷数，代入数值计算即可。
五、操作题
23.【答案】 （1）解：绕点A顺时针旋转90°得到图形1，如下图所示：

此时点B的位置为（7，6）。

（2）解：三角形按1：2的比例缩小后得到图形2，如下图所示：

三角形的面积=底×高÷2，底与高都缩小到原来的12 ， 则面积缩小到原来的12×12=14。

（3）解：如图，图形3的面积是8平方厘米，它是一个长方形，它的对称轴有2条，分别是对边中点所在的直线。

【考点】轴对称图形的对称轴数量及位置，图形的缩放，数对与位置，作旋转后的图形
【解析】【分析】（1）画旋转图形的方法：把图形的每个点与旋转中心连接，再量出题目要求旋转的角度，最后依次连接；
用数对表示位置的方法是：第一个数字表示列，第二个数字表示行，中间用“，”隔开，据此解答；
（2）根据题意可知，先数一数原来直角三角形的两条直角边的格数，然后分别缩小到原来的12 ， 即可画出三角形缩小后的图形，三角形的面积=底×高÷2，当底和高都缩小到原来的12 ， 则缩小后的三角形的面积是原来的12×12=14；
（3）根据题意可知，可以画一个长是4厘米，宽是2厘米的长方形，它的面积是8平方厘米，然后连接两条长的中点所在的直线就是它的一条对称轴，据此作图。
六、解答题
24.【答案】 解：32÷（1- 19 ）=36（件）
答：六（2）班交了36件作品。
【考点】分数除法与分数加减法的混合运算，分数除法的应用
【解析】【分析】六（2）班交作品的件数=六（1）班同学上交作品的件数÷（1-六（1）班比六（2）班少交了几分之几），据此代入数据作答即可。
25.【答案】 解：45×（1+20%）÷14
=54×4
=216（页）
答： 这本书共有216页。
【考点】分数四则混合运算及应用，百分数的应用--运用除法求总量
【解析】【分析】总页数= 第一天所看页数×（1+20%）÷第二天所看页数的占比。
26.【答案】 解：已知一个内直径是8cm的饮料瓶内还剩饮料的高度是6cm，可求瓶中剩下饮料的体积，然后盖紧瓶盖并将饮料瓶倒置，量出此时饮料液面到瓶底空的部分的高度，可求瓶中空的部分的容积，加上瓶中剩余饮料的体积即是这个瓶子的容积。
【考点】圆柱的体积（容积），体积的等积变形
【解析】【分析】此题主要考查了圆柱体积的应用，根据题意可知，已知一个内直径是8cm的饮料瓶内还剩饮料的高度是6cm，可求瓶中剩下饮料的体积，然后盖紧瓶盖并将饮料瓶倒置，量出此时饮料液面到瓶底空的部分的高度，可求瓶中空的部分的容积，加上瓶中剩余饮料的体积即是这个瓶子的容积。
27.【答案】 （1）解：树高与影长的比值没有变，树高与影长成正比例。
（2）解：设这座埃及金字塔高xm。
x88.2=42.4
         x=147
【考点】正比例应用题，应用比例解决实际问题
【解析】【分析】（1）影长树高=6，所以树高与影长的比值没有变，两个量的比值不变，所以树高与影长成正比例；
（2）本题可以用方程作答，即设这座埃及金字塔高xm，题中存在的比例关系是：这座埃及金字塔的高度这座埃及金字塔的影子的长度=影子长2.4m影子长2.4m所对应的树高 ， 据此代入数据和字母作答即可。
28.【答案】 （1）500；20%；12%
（2）500×22%=110人，所以条形统计图是：


【考点】单式条形统计图的特点及绘制，从扇形统计图获取信息，百分数的应用--运用除法求总量
【解析】【解答】解：（1）230÷46%=500人，所以典典同学共调查了500名居民的年龄；
100÷500=20%，所以a=20%；
b=1-22%-46%-20%=12%。
【分析】（1）调查的人数=15~40岁的人数÷15~40岁占的百分数；a=0~14岁的人数÷调查的人数；b=1-15~40岁占的百分数-41~60岁占的百分数-a。
（2）41~60岁的人数=调查的人数×41~60岁占的百分数，据此做图即可。