尺规作图学案无答案

学员编号：                                年    级：                    课 时 数：

学员姓名：                                辅导科目：                    学科教师：

课程主题：尺规作图

授课时间：

学习目标

掌握稍微复杂的作图

教学内容

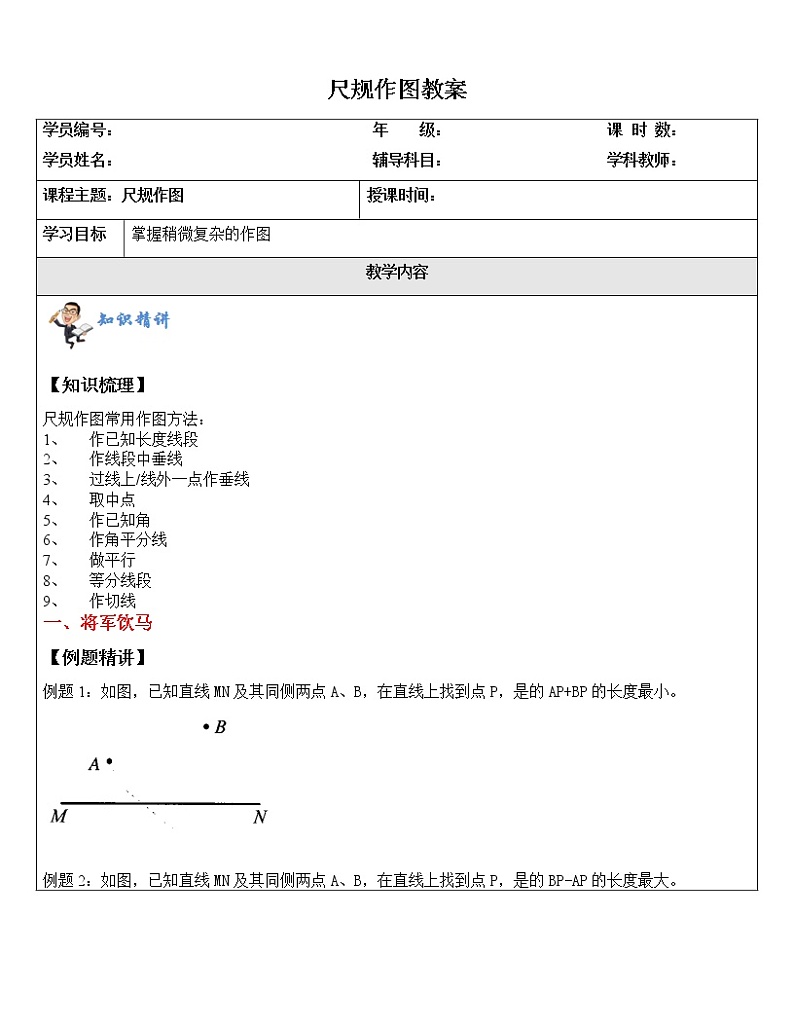
【知识梳理】

尺规作图常用作图方法：

1、  作已知长度线段

2、  作线段中垂线

3、  过线上/线外一点作垂线

4、  取中点

5、  作已知角

6、  作角平分线

7、  做平行

8、  等分线段

9、  作切线

一、将军饮马

【例题精讲】

例题1：如图，已知直线MN及其同侧两点A、B，在直线上找到点P，是的AP+BP的长度最小。

例题2：如图，已知直线MN及其同侧两点A、B，在直线上找到点P，是的BP-AP的长度最大。

例题3：如图，已知两点P在锐角∠AOB内，分别在OA、OB上求点M、N，使PM＋MN＋NP最短．
 

例题4：如图，已知两点P、Q在锐角∠AOB内，分别在OA、OB上求点M、N，使PM＋MN＋NQ最短．
 

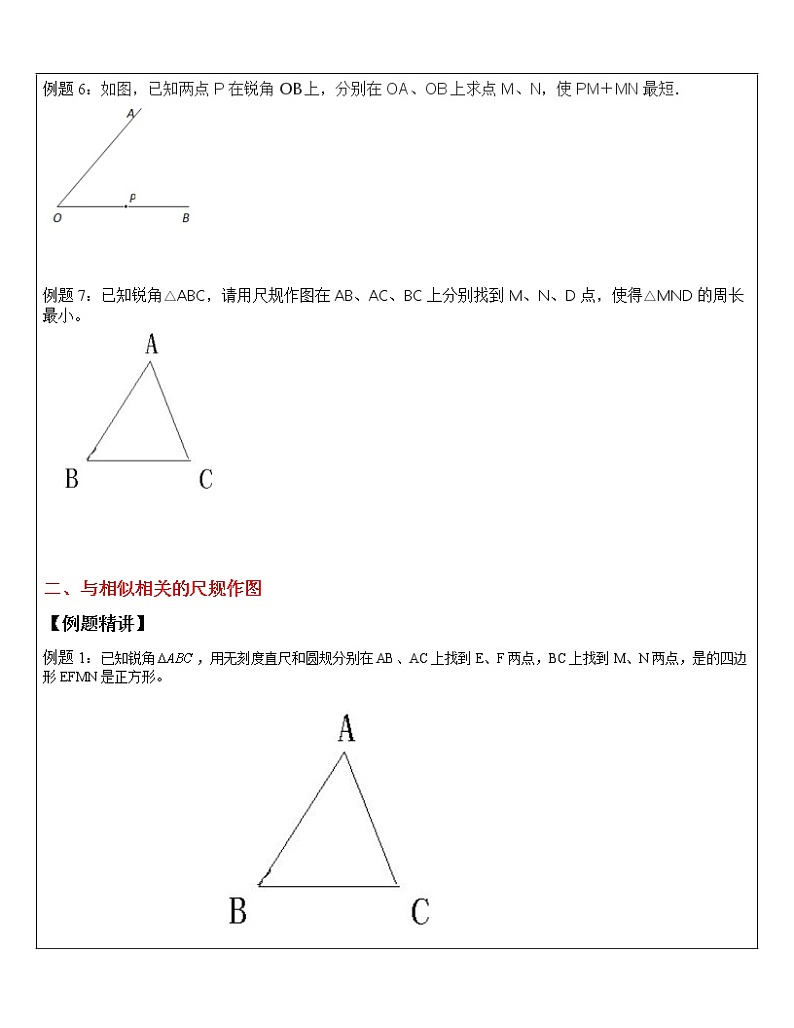
例题5：如图，已知两点P在锐角∠AOB内，分别在OA、OB上求点M、N，使PM＋MN最短．
 

例题6：如图，已知两点P在锐角OB上，分别在OA、OB上求点M、N，使PM＋MN最短．
 

例题7：已知锐角△ABC，请用尺规作图在AB、AC、BC上分别找到M、N、D点，使得△MND的周长最小。

二、与相似相关的尺规作图

【例题精讲】

例题1：已知锐角，用无刻度直尺和圆规分别在AB、AC上找到E、F两点，BC上找到M、N两点，是的四边形EFMN是正方形。

例题2：已知锐角，用无刻度直尺和圆规在AB、AC上分别找到M、N点，使得BM=MN=CN。

三、无刻度的三角板直尺作图

【例题精讲】

例题1：已知四边形ABCD，O为对角线BD中点，试用无刻度的直尺三角板按下列要求作图：

（1）过A点作直线平分四边形ABCD的面积

（2）过P点作直线平分四边形ABCD的面积

、如图，在四边形中，//，，为的中点，请仅用无刻度直尺分别按下列要求画图（保留画图痕迹）.

（）在图中，画出的边上的中线；

（）在图中，若，画出的边上的高.

、请仅用无刻度的直尺在下列图和图中按要求画菱形。

()图是矩形，，分别是和的中点，以为边画一个菱形；

()图是正方形,是对角线上任意一点(>)，以为边画一个菱形。

仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)

(1)如图，画出⊙的一个内接矩形；

(2)如图,AB是⊙的直径,是弦,且，画出⊙的内接正方形。

如图，在中，

（）作出经过点,圆心在斜边上且与边相切于点的⊙(要求：用尺规画图，保留作图痕迹，不写作法和证明)

（）设（）中所作的⊙与边交于异于点的另外一点,若⊙的直径为5，;求的长。（如果用尺规作图画不出图形，可画出草图完成（）问）

5. 已知，如图，线段AB，利用无刻度的直尺和圆规，作一个满足条件的ABC：①为直角②

                    A                   B  

6. 如图，已知点D、E分别在的边，已知，

⑴请用直尺和圆规在画出点D和点E，并证明所作的线段DE符合题目要求

⑵若，请求出的长  

7.如图，已知,请利用没有刻度的直尺和圆规按下列要求作图

（1）       做出的内心;

（2）       在（1）的条件下，请分别在边上找点使得∠,且同时满足的周长恰好等于边的长度和.

8.（1）在面积的最大值是                 

（2）已知：和线段，用无刻度的直尺和圆规求作,使且边上的高为a（注：不写做法，保留作图痕迹，对图中涉及到的点用字母进行标注，作出一个符合题意的三角形即可）

9.如图，已知（），请用直尺（不带刻度）和圆规，按下列要求作图

（1）在边上确定一点，使得；

（2）作出一个，使得：①是直角三角形；②的周长等于边的长。

10. 如图，已知矩形，是上一点，

（1）利用尺规分别在上确定点，使得四边形是特殊的平行四边形；（提示：①保留作图痕迹，不写做法；②只需作出一种情况即可.）

（2）在（1）的条件下，若，则所做四边形的周长为         .

11.（1）如图1，已知垂直平分，垂足为，与相交于点，连接，求证：。

（2）如图2，在中，，为的中点。

①用直尺和圆规在边上求作点，使得（保留作图痕迹，不要求写作法）。

②在①的条件下，如果，那么是的中点吗？为什么？

12.           如图，已知矩形，，，点为线段上任一点 
    若，请在图中用尺规作图画出符合要求的点；（保留作图痕迹，不要求写作法） 
    若符合中要求的点必定存在，求的取值范围． 

、已知在四边形中，是边上一点，且~.分别在图和图②中用直尺和圆规作出所有满足条件的点.（保留作图痕迹，不写作法）

（）如图，四边形是矩形；

（）如图②，四边形中，

14.背景：（1）经过三角形定点，并且将该三角形的面积等分的直线有______条；

（2）如图①，直线，依据____________________________（填定理），可得与面积相等.

解决：如图②，四边形中，与不平行，,且，过点画出四边形的面积等分线，无需尺规作图，但需要写出画法.

图①                                        图②