期末测试卷04-新教材2020-2021学年高一数学下学期期末考试全真模拟卷（人教A版2019）

2020-2021学年高一数学下学期期末考试全真模拟卷（四）

测试时间：120分钟 测试范围：人教A2019必修第一册+第二册 满分：150分

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.

3．考试结束后，将本试卷和答题卡一并交回.

一、单项选择题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1、已知集合，则（   ）

 A．  B．

 C．  D．

【答案】C

【详解】

由题意得，，则

．故选C．

2、若，则（   ）

 A．0 B．1 C． D．2

【答案】C

【详解】

因为，所以．

故选：C．

3、设，则“”是“”的（   ）

 A．充分不必要条件  B．必要不充分条件

 C．充要条件  D．既不充分也不必要条件

【答案】A

【详解】

求解二次不等式可得：或，

据此可知：是的充分不必要条件.

故选：A.

4、，则的大小关系为（   ）

 A． B． C． D．

【答案】D

【详解】

因为，

，

，

所以.

故选：D.

5、如图，点为正方形的中心，为正三角形，平面平面是线段的中点，则（   ）

 A．，且直线是相交直线

 B．，且直线是相交直线

 C．，且直线是异面直线

 D．，且直线是异面直线

【答案】B

【详解】

如图所示， 作于，连接，过作于．

连，平面平面．

平面，平面，平面，

与均为直角三角形．设正方形边长为2，易知，

．，故选B．

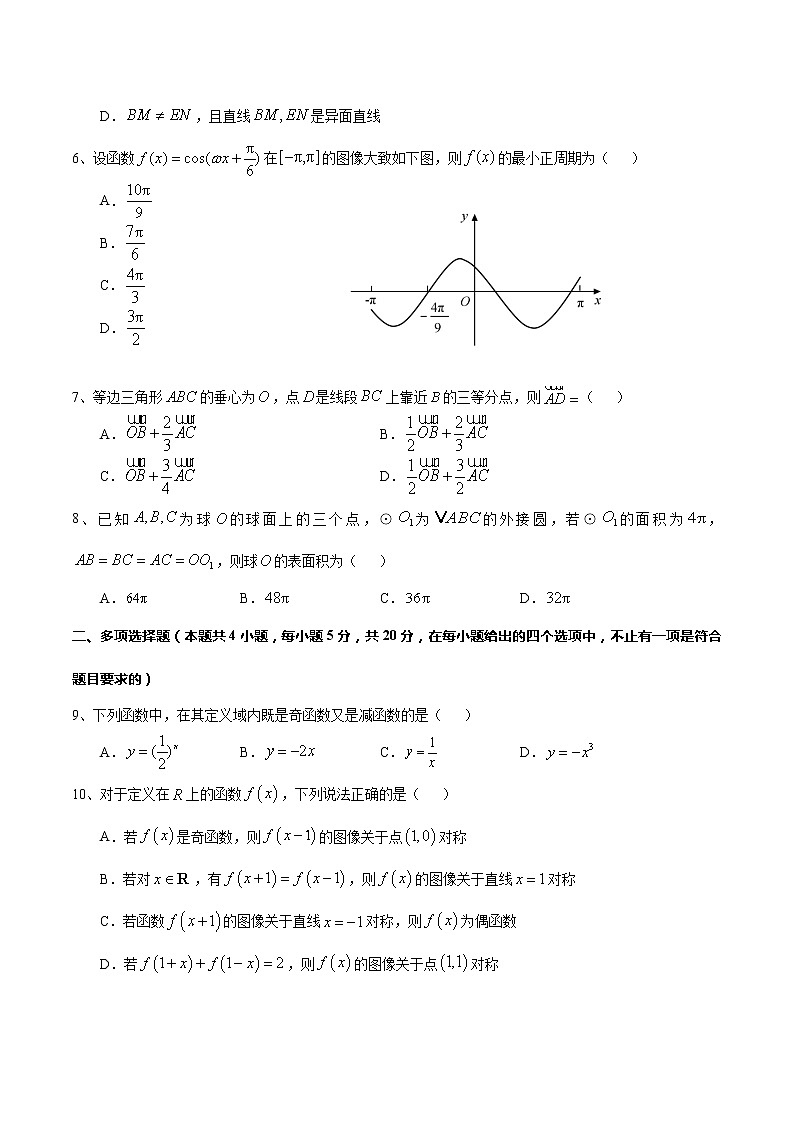
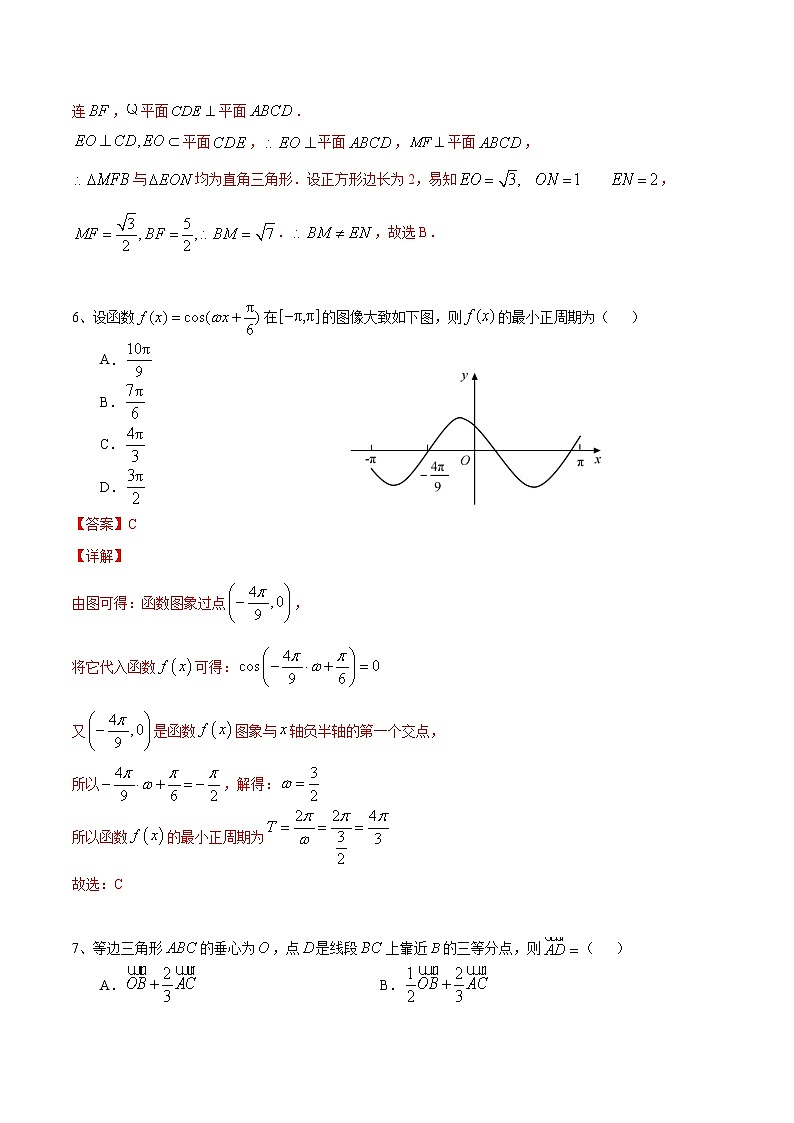
6、设函数在的图像大致如下图，则的最小正周期为（   ）

A．

B．

 C．

 D．

【答案】C

【详解】

由图可得：函数图象过点，

将它代入函数可得：

又是函数图象与轴负半轴的第一个交点，

所以，解得：

所以函数的最小正周期为

故选：C

7、等边三角形的垂心为，点是线段上靠近的三等分点，则（   ）

 A．  B．

 C．  D．

【答案】A

【详解】

如图所示：

延长交于点，

因为为等边三角形的垂心，所以为的中点，

所以

.

故选：A

8、已知为球的球面上的三个点，⊙为的外接圆，若⊙的面积为，，则球的表面积为（   ）

 A． B． C． D．

【答案】A

【详解】

设圆半径为，球的半径为，依题意，

得，为等边三角形，

由正弦定理可得，

，根据球的截面性质平面，

，

球的表面积.

故选：A

二、多项选择题（本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，不止有一项是符合题目要求的）

9、下列函数中，在其定义域内既是奇函数又是减函数的是（   ）

 A． B． C． D．

【答案】BD

【详解】

A，函数是非奇非偶函数，故排除A；B，函数是上的奇函数也是减函数，故B正确；C，函数在定义域上是奇函数，但在和上是减函数，在定义域上不具有单调性，故排除C；D，函数是上的奇函数也是减函数，故D正确.

故选：BD

10、对于定义在上的函数，下列说法正确的是（   ）

 A．若是奇函数，则的图像关于点对称

 B．若对，有，则的图像关于直线对称

 C．若函数的图像关于直线对称，则为偶函数

 D．若，则的图像关于点对称

【答案】ACD

【详解】

对A，是奇函数，故图象关于原点对称，

将的图象向右平移1个单位得的图象，

故的图象关于点（1，0）对称，正确；

对B，若对，有，

得，所以是一个周期为2的周期函数，

不能说明其图象关于直线对称，错误.；

对C，若函数的图象关于直线对称，

则的图象关于y轴对称，故为偶函数，正确；

对D，由得，

，

的图象关于（1，1）对称，正确.

故选：ACD.

11、设是两条不重合的直线，，，是三个不同的平面．下列四个命题中，正确的是（   ）

 A．若，，则 B．若，，则

 C．若，，则 D．若，，则

【答案】AC

【详解】

对于A，由面面垂直的判定可知是正确的；

对于B，观察教室的墙角共顶点的三个平面，发现与还可能相交，故B错误；

对于C,直线同时垂直平面，则直线与两平面所成的角均为，故两平面平行，故C正确；

对于D，直线b可能在平面内，故D错误．

故选：AC.

12、如图，直四棱柱的底面是边长为的正方形，侧棱长为，，分别是，的中点，过点，，的平面记为，则（   ）

 A．平面截直四棱柱所得截面的形状为四边形

B．平面截直四棱柱所得截面的面积为

 C．平面将直四棱柱分割成的上、下两部分的体积之比为

 D．点到平面的距离与点到平面的距离之比为

【答案】BC

【详解】

A：如图，延长分别与，的延长线交于点，，连接交于点，连接，交于点，连接，，则平面截直四棱柱所得截面为五边形，错误；

B：由平行线分线段成比例可得，，故，则△为等腰直角三角形，由相似三角形可知，

故，则，，连接，

易知，因此五边形可以分成等边三角形和等腰梯形，

等腰梯形的高，则等腰梯形的面积为，

又，所以五边形的面积为．正确；

C：记平面将直四棱柱分割成的上、下两部分的体积分别为，，则，所以，则，正确；

D：平面过线段的中点，所以点到平面的距离与点到平面的距离相等，

由平面过的三等分点可知，点到平面的距离是点到平面的距离的2倍，

因此点到平面的距离是点到平面的距离的2倍，错误．

故选：BC.
 

三、填空题（本题共4小题，每小题5分，共20分）

13、平面向量与的夹角为，且，，则________．

【答案】2

【详解】

因为，

所以，

又因为与的夹角为，，

所以，

所以

故答案为：2

14、的内角的对边分别为，已知，则___________.

【答案】.

【详解】

由正弦定理，得．，得，即，故选D．

15、学生到工厂劳动实践，利用打印技术制作模型.如图，该模型为长方体挖去四棱锥后所得的几何体，其中为长方体的中心，分别为所在棱的中点，，打印所用原料密度为，不考虑打印损耗，制作该模型所需原料的质量为___________.

【答案】118．8

【详解】

由题意得， ，

四棱锥O−EFG的高3cm， ∴．

又长方体的体积为，

所以该模型体积为，

其质量为．

16、设函数的定义域为，满足，且当时，.若对任意，都有，则的取值范围为_________________.

【答案】

【详解】

时，，，，即右移1个单位，图像变为原来的2倍．

如图所示：当时，，令，整理得：，（舍），时，成立，即，.

四、解答题（17题10分，其余每题12分，共70分，解答应写出文字说明、证明过程或演算步骤，考生根据要求作答）

17、某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图(如图所示)，其中样本数据分组区间为

（1）求频率分布直方图中的值；

（2）估计该企业的职工对该部门评分不低于80的概率；

（3）从评分在的受访职工中，随机抽取2人，求此2人评分都在的概率.

【答案】（1）；（2）；（3）.

【详解】

（1）因为，

所以

（2）由所给频率分布直方图知，50名受访职工评分不低于80的频率为，

所以该企业职工对该部门评分不低于80的概率的估计值为

（3）受访职工评分在[50，60)的有：50×0.006×10=3(人)，

即为；

受访职工评分在[40，50)的有： 50×0.004×10=2(人)，即为.

从这5名受访职工中随机抽取2人，所有可能的结果共有10种，它们是

又因为所抽取2人的评分都在[40，50)的结果有1种，即，

故所求的概率为

18、已知单位圆的内接的三个内角的对边分别为，若

（1）求角的大小；

（2）若的面积为，求的周长．

【答案】（1）；（2）

【详解】

（1）在中，，，

所以，

即，所以．

因为，所以．

，所以，

，由余弦定理得

由得，

所以的周长为．

19、如图所示，在四棱锥中中，底面是边长为的正方形，平面平面，与交于点．

（1）连接，试证明：；

（2）若是的中点，平面，求多面体的体积．

【答案】（1）证明见解析；（2）2.

【详解】

（1）证明：过点作，垂足为，∵平面平面，

平面平面，平面，∴平面．又平面，

∴．∵底面是正方形，∴．

而、平面．∴平面，结合图形知平面．

故．

（2）解析：∵为中点且平面，而、平面，

∴且，进而得．

另一方面整合得，即平面，平面，

则．由（1）知平面，平面，∴，

整合得，则平面，于是是四棱锥的高．

因为是的中点，则三棱锥的高为，由此．

进而．

20、已知函数.

（1）若，求的值.

（2）在中，角的对边分别是，且满足，求的取值范围.

【答案】（1）；（2）.

【详解】

（1）

由可得：.

.

（2）由余弦定理得：，整理可得：，

，，

又，，，

，则，

，即的取值范围为.

21、计算机考试分理论考试与实际操作两部分，每部分考试成绩只记“合格”与“不合格”，两部分考试都“合格”者，则计算机考试“合格”，并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为，，，在实际操作考试中“合格”的概率依次为，，，所有考试是否合格相互之间没有影响.

（1）假设甲、乙、丙三人同时进行理论与实际操作两项考试，谁获得合格证书的可能性最大？

（2）这三人进行理论与实际操作两项考试后，求恰有两人获得合格证书的概率.

【答案】（1）丙；（2）

【详解】

（1）设“甲获得合格证书”为事件A，“乙获得合格证书”为事件B，“丙获得合格证书”为事件C，则，，.

因为，所以丙获得合格证书的可能性最大.

（2）设“三人考试后恰有两人获得合格证书”为事件D，则.

22、如图1，在矩形中，是的中点，将沿折起，得到如图2所示的四棱锥，其中平面平面.

(1)证明：平面；

(2)设为的中点，在线段上是否存在一点，使得平面，若存在，求出的值；若不存在，请说明理由．

【答案】（1）证明见解析（2）线段上存在满足题意的点，且＝

【详解】

(1)证明连接BE，

∵ABCD为矩形且AD＝DE＝EC＝BC＝2，

∴∠AEB＝90°，即BE⊥AE，

又平面D1AE⊥平面ABCE，

平面D1AE∩平面ABCE＝AE，BE⊂平面ABCE，

∴BE⊥平面D1AE.

(2)解AM＝AB，取D1E的中点L，连接AL，FL，

∵FL∥EC，EC∥AB，∴FL∥AB且FL＝AB，

∴FL∥AM，FL=AM

∴AMFL为平行四边形，∴MF∥AL，

因为MF不在平面AD1E上， AL⊂平面AD1E，所以MF∥平面AD1E.

故线段AB上存在满足题意的点M，且＝.