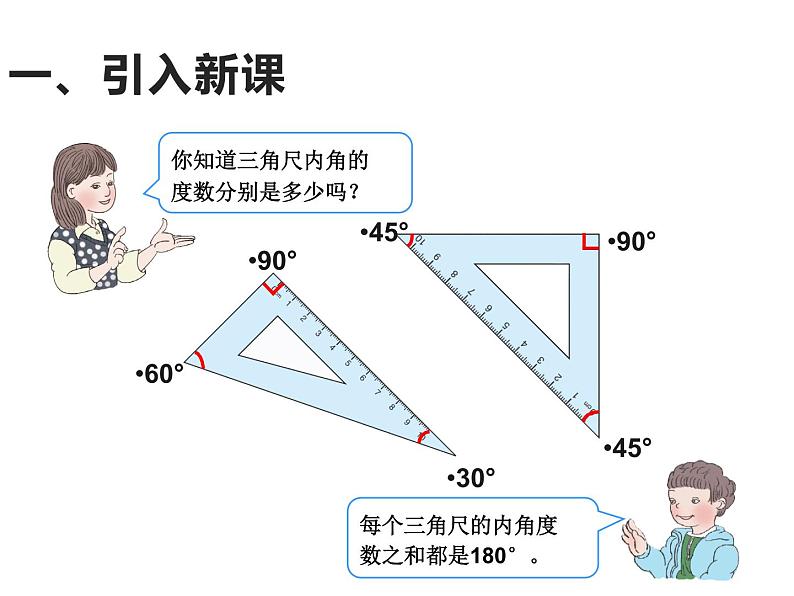
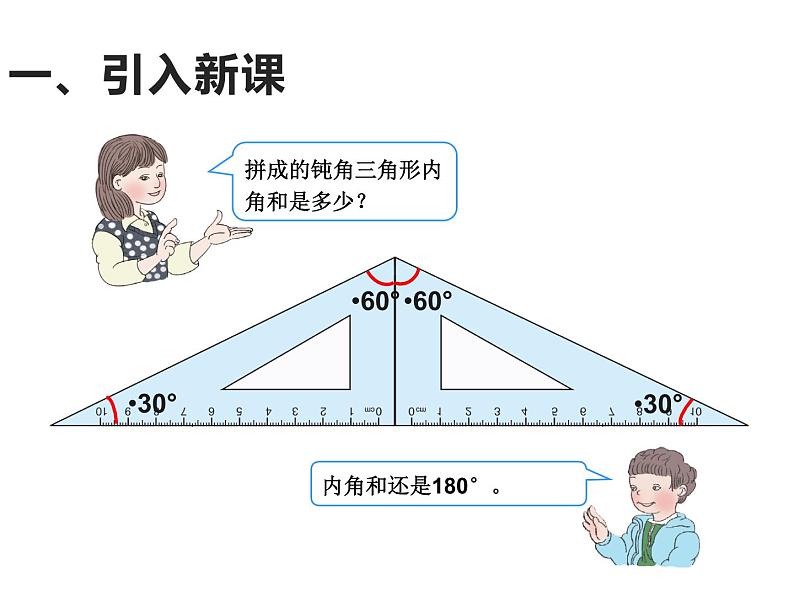
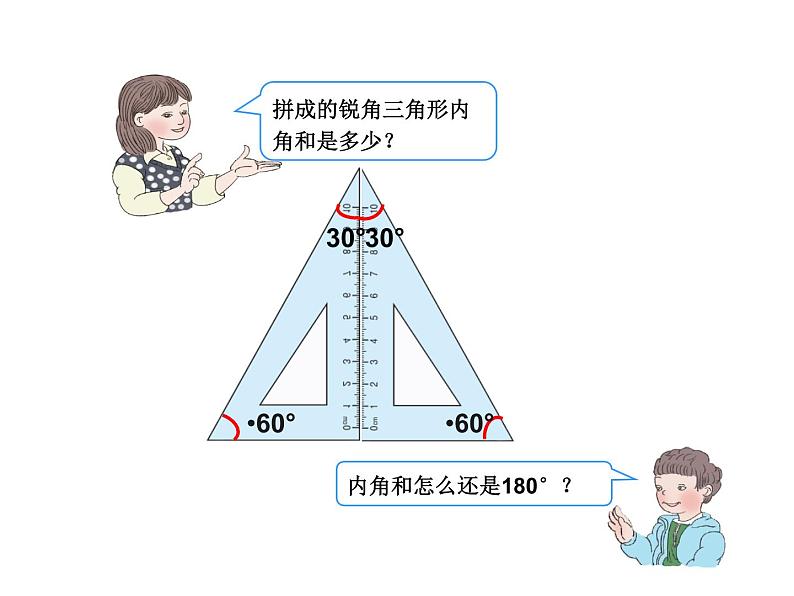
2021学年5 三角形三角形的内角和课堂教学课件ppt

这是一份2021学年5 三角形三角形的内角和课堂教学课件ppt，共17页。PPT课件主要包含了引入新课，活动要求，探究新知，拼一拼，平角180°，折一折，拓展方法，练习巩固，°÷3＝60°，拓展延伸等内容，欢迎下载使用。

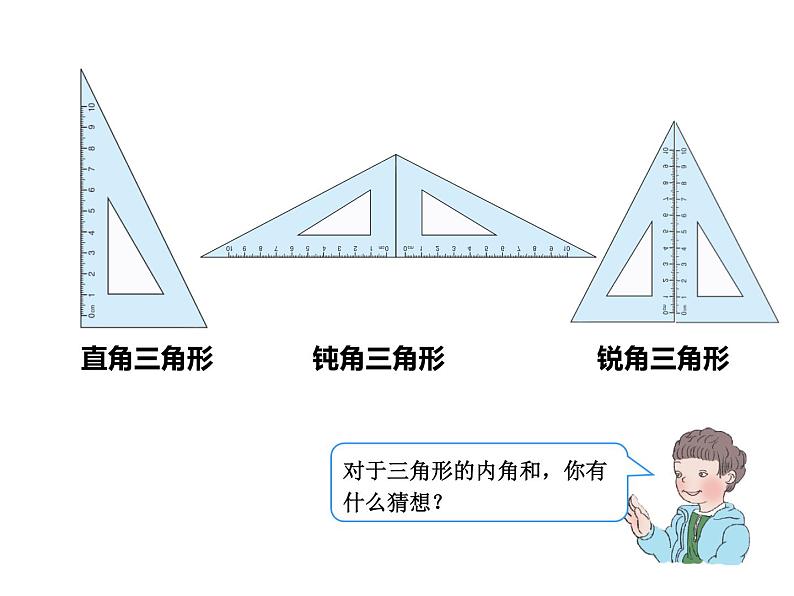
1. 请同学们拿出课前准备好的三角形纸片，每位 同学在锐角三角形、直角三角形、钝角三角形 中任选一种三角形。2. 选择合适的工具，验证自己的猜想。3. 独立完成后，把研究结果贴在展示板上，在小组 内交流汇报验证结果。比一比哪个组的方法多？
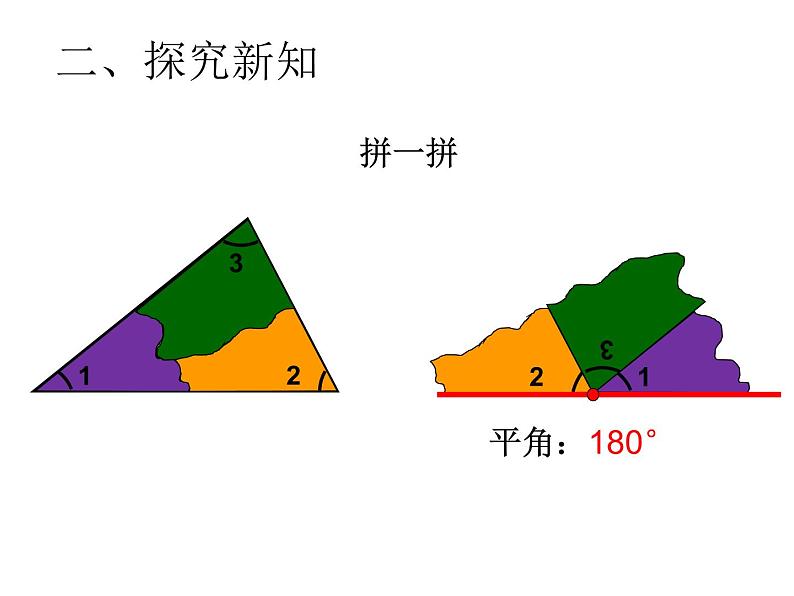
任意三角形的内角和是180°。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°，因此两个直角三角形的内角和应为：180°×2＝360°。
而直角三角形的两个直角不属于分割前三角形的内角，因此任意三角形的内角和应为：360°－180°＝180°。
三角形的内角和是180 °
同学们，我们刚才用不同的方法、不同的三角形研究了三角形的内角和，得到了一个相同的发现：
（1）三角形越大，它的内角和就越大。 （ ）（2）一个三角形的三个内角度数是：70°,64°,45°。（ ）（3）一个三角形至少有两个角是锐角。 （ ）（4）钝角三角形的内角和大于锐角三角形的内角和。 （ ）
1. 请你来当数学小判官。
2. 在一个三角形中，∠1＝120°,∠3＝35°, 求∠2的度数。
180°－120°－35°＝25°
1. 求出三角形各个角的度数。
（180°－96°）÷2 = 42°
2. 求出等腰三角形底角的度数。
90°－40°＝50°
3. 求出直角三角形另一个 锐角的度数。
4. 一个三角形可能有两个直角吗？一个 三角形可能有两个钝角吗？