2021学年27.2.2 相似三角形的性质精练

27.2.2 相似三角形的性质

一、单选题

1．如图，正方形ABCD的边长为4，G是BC边上一点，若矩形DEFG的边EF经过点A，GD＝5，则FG长为（　　）

A．2.8 B．3 C．3.2 D．4

【答案】C

【解析】

 解：∵G是边长为4的正方形ABCD边上一点，矩形DEFG的边EF经过点A，GD＝5，

∴∠C＝∠E＝90°，∠EDG＝∠ADC＝90°，ED＝FG，AD＝CD＝4，

∴∠EDA＝∠CDG，

∴△EDA∽△CDG，

∴，

即，

解得，ED＝3.2，

∴FG＝3.2，

故选：C．

 2．如图，在△ABC中，AB＝AC＝10，BC=12，正方形DEFG的顶点E，F在△ABC内，D、G分别在AB，AC上，DG＝3，则点F到BC的距离为（ ）

A．3 B．2 C． D．

【答案】A

【解析】

 解：过点A作AM⊥BC于点M，交DG于点N，

∵AB＝AC，AD＝AG，

∴AD：AB＝AG：AC，

∵∠BAC＝∠DAG，

∴△ADG∽△ABC，

∴∠ADG＝∠B，

∴DG∥BC，

∵四边形DEFG是正方形，

∴FG⊥DG，

∴FH⊥BC，AN⊥DG，

∵AB＝AC＝10，BC＝12，

∴BM＝BC＝6，

∴AM＝＝＝8，

∵DG∥BC，

∴△ADG∽△ABC，

∴，

∴，

∴AN＝2，

∴MN＝AM﹣AN＝6，

∴FH＝MN﹣GF＝6﹣3＝3，

故选：A．

 3．如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD是△ABC的角平分线，若P，Q分别是AD和AC边上的动点，则PC+PQ的最小值是（  ）

A． B． C． D．

【答案】C

【解析】

 解：如图所示：将△ACD沿AD翻折得到△ADC′，连接DC′，过点C′作C′Q⊥AC．

∵AD是∠CAB的角平分线，
∴△ADC与△ADC′关于AD对称．
∴点C′在AB上．
由翻折的性质可知：AC′＝AC＝3，PC＝PC′．
∴QP＋PC＝QP＋PC′．
由垂线段最短可知：当C′Q⊥AC时，C′Q有最小值．
在Rt△ACB中，AB＝．

∵，

∴，

∴，

∴,

∴，即，

解得：，

∴PC+PQ的最小值是：．

故选：C．

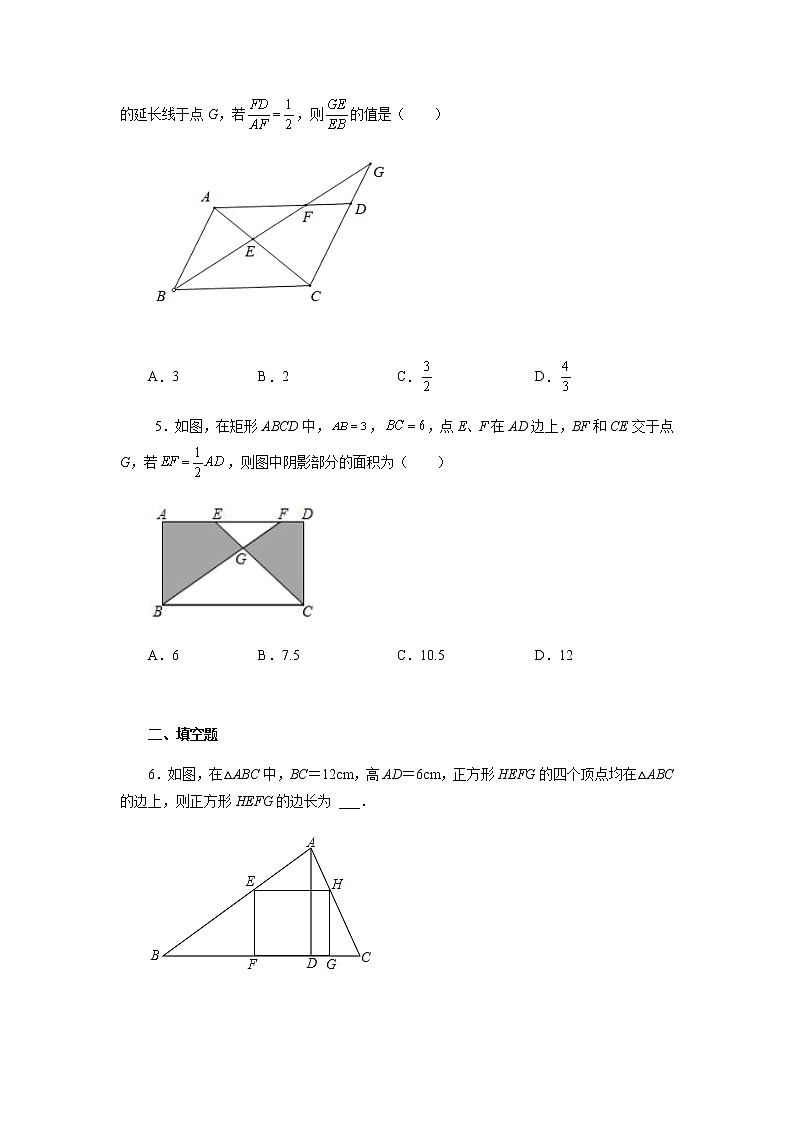
 4．如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E，交AD于点F，交CD的延长线于点G，若，则的值是（　　）

A．3 B．2 C． D．

【答案】C

【解析】

 解：∵四边形ABCD是平行四边形，

∴，，AB=CD，AD=BC，

∴∠ABG=∠G，∠AFB=∠CBG，

∵BG平分∠ABC，

∴∠ABG=∠CBG，

∴∠G=∠CBG，∠ABF=∠AFB=∠DFG=∠G，

∴BC=CG，AF=AB，DF=DG，

∵，

∴设DF=DG=x，则AF=AB=CD=2x，

∴CG=CD+DG=3x，

∵∠ABE=∠G，∠AEB=∠CEG，

∴△ABE∽△CGE，

∴，

故选：C．

 5．如图，在矩形ABCD中，，，点E、F在AD边上，BF和CE交于点G，若，则图中阴影部分的面积为（    ）

A．6 B．7.5 C．10.5 D．12

【答案】C

【解析】

 解：过点G作GN⊥AD于N，延长NG交BC于M，

∵四边形ABCD是矩形，
∴AD=BC，AD∥BC，
∵EF=AD=3，
∴EF=BC，
∵AD∥BC，NG⊥AD，
∴△EFG∽△CBG，GM⊥BC，
∴GN：GM=EF：BC=1：2，
又∵MN=AB=3，
∴GN=1，GM=2，
∴S△BCG=×6×2=6，
∴S△EFG=×3×1=，S矩形ABCD=6×3=18，
∴S阴影=18-6-=10.5．
故选：C．

二、填空题

6．如图，在△ABC中，BC＝12cm，高AD＝6cm，正方形HEFG的四个顶点均在△ABC的边上，则正方形HEFG的边长为 ___．

【答案】4 cm

【解析】

 解：设正方形的边长为xcm，

∴AP＝AD﹣PD＝6﹣x，

∵EH∥BC，

∴△AEH∽△ABC，

∴，

∴＝，

解得：x＝4，

故答案为：4cm

 7．已知：在△ABC中，AB＝5，AC＝4，点D在边AB上，点E在边AC上，AD＝2，当AE＝___时，△ABC和△ADE相似．

【答案】或

【解析】

 解：当时，

∵∠A=∠A，

∴△AED∽△ABC，

此时AE===；

当时，

∵∠A=∠A，

∴△ADE∽△ABC，

此时AE===；

故答案为：或．

 8．如图，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，点D、E分别在BC、AC上，且BD＝CE，设点C关于DE的对称点为F，若DF∥AB，则BD的长为 ___．

【答案】1

【解析】

 解：延长DF交AC于G，

设BD＝CE＝x，

∵∠C＝90°，AB＝5，BC＝3，

∴AC＝4，

∵点C关于DE的对称点为F，

∴EF＝CE＝x，

∵DF∥AB，

∴∠A＝∠EGF，

∴△ABC∽△GEF，

∴，

∴，

∴GE＝，

∴CG＝GE+CE＝，

∵DF∥AB，

∴，

∴，

∴x＝1，

∴BD＝1，

故答案为：1．

 9．如图，在△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，点I为三角形的重心，HI⊥BC于点H，则HI＝______cm．

【答案】2

【解析】

 ：解：BI与AC交于点D．

∵点I为三角形的重心．
∴AD＝DC，DI＝IB．
∵AC＝6cm．
∴DC＝3cm．
∵∠ACB＝90°，HI⊥BC于点H，
∴DC∥HI．
∴△BHI∽△BCD，
∴．即：．
∴HI＝2cm．
故答案为：2．

 10．如图，已知△ABC的中线AD、CE相交于点G，过点E作EF∥BC交AD于点F，那么的值为____．

【答案】

【解析】

 解：∵CE是△ABC的中线，

∴AE＝EB，

∵EF∥BC，

∴＝＝1，

∴＝，

∵△ABC的两条中线AD和CE相交于点G，

∴点G是△ABC的重心，

∴EG＝CG，DG＝AG，

∵EF∥BC，

∴＝＝，即DG＝2FG，

∵AF＝FD，

AF＝3FG，

∴，

故答案为：．

三、解答题

11．如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上．在F点观测A点后，沿FN方向走到M点，观测C点发现∠1＝∠2，测得EF＝15米，FM＝2米，MN＝8米，∠ANE＝45°．

（1）AE＝　 　米，AB＝　 　米；

（2）求矩形场地ABCD的面积．

【答案】

解：（1），，

，

和是等腰直角三角形，

，，

米，米，米，

（米，（米，

（米，（米，

（米；

（2）过作于，过作交于，交于，

，

四边形和四边形是矩形，

，，，

，，

，

，

设，，

，，

，

，

，

，

，

，

，经检验：符合题意；

，

（米，

矩形的面积为：（平方米）.

【解析】

（1）根据已知条件得到和是等腰直角三角形，求得米，米，于是得到米；

（2）过作于，过作交于，交于，根据矩形的性质得到，，，根据相似三角形的性质即可得到结论．

12．已知：中，以为直径的交边于点

（1）求证：点为边的中点；

（2）若，求的长．

【答案】

（1）证明：连结AE，

∵为直径，

∴∠AEB=90°，

∵AE⊥BC，

∴BE=CE=，

点为边的中点；

（2）解：连结DE，

∵∠CDE+∠ADE=180°，∠ABE+∠ADE=180°，

∴∠CDE=∠ABE，

又∵∠DCE=∠BCA，

∴△CDE∽△CBA，

∴，

∵，点为边的中点；

∴CE=，AC=AB=10，

∴，

∴，

∴AD=AC-CD=10-4=6．

【解析】

（1）根据直径所对圆周角是90°可得AE⊥BC，根据等腰三角形三线合一可得BE=CE=即可；

（2）利用平角与四边形对角互补可证得∠CDE=∠ABE，进而可证△CDE∽△CBA，可得，可求即可．

13．如图1，已知在Rt△ABC中，AB＝5cm，BC＝12cm，以BC为边作正方形BCDE，点P从点A出发，沿ABE方向匀速运动，速度为1cm/s；同时，点Q从点C出发，沿CA方向匀速运动，速度为2cm/s，连接PQ．设运动时间为t（s）（0＜t＜6.5），解答下列问题：

（1）当t为何值时，PQ∥BC？

（2）如图2，连接PQ，交BC于点F，是否存在某一时刻t，使△BFP与△QFC相似？

（3）用含t的代数式表示出五边形PEDCQ的面积．

【答案】

解：（1）由题意得，，

∵在Rt△ABC中，AB＝5cm，BC＝12cm，

∴，

∴，

∵，

∴，

∴即，

解得；

（2）∵∠BFP=∠QFC，

∴要使得△BFP与△QFC相似，那么必有另一组对应角相等，

∵∠ABC=∠PBF=90°，∠QCF≠90°，

∴∠FQC=∠FBP=90°，

∴∠FCQ=∠FPB，∠AQP=∠ABC=90°

∴△APQ∽△ACB，

∴即，

解得；

（3）过点Q作QM⊥AB于M，

∴∠AMQ=∠ABC=90°，

又∵∠A=∠A，

∴△AMQ∽△ABC，

∴即，

∴，

∴，

∵，

∴．

【解析】

（1）由题意得，，由勾股定理求出AC=13cm，则，再证明，得到即，由此求解即可；

（2）先根据相似三角形的判定条件得到∠FQC=∠FBP=90°，从而证明△APQ∽△ACB，即，由此求解即可；

（3）过点Q作QM⊥AB于M，则可证△AMQ∽△ABC，得到即，则，再由进行求解即可．

14．如图，在平面直角坐标系中，点O为坐标原点，抛物线与x轴交于A、B两点，交y轴于点C，点D在抛物线上，且点D的坐标为，．

（1）求抛物线的解析式；

（2）P为第一象限抛物线上一点，连接PC、PD，设点P的横坐标为t，的面积为S，求S与t之间的函数关系式；

（3）在（2）的条件下，作轴于点E，点F在线段OC上，，线段BF和CE交于点G，当，求点P的坐标，并求此时的面积．

【答案】

解：（1）∵抛物线，

∴当x=0时，y=8，

∴点C的坐标为(0，8)，OC=8，

∵，

∴，解得：BO=6，

∴点B的坐标为(6，0)，

∴将B(6，0)和D代入得：，

解得：

∴抛物线的解析式为；

（2）如图所示，构造矩形DEFG，

设点P(t，)，

∵四边形DEFG是矩形，D，C(0，8)，

∴E，F，G，

∴，，，，，，

即；

（3）如图所示，过点E作EN⊥BF于点N，过点F作FQ⊥CE于点Q，

∵EN⊥BF，

∴，

∵，

∴，

∴，

∵，

∴，

∵，

∴，

∴，，

∴和都是等腰直角三角形，

由(2)知，，

∴，

∴，

在中，

∴，

，

∴，

∴，

∴，

∴，

∵，

∴++＝，

解得：t=4，

∴，

∴P(4，6)，

∴．

【解析】

（1）首先根据抛物线得出点C的坐标为(0，8)，然后根据可求出点B的坐标为(6，0)，将点B和点D的坐标代入抛物线可求出a和b的值，即可求出抛物线的解析式；

（2）如图所示，构造矩形DEFG，根据题意表示出点P的坐标为(t，)，然后分别表示出点E，F，G的坐标，即可表示出，，和的面积，进而表示出S与t之间的函数关系式；

（3）过点E作EN⊥BF于点N，过点F作FQ⊥CE于点Q，根据题意证明出，，然后根据等腰直角三角形的性质，勾股定理和相似三角形的性质表示出CQ，QG，GE的长度，最后在△OCE中根据勾股定理列出方程求解即可．