安徽省滁州市定远县育才学校2021-2022学年高二分层班下学期期中考试数学（理）试题（含答案）

这是一份安徽省滁州市定远县育才学校2021-2022学年高二分层班下学期期中考试数学（理）试题（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
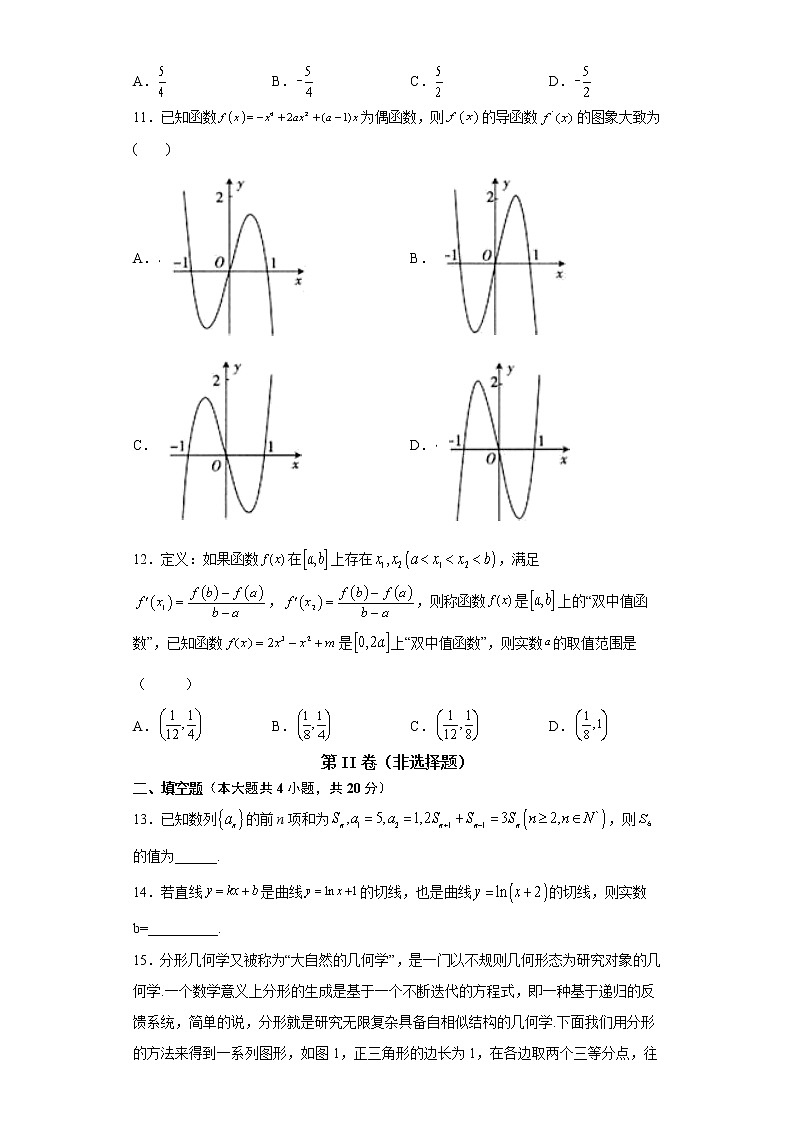
2021-2022学年度第二学期高二分层班期中考试卷理科数学试题第I卷（选择题）一、选择题（本大题共12小题  每小题5分， 满分60分）1．设数列的前n项和为，已知，，则（       ）A．100 B．80 C．75 D．502．若数列满足(，为常数)，则称数列为“调和数列”.已知数列为“调和数列”，且，则（       ）A．15 B．20 C．25 D．303．《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等，问各得几何？”其意思为“已知甲、乙、丙、丁、戊五人分五钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列，”（“钱”是古代一种质量单位），在这个问题中，甲得钱数为（       ）A． B． C． D．4．数列，，，，，中，有序实数对是（       ）A． B．C． D．5．设某厂2020年的产值为1，从2021年起，该厂计划每年的产值比上年增长，则从2021年起到2030年底，该厂这十年的总产值为（       ）A． B．C． D．6．已知函数的图象如图所示，是的导函数，则下列结论正确的是(       )A．B．C．D．7．已知函数，，当时，恒成立，则实数a的取值范围是（       ）A． B． C． D．8．已知函数在上可导，其部分图象如图所示，设，则下列不等式正确的是（        ）A． B．C． D．9．已知为自然对数的底数，曲线在点处的切线与直线垂直，则实数A． B． C． D．10．已知函数的图象在点处的切线与直线垂直，则（       ）A． B． C． D．11．已知函数为偶函数，则的导函数的图象大致为(　　)A． B．C． D．12．定义：如果函数在上存在，满足，，则称函数是上的“双中值函数”，已知函数是上“双中值函数”，则实数的取值范围是（       ）A． B． C． D．第II卷（非选择题）二、填空题（本大题共4小题，共20分）13．已知数列的前n项和为，则的值为______.14．若直线是曲线的切线，也是曲线的切线，则实数b=__________.15．分形几何学又被称为“大自然的几何学”，是一门以不规则几何形态为研究对象的几何学.一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统，简单的说，分形就是研究无限复杂具备自相似结构的几何学.下面我们用分形的方法来得到一系列图形，如图1，正三角形的边长为1，在各边取两个三等分点，往外再作一个正三角形，得到图2中的图形；对图2中的各边作相同的操作，得到图3中的图形；依此类推，我们就得到了以下一系列图形，记第个图形（图1为第一个图形）中的所有外围线段长的和为，则满足的最小正整数的值为______.（参考数据：，）16．对于三次函数，定义：设是函数的导数的导数，若方程有实数解，则称点为函数的“拐点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”请你将这一发现为条件，函数，则它的对称中心为______．三、解答题（本大题共6小题，共70分）17．（10分）已知是公差为d的等差数列，其前n项和是，且，.(1)求数列的通项公式；(2)若，求数列的前n项和.18．（12分）设为数列{}的前n项和，且，．数列{}满足，．(1)求数列{}的通项公式：(2)设数列，求数列{}的前2n项和．19．（12分）已知函数.（1）求曲线y=f(x)在点P(1，-2)处的切线方程；（2）过点P(2，2)作曲线y=f(x)的切线，求此切线的方程.20．（12分）已知函数，．（1）求函数的单调区间；（2）设函数，存在实数，使得不等式成立，求的取值范围．21．（12分）设等差数列的前n项和为，且，，(1)求数列的通项公式：(2)若数列满足，，求数列的前n项和为．22．（12分）已知在函数（）的所有切线中，有且仅有一条切线与直线垂直．（1）求的值和切线的方程；（2）设曲线在任一点处的切线倾斜角为，求的取值范围．
参考答案1．D   2．B  3．C  4．A  5．C  6．B  7．B  8．B 9．C  10．C 11．A  12．B13．   14．.   15．9      16．17．(1)(2)【解析】 (1)由题意，，解得，∴.(2)由，∴.18．(1)；(2).(1)解：由，因为，所以当时，，得：，所以，当时，也适合，因此；(2)解：因为，所以当时，，两式相减得：，由（1）可知：，所以，当时，，也适合上式，故；所以，因此.所以.19．（1）；（2）与.解：（1）由题意可知，则在处的切线斜率，则在点P(1，-2)处的切线方程为：，即切线方程为：.（2）因为，所以设切点为，斜率为则所求切线方程为： ①因为切线过点P(2，2)，所以有解得：或代入①化简可得切线方程为：或.20．（1）答案不唯一，具体见解析；（2）．解：（1）∵，∴（1）当时，∵，∴，，∴单减，∴减区间是．时，，∴单增，∴增区间是．（2）当时，∵，∴，∴的减区间是．（3）当时，∵，∴的减区间是．（4）当时，，∴，∴的增区间是，，，∴的减区间是．（2），因为存在实数，使得不等式成立，∴，∵，，，单减，，，∴单增．∴，．∴，∴，∵，∴．21．(1)(2)(1)解：设等差数列的首项为，公差为，由，，则，解得，所以；(2)解：因为，当时，即，当时，所以，即，当时也成立，所以，所以，，所以，所以.22．（1）（2）或．【解析】（1），由题意知，方程有两个相等的根，∴，∴．此时方程化为，得，解得切点的纵坐标为，∴切线的方程为，即．（2）设曲线上任一点处的切线的斜率为（由题意知存在），则由（1）知，∴由正切函数的单调性可得的取值范围为或．