广东省揭阳市空港区重点达标名校2022年中考一模数学试题含解析

这是一份广东省揭阳市空港区重点达标名校2022年中考一模数学试题含解析，共22页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下折线统计图，则符合这一结果的实验最有可能的是（　　）

A．袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球
B．掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数
C．先后两次掷一枚质地均匀的硬币，两次都出现反面
D．先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过9
2．如图，点E是四边形ABCD的边BC延长线上的一点，则下列条件中不能判定AD∥BE的是（　　）

A． B． C． D．
3．二次函数y＝3（x﹣1）2+2，下列说法正确的是（　　）
A．图象的开口向下
B．图象的顶点坐标是（1，2）
C．当x＞1时，y随x的增大而减小
D．图象与y轴的交点坐标为（0，2）
4．我国古代数学著作《九章算术》卷七“盈不足”中有这样一个问题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”意思是：几个人合伙买一件物品，每人出8元，则余3元；若每人出7元，则少4元，问几人合买？这件物品多少钱？若设有x人合买，这件物品y元，则根据题意列出的二元一次方程组为（　　）
A． B． C． D．
5．若不等式组无解，那么m的取值范围是（　　）
A．m≤2 B．m≥2 C．m＜2 D．m＞2
6．如图，A点是半圆上一个三等分点，B点是弧AN的中点，P点是直径MN上一动点，⊙O的半径为1，则AP＋BP的最小值为

A．1 B． C． D．
7．如图，在矩形ABCD中，AB=2，BC=1．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（　　）

A． B． C． D．
8．如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长度为( )

A． B．4 C． D．
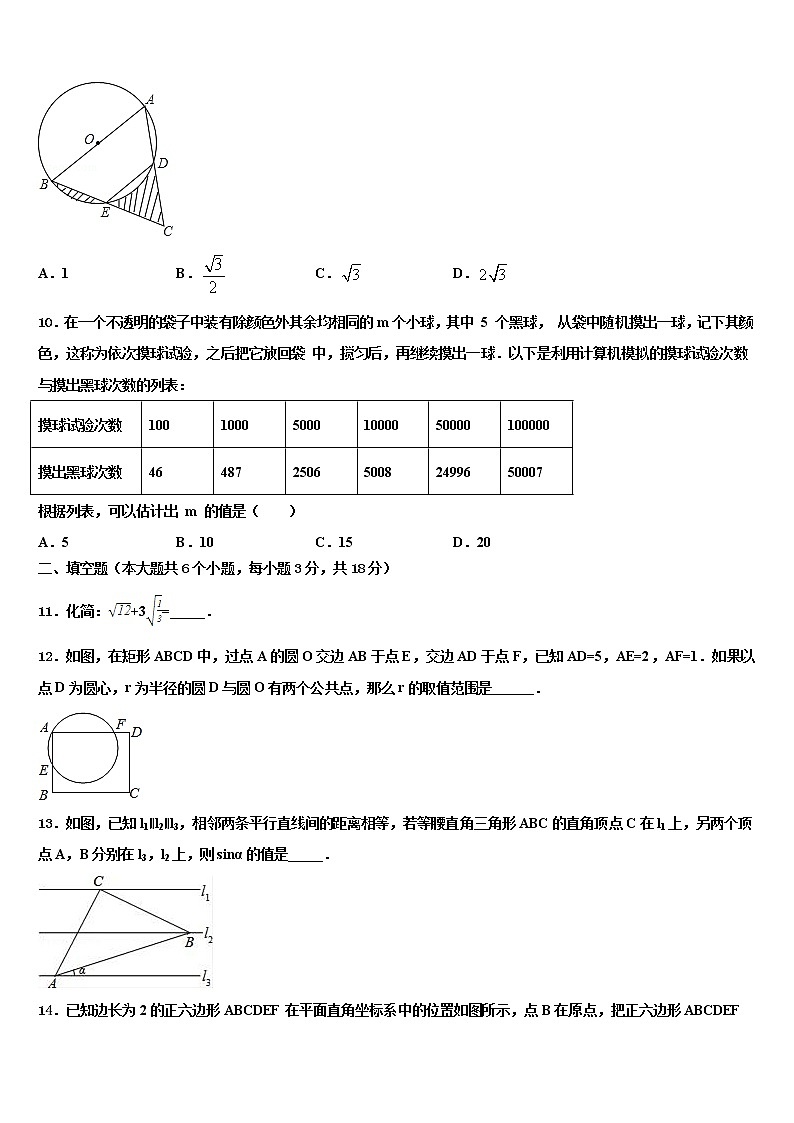
9．如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（ ）

A．1 B． C． D．
10．在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中 5 个黑球， 从袋中随机摸出一球，记下其颜色，这称为依次摸球试验，之后把它放回袋 中，搅匀后，再继续摸出一球．以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：
摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
46
487
2506
5008
24996
50007
根据列表，可以估计出 m 的值是（ ）
A．5 B．10 C．15 D．20
二、填空题（本大题共6个小题，每小题3分，共18分）
11．化简：+3=_____．
12．如图，在矩形ABCD中，过点A的圆O交边AB于点E，交边AD于点F，已知AD=5，AE=2，AF=1．如果以点D为圆心，r为半径的圆D与圆O有两个公共点，那么r的取值范围是______．

13．如图，已知l1∥l2∥l3，相邻两条平行直线间的距离相等，若等腰直角三角形ABC的直角顶点C在l1上，另两个顶点A，B分别在l3，l2上，则sinα的值是_____．

14．已知边长为2的正六边形ABCDEF在平面直角坐标系中的位置如图所示，点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2018次翻转之后，点B的坐标是______．

15．把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB=，则CD=_____．

16．如果等腰三角形的两内角度数相差45°，那么它的顶角度数为_____．
三、解答题（共8题，共72分）
17．（8分）如图，在矩形纸片ABCD中，AB=6，BC=1．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．

（1）求证：△ABG≌△C′DG；
（2）求tan∠ABG的值；
（3）求EF的长．
18．（8分）如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向的B处，求此时轮船所在的B处与灯塔P的距离．（参考数据：≈2.449，结果保留整数）

19．（8分）九（3）班“2017年新年联欢会”中，有一个摸奖游戏，规则如下：有4张纸牌，背面都是喜羊羊头像，正面有2张笑脸、2张哭脸．现将4张纸牌洗匀后背面朝上摆放到桌上，然后让同学去翻纸牌．
（1）现小芳有一次翻牌机会，若正面是笑脸的就获奖，正面是哭脸的不获奖．她从中随机翻开一张纸牌，求小芳获奖的概率．
（2）如果小芳、小明都有翻两张牌的机会．小芳先翻一张，放回后再翻一张；小明同时翻开两张纸牌．他们翻开的两张纸牌中只要出现一张笑脸就获奖．他们获奖的机会相等吗？通过树状图分析说明理由．
20．（8分）武汉二中广雅中学为了进一步改进本校九年级数学教学，提高学生学习数学的兴趣．校教务处在九年级所有班级中，每班随机抽取了6名学生，并对他们的数学学习情况进行了问卷调查：我们从所调查的题目中，特别把学生对数学学习喜欢程度的回答(喜欢程度分为：“非常喜欢”、“ 比较喜欢”、“ 不太喜欢”、“ 很不喜欢”，针对这个题目，问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计．现将统计结果绘制成如下两幅不完整的统计图．

请你根据以上提供的信息，解答下列问题：
（1）补全上面的条形统计图和扇形统计图；
（2）所抽取学生对数学学习喜欢程度的众数是　　，图②中所在扇形对应的圆心角是　　；
（3）若该校九年级共有960名学生，请你估算该年级学生中对数学学习“不太喜欢”的有多少人？
21．（8分）如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G，K在同一直线上）．（cos80°≈0.17，sin80°≈0.98，≈1.414）

（1）此时小强头部E点与地面DK相距多少？
（2）小强希望他的头部E恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少？
22．（10分）计算：﹣22+（π﹣2018）0﹣2sin60°+|1﹣|
23．（12分）计算：（﹣1）2018﹣2+|1﹣|+3tan30°．
24．近年来，新能源汽车以其舒适环保、节能经济的优势受到热捧，随之而来的就是新能汽车销量的急速增加，当前市场上新能漂汽车从动力上分纯电动和混合动力两种，从用途上又分为乘用式和商用式两种，据中国汽车工业协会提供的信息，2017年全年新能源乘用车的累计销量为57.9万辆，其中，纯电动乘用车销量为46.8万辆，混合动力乘用车销量为11.1万辆； 2017年全年新能源商用车的累计销量为19.8万辆，其中，纯电动商用车销量为18.4万辆，混合动力商用车销量为1.4万辆，请根据以上材料解答下列问题：
（1）请用统计表表示我国2017年新能源汽车各类车型销量情况；
（2）小颖根据上述信息，计算出2017年我国新能源各类车型总销量为77.7万辆，并绘制了“2017年我国新能源汽车四类车型销量比例”的扇形统计图，如图1，请你将该图补充完整（其中的百分数精确到0.1%）；

（3）2017年我国新能源乘用车销量最高的十个城市排名情况如图2，请根据图2中信息写出这些城市新能源乘用车销售情况的特点（写出一条即可）；
（4）数据显示，2018年1～3月的新能源乘用车总销量排行榜上位居前四的厂家是比亚迪、北汽、上汽、江准，参加社会实践的大学生小王想对其中两个厂家进行深入调研，他将四个完全相同的乒乓球进行编号（用“1，2，3，4”依次对应上述四个厂家），并将乒乓球放入不透明的袋子中搅匀，从中一次拿出两个乒乓球，根据乒乓球上的编号决定要调研的厂家．求小王恰好调研“比亚迪”和“江淮”这两个厂家的概率．



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、D
【解析】
根据统计图可知，试验结果在0.33附近波动，即其概率P≈0.33，计算四个选项的概率，约为0.33者即为正确答案．
【详解】
解: 根据统计图可知，试验结果在0.33附近波动，即其概率P≈0.33，
A、袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球的概率为，不符合题意；
B、掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数的概率为，不符合题意；
C、先后两次掷一枚质地均匀的硬币，两次都出现反面的概率为，不符合题意；
D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过9的概率为，符合题意，
故选D．
【点睛】
本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：概率=所求情况数与总情况数之比．
2、A
【解析】
利用平行线的判定方法判断即可得到结果．
【详解】
∵∠1=∠2，
∴AB∥CD，选项A符合题意；
∵∠3=∠4，
∴AD∥BC，选项B不合题意；
∵∠D=∠5，
∴AD∥BC，选项C不合题意；
∵∠B+∠BAD=180°，
∴AD∥BC，选项D不合题意，
故选A．
【点睛】
此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
3、B
【解析】
由抛物线解析式可求得其开口方向、顶点坐标、最值及增减性，则可判断四个选项，可求得答案．
【详解】
解：A、因为a＝3＞0，所以开口向上，错误；
B、顶点坐标是（1，2），正确；
C、当x＞1时，y随x增大而增大，错误；
D、图象与y轴的交点坐标为（0，5），错误；
故选：B．
【点睛】
考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y＝a（x﹣h）2+k中，对称轴为x＝h，顶点坐标为（h，k）．
4、D
【解析】
根据题意可以找出题目中的等量关系，列出相应的方程组，从而可以解答本题．
【详解】
由题意可得：，
故选D．
【点睛】
本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．
5、A
【解析】
先求出每个不等式的解集，再根据不等式组解集的求法和不等式组无解的条件，即可得到m的取值范围．
【详解】

由①得，x＜m，
由②得，x＞1，
又因为不等式组无解，
所以m≤1．
故选A．
【点睛】
此题的实质是考查不等式组的求法，求不等式组的解集，要根据以下原则：同大取较大，同小较小，小大大小中间找，大大小小解不了．
6、C
【解析】
作点A关于MN的对称点A′,连接A′B，交MN于点P，则PA+PB最小，

连接OA′,AA′.
∵点A与A′关于MN对称，点A是半圆上的一个三等分点，
∴∠A′ON=∠AON=60°,PA=PA′，
∵点B是弧AN∧的中点，
∴∠BON=30 °，
∴∠A′OB=∠A′ON+∠BON=90°，
又∵OA=OA′=1，
∴A′B=
∴PA+PB=PA′+PB=A′B=
故选：C.
7、B
【解析】
根据S△ABE=S矩形ABCD=1=•AE•BF，先求出AE，再求出BF即可．
【详解】
如图，连接BE．

∵四边形ABCD是矩形，
∴AB=CD=2，BC=AD=1，∠D=90°，
在Rt△ADE中，AE===，
∵S△ABE=S矩形ABCD=1=•AE•BF，
∴BF=．
故选：B．
【点睛】
本题考查矩形的性质、勾股定理、三角形的面积公式等知识，解题的关键是灵活运用所学知识解决问题，学会用面积法解决有关线段问题，属于中考常考题型．
8、B
【解析】
求出AD＝BD，根据∠FBD＋∠C＝90°，∠CAD＋∠C＝90°，推出∠FBD＝∠CAD，根据ASA证△FBD≌△CAD，推出CD＝DF即可．
【详解】
解：∵AD⊥BC，BE⊥AC，
∴∠ADB=∠AEB=∠ADC=90°，
∴∠EAF+∠AFE=90°，∠FBD+∠BFD=90°，
∵∠AFE=∠BFD，
∴∠EAF=∠FBD，
∵∠ADB=90°，∠ABC=45°，
∴∠BAD=45°=∠ABC，
∴AD=BD，
在△ADC和△BDF中 ，
∴△ADC≌△BDF，
∴DF=CD=4，
故选：B．
【点睛】
此题主要考查了全等三角形的判定，关键是找出能使三角形全等的条件．
9、C
【解析】
连接AE，OD，OE．

∵AB是直径， ∴∠AEB=90°．
又∵∠BED=120°，∴∠AED=30°．∴∠AOD=2∠AED=60°．
∵OA=OD．∴△AOD是等边三角形．∴∠A=60°．
又∵点E为BC的中点，∠AED=90°，∴AB=AC．
∴△ABC是等边三角形，
∴△EDC是等边三角形，且边长是△ABC边长的一半2，高是．
∴∠BOE=∠EOD=60°，∴和弦BE围成的部分的面积=和弦DE围成的部分的面积．
∴阴影部分的面积=．故选C．
10、B
【解析】
由概率公式可知摸出黑球的概率为，分析表格数据可知的值总是在0.5左右，据此可求解m值.
【详解】
解：分析表格数据可知的值总是在0.5左右，则由题意可得，解得m=10,
故选择B.
【点睛】
本题考查了概率公式的应用.

二、填空题（本大题共6个小题，每小题3分，共18分）
11、
【解析】
试题分析：先进行二次根式的化简，然后合并，可得原式=2+=3．
12、
【解析】
因为以点D为圆心，r为半径的圆D与圆O有两个公共点，则圆D与圆O相交，圆心距满足关系式：|R-r|