人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理优质课件ppt

课题名

空间向量基本定理

课型

新授课

教学目标

1.能进行空间向量的降维分解；

2.掌握空间向量基本定理，掌握基底的概念；

3.以空间向量基本定理作为工具解决几何中的有关问题.

教学重难点

重点：空间向量基本定理；

难点：利用空间向量基本定理作为工具解决几何中的有关问题.

为了更好地突破难点，在素养篇里配备了问题1、问题2、问题3，落实核心素养一级目标和二级目标；另外，在思维篇里配备了问题1、问题2，用基底表示目标向量时，引入了参数，使学生从根本上理解定理的本质，强化基本定理的应用.

同时，通过从一级目标的落实到三级目标的达成，让学生切实掌握以基底为桥梁解决几何问题的方法.

教学环节

教学过程

课堂导入

平面向量基本定理

    如果a,b是平面内的两个不共线向量，那么对于这一平面内的任一向量p，有且只有一对实数x、y，使p=xa+yb .

课

程

学

习

一、空间向量的分解

如图，将空间不共面的三个向量a,b,c以及空间任意向量p平移至

共起点O；

过点P作c的平行线，交a,b所在平面于点Q，则有+=p ;

根据平面向量基本定理，存在唯一实数对(x,y),使得：

                     =xa+yb;

因为∥c，所以存在唯一实数z，使得：=zc;

从而：=xa+yb+zc .

二、空间向量基本定理

    如果三个向量a,b,c不共面，那么对任意一个空间向量p，存在唯一的有序实数对(x,y,z)，使得：p=xa+yb+zc .

其中，{a,b,c}叫做空间的一个基底，而a,b,c都叫做基向量.

空间任意三个不共面的向量都可以构成空间的一个基底.

特别地，如果空间的一个基底中的三个基向量两两垂直，且长度都为1，那么这个基底叫做单位正交基底，常用{i,j,k}表示.

把空间任意一个向量a分解成xi, yj, zk，叫做把空间向量进行正交分解.

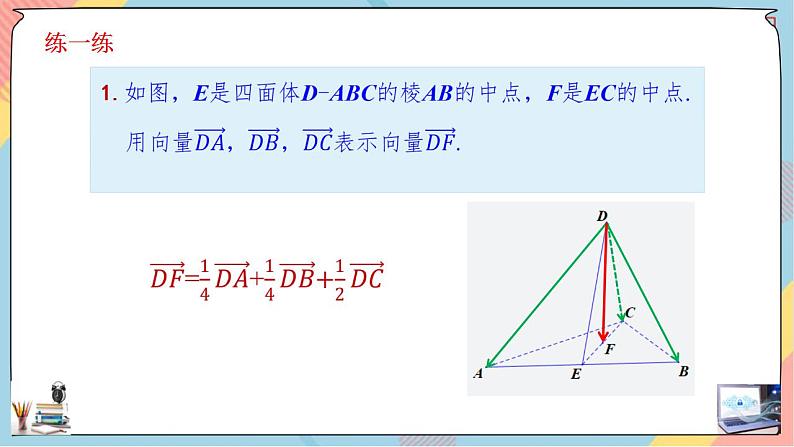
练习：

1.如图，E是四面体D-ABC的棱AB的中点，F是EC的中点. 

   用向量，，表示向量.

2.已知{a,b,c}是空间一个基底，则以下向量中能与a，a-b

      构成基底的是(   )

     A、b        B、c       C、b-a        D、b+a

三、核心素养提升

 1.如图，平行六面体ABCD-A’B’C’D’的底面ABCD是菱形，∠C’CB=∠C’CD,求证：B’D’⊥CA’ .   

2.如图，在棱长为1的正方体ABCD-A'B'C'D'中，E、F，G分别为DD',BD,DC的中点.，且DG=3GC.求EF与C'G所成角的余弦值.

3.如图，在正三棱台ABC-A'B'C'中，AB=2AA'=2A'B'=4, 

  E、F分别为CC',A'B'的中点，求线段EF的长.                                 

四、思维方法训练

  问题1

1.如图，已知平行六面体ABCD-A'B'C'D'的体积为3，点P

    是六面体AC'内部(含表面)一动点,满足条件：

    则点P轨迹的体积为           .

问题2

2.如图，正方体ABCD-A'B'C'D'中，M、N、E分别为棱AB、DD’、BC的中点;在对角线A'C'上是否存在一点F，使得MN与EF垂直？若存在，试确定点F的位置；若不存在，说明理由.

课堂

小结

一、本节课新知识回顾（由师生共同完成）

二、本节课核心素养方法回顾

三、本节课用到的数学思想方法回顾

板书设计

教学反思