第十七章 勾股定理选择填空题专项练 2021-2022学年初中数学八年级下册期末复习（有答案）

这是一份第十七章 勾股定理选择填空题专项练 2021-2022学年初中数学八年级下册期末复习（有答案），共27页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。

第十七章 勾股定理选择填空题专项练
一、单选题
1．由于台风的影响，一棵树在离地面6m处折断，树顶落在离树干底部8m处，则这棵树在折断前（不包括树根）长度是（       ）

A．8m B．10m C．16m D．18m
2．已知中，，BD是AC边上的高线，，那么BD等于（       ）

A．2 B．4 C．6 D．8
3．如图，正方形A、B、C的边长分别为直角三角形的三边长，若正方形A、B的边长分别为3和5，则正方形C的面积为(     )

A．4 B．15 C．16 D．18
4．已知，Rt△ABC中，∠A＝90°，AB＝4，BC＝5，AC边的长为（　　）
A．3 B． C．3或 D．
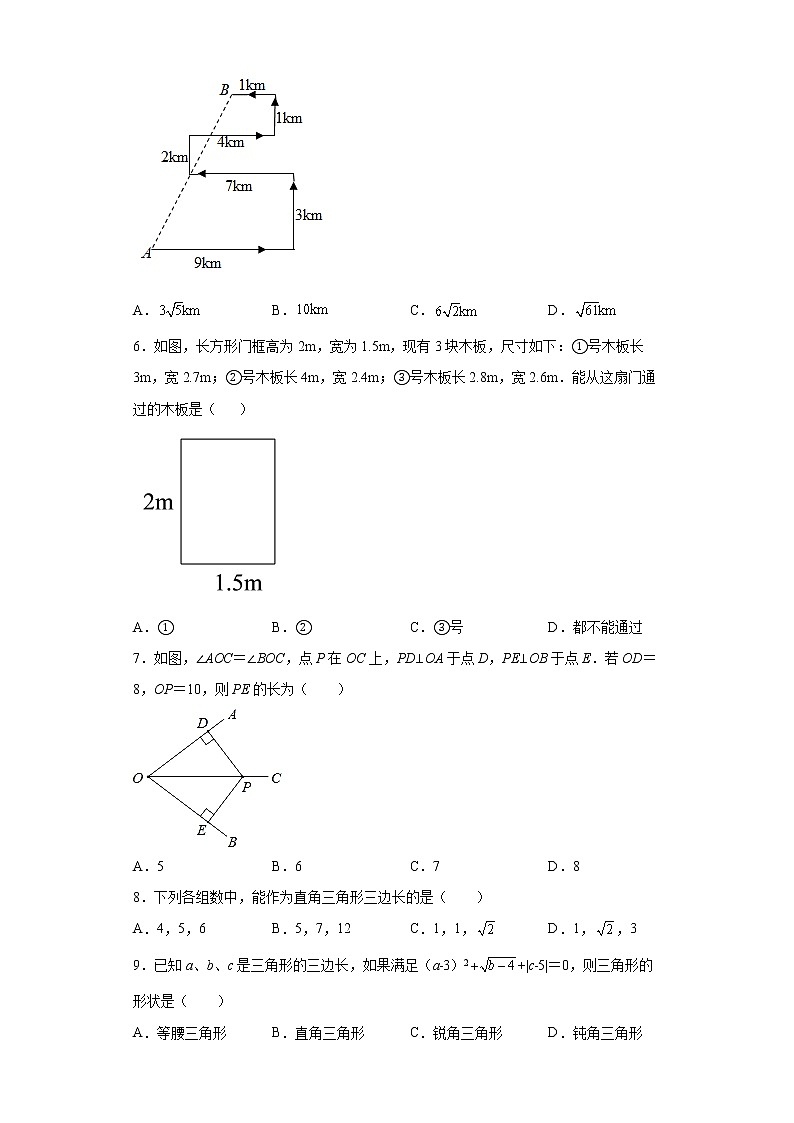
5．国庆假期间，妍妍与同学去玩寻宝游戏，按照藏宝图，她从门口A处出发先往东走9km，又往北走3km，遇到障碍后又往西走7km，再向北走2km，再往东走了4km，发现走错了之后又往北走1km，最后再往西走了1km就找到了宝藏，则门口A到藏宝点B的直线距离是（       ）

A． B． C． D．
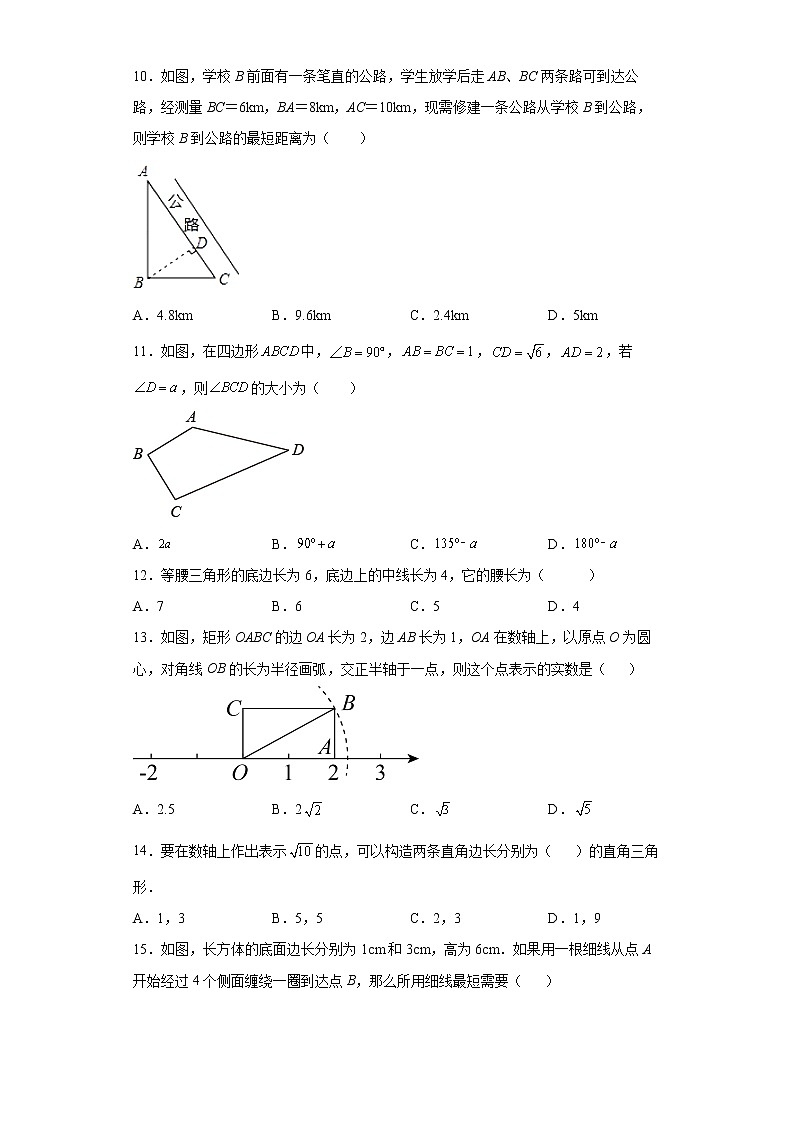
6．如图，长方形门框高为2m，宽为1.5m，现有3块木板，尺寸如下：①号木板长3m，宽2.7m；②号木板长4m，宽2.4m；③号木板长2.8m，宽2.6m．能从这扇门通过的木板是（       ）

A．① B．② C．③号 D．都不能通过
7．如图，∠AOC＝∠BOC，点P在OC上，PD⊥OA于点D，PE⊥OB于点E．若OD＝8，OP＝10，则PE的长为（　　）

A．5 B．6 C．7 D．8
8．下列各组数中，能作为直角三角形三边长的是（　　）
A．4，5，6 B．5，7，12 C．1，1， D．1，，3
9．已知a、b、c是三角形的三边长，如果满足（a﹣3）2+|c﹣5|＝0，则三角形的形状是（　　）
A．等腰三角形 B．直角三角形 C．锐角三角形 D．钝角三角形
10．如图，学校B前面有一条笔直的公路，学生放学后走AB、BC两条路可到达公路，经测量BC＝6km，BA＝8km，AC＝10km，现需修建一条公路从学校B到公路，则学校B到公路的最短距离为（　　）

A．4.8km B．9.6km C．2.4km D．5km
11．如图，在四边形中，，，，，若，则的大小为（　　）

A． B． C． D．
12．等腰三角形的底边长为6，底边上的中线长为4，它的腰长为（　　　）
A．7 B．6 C．5 D．4
13．如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（       ）

A．2.5 B．2 C． D．
14．要在数轴上作出表示的点，可以构造两条直角边长分别为（       ）的直角三角形．
A．1，3 B．5，5 C．2，3 D．1，9
15．如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要（       ）

A．8 cm B．10 cm C．12 cm D．15 cm
16．如图，在边长为1个单位长度的小正方形组成的网格中，点、都是格点，则线段的长度为（　　）

A．5 B．6 C．7 D．25
17．△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（　　）
A．42 B．32 C．42或32 D．14或4
18．如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝2．以点B为圆心，BC为半径画弧交AB于点D，再以点A为圆心，AD为半径画弧交AC于点E．则CE的长等于（　　）

A．﹣1 B． C． D．1
19．已知直角三角形的两边长分别为6和8，则斜边长为（       ）
A．8 B．10 C．8或10 D．10或
20．如图，有一个水池，水面是一个边长为14尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．则水的深度是（       ）

A．15尺 B．24尺 C．25尺 D．28尺
21．如图，是一段楼梯，高BC是1.5m，斜边AC是2.5m，如果在楼梯上铺地毯，那么至少需要地毯（　　）

A．2.5m B．3m C．3.5m D．4m
22．如图，一只蜘蛛在一块长方体木块的一个顶点A处，一只苍蝇在这个长方体的对角顶点G处，若AB＝3cm，BC＝5cm，BF＝6cm，则最短的爬行距离是（　　）

A．10 B．14 C． D．
23．若将三条高线长度分别为x，y，z的三角形记为（x，y，z），则以下三角形（6，8，10），（8，15，17），（12，15，20），（20，21，29）中，直角三角形的个数为（       ）．
A．1个 B．2个 C．3个 D．4个
24．如图，每个小正方形的边长都相等，A，B，C是小正方形的顶点，则的度数为（     ）

A． B． C． D．
25．如图，一个长为10米的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8米，如果梯子的顶端下滑1米，那么梯子的底端的滑动距离（　　）

A．等于1米 B．大于1米 C．小于1米 D．不能确定
26．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为　　

A．9 B．6 C．4 D．3
27．如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（       ）

A．8 B．9 C．10 D．11
28．如图，在矩形纸片ABCD中，AD＝9，AB＝3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为（       ）

A．3 B． C． D．9
二、填空题
29．三角形的两边长分别为和，要使这个三角形是直角三角形，则第三条边长是______．
30．如图，该图形是由直角三角形和正方形构成，其中最大正方形的边长为5，则正方形、、、的面积之和为______．

31．在三角形ABC中，∠C=90°，AB=7，BC=5，则AC的长为__________________.
32．填空：
（1）如图，圆柱的侧面展开图是_____，点B的位置应在长方形的边CD的_____，点A到点B的最短距离为线段_____的长度．
（2）AB＝_____．

33．（1）已知甲、乙两人在同一地点出发，甲往东走了4 km，乙往南走了3 km，这时甲、乙两人相距_____km．
（2）如图是某地的长方形大理石广场示意图，如果小王从A角走到C角，至少走_____米．

（3）如图：有一个圆柱，底面圆的直径AB＝ ，高BC＝12，P为BC的中点，蚂蚁从A点爬到P点的最短距离是_____．

34．已知a、b、c是△ABC的三边长且c=5，a、b满足关系式，则△ABC的形状为_____三角形．
35．如图，在△ABC中，AC＝4，∠A＝60°，∠B＝45°，BC边的垂直平分线DE交AB于点D，连接CD，则AB的长为_________________．

36．课间，小明拿着老师的等腰直角三角板玩，不小心掉到两墙之间（如图），，，从三角板的刻度可知，小明很快就知道了砌墙砖块的厚度为______ cm（每块砖的厚度相等）．

37．如图，在平面直角坐标系中，已知点A（0，8），B（﹣6，0），连接AB．将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则点C的坐标为 ___．

38．轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则B处与灯塔A的距离是__________海里．

39．如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是 _____秒．

40．“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=0.5千米，则该沙田的面积为________________平方千米．

1．C
【详解】
解：由题意得BC＝8m，AC＝6m，
在直角三角形ABC中，根据勾股定理得：AB＝＝10米．
所以大树的高度是10＋6＝16米．
故选：C．
．
2．C
【详解】
解：∵AB=AC=10，DC=2，
∴AD= AC-DC=8，
∴.
故选：C．
3．C
【详解】
∵正方形A、B的边长分别为3和5，
∴正方形C的边长为=，
所以正方形C的面积为42=16，
4．A
【详解】
解：如图所示，

∵∠A＝90°，AB＝4，BC＝5，
∴．
5．D
【详解】
解：如图，过点作于点，

则，，
在中，，
6．B
【详解】
如图，连接

四边形是长方形


所以此门通过的木板的宽最大为2.5m
所以木板的长和宽中必须有一个数据小于2.5米．所以选②号木板．
7．B
【详解】
解：∵PD⊥OA，
∴∠PDO＝90°，
∵OD＝8，OP＝10，
∴PD＝＝6，
∵∠AOC＝∠BOC，点P在OC上，PD⊥OA，PE⊥OB，
∴PE＝PD＝6．
故选：B．
8．C
【详解】
，故A不符合题意；
，故B不符合题意；
，故C符合题意；
，故D不符合题意；
9．B
【详解】
解：∵（a﹣3）2+|c﹣5|＝0，
∴ ，
解得： ，
∵ ，
∴该三角形的形状是直角三角形．
10．A
【详解】
解：过B作BD⊥AC，垂足为D，
∵62＋82＝102，
∴BC2＋AB2＝AC2，
∴∠ABC＝90°，
S△ACB＝AB•CB＝AC•BD，
×6×8＝×10×DB，
解得：BD＝4.8，
∴学校B到公路的最短距离为4.8km，
11．C
【详解】
连接AC，

∵AB=BC=1，∠B=90°
∴AC=，
又∵AD=2，DC=，
∴()2=22+()2，
即CD2=AD2+AC2，
∴∠DAC=90°，
∵，
∴∠ACD=90°-α，
∵AB=BC，
∴∠BAC=∠BCA=45°，
∴∠BCD=90°-α+45°=135°-α；
12．C
【详解】
解：如解图，
∵等腰三角形中，，是上的中线，
∴，同时是上的高线，
∴．

13．D
【详解】
解：四边形OABC是矩形，
，
在中，由勾股定理可知：，
，
弧长为，故在数轴上表示的数为，
14．A
【详解】
解：由勾股定理可得：
A、斜边长为，故符合题意；
B、斜边长为，故不符合题意；
C、斜边长为，故不符合题意；
D、斜边长为，故不符合题意；
15．B
【详解】
解：将长方体沿着边侧面展开，并连接，如下图所示：

由题意及图可知：，，
两点之间，线段最短，故的长即是细线最短的长度，
中，由勾股定理可知：，
故所用细线最短需要．
16．A
【详解】
解：如图所示：

．
17．C
【详解】
解：情况一：如下图，△ABC是锐角三角形，

∵AD是高，
∴AD⊥BC，
∵AB=15，AD=12，
∴在Rt△ABD中，BD=9，
∵AC=13，AD=12，
∴在Rt△ACD中，DC=5，
∴△ABC的周长为：15+13+9+5=42；
情况二：如下图，△ABC是钝角三角形，

在Rt△ADC中，AD=12，AC=13，
∴DC=5，
在Rt△ABD中，AD=12，AB=15，
∴DB=9，
∴BC=BD-CD=9-5=4，
∴△ABC的周长为：15+13+4=32；
∴△ABC的周长为：42或32．
18．A
【详解】
解：，
，
，
，
，
19．C
【详解】
解：当8为直角边时，斜边，
当8为斜边时，另一条直角边，
20．B
【详解】
解：依题意画出图形，设芦苇长AB=AB′=x尺，则水深AC=（x-1）尺，因为B'E=14尺，所以B'C=7尺
在Rt△AB'C中，∵CB′2+AC2=AB′2
∴72+（x-1）2=x2，
解得x=25，
∴水深为：25-1=24尺，
故选B．

21．C
【详解】
解：由勾股定理得： AB=
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和
所以地毯的长度至少是1.5+2=3.5（m）
22．A
【详解】
把长方体展开有三种情况：
当蜘蛛从A 出发到EF上再到G时，如下图所示

，
，
，
在中，；
当蜘蛛从A 出发到BF上再到G时，如下图所示

，，
，
，
，
在中，，
当蜘蛛从A 出发到EH上再到G时，如下图所示

， ，
∴AF=9cm，
在中，，
．
23．A
【详解】
解：∵直角三角形斜边上的高一定会比直角边其中一边短，（原理可以参考三角形面积求法）
∴假设三角形（6，8，10），是直角三角形，
∴10一定是一条直角边，假设6是另一条直角边，
∴斜边=6×10÷8=7.5＜10，不成立，
同理得到8是另一条直角边为，斜边=10×8÷6= ，
∵ ，
∴此时不是直角三角形；
假设三角形（8，15，17）是直角三角形
∴17一定是一条直角边，假设8是另一条直角边，
∴斜边=17×8÷15=，不成立，
同理得到15是另一条直角边为，斜边=17×15÷8= ，
∵ ，
∴此时不是直角三角形；
假设三角形（12，15，20）是直角三角形
∴20一定是一条直角边，假设12是另一条直角边，
∴斜边=10×12÷15=，不成立，
同理得到15是另一条直角边为，斜边=20×15÷12=25 ，
∵ ，
∴此时是直角三角形；
假设三角形（20，21，29）是直角三角形
∴29一定是一条直角边，假设20是另一条直角边，
∴斜边=29×20÷21=，不成立，
同理得到21是另一条直角边为，斜边=29×21÷20= ，
∵ ，
∴此时不是直角三角形；
24．A
【详解】
解：如图，连结AC，

由题意可得：

∴AC=BC，，
∴△ABC是等腰直角三角形，
∴∠ABC=∠BAC=45°，
25．B
【详解】
如图，
AC＝EF＝10米，AB＝8米，AE＝1米，求CF；
∵∠B＝90°，由勾股定理得，BC＝6米，
又∵AE＝1米，BE＝7米，EF＝10米，由勾股定理得，BF＝米，
∵＞，即＞7，
∴﹣6＞1，
故选B．

26．D
【详解】
解：由题意可知：中间小正方形的边长为：，
每一个直角三角形的面积为：，
，
，
或（舍去），
27．C
【详解】
解：如图，
∵a、b、c都是正方形，
∴AC=CD，∠ACD=∠ABC=∠DEC=90°，
∴∠ACB+∠DCE=∠ACB+∠BAC=90°，即∠BAC=∠DCE，
在△ABC和△CED中，，
∴△ACB≌△CDE（AAS），
∴AB=CE，BC=DE；
在Rt△ABC中，由勾股定理得：AC2=AB2+BC2=AB2+DE2，
即Sb=Sa+Sc=1+9=10，
∴b的面积为10，

28．C
【详解】
过点F做交AD于点H．

∵四边形是四边形沿EF折叠所得，
∴ED=BE，CF=，
∵ED=BE，DE=AD-AE=9-AE
∴BE=9-AE
∵，AB=3，BE=9-AE
∴
∴AE=4
∴DE=5
∴
∴，,
∴
∴BF=5，EH=1
∵，HF=3，EH=1
∴
29．或##或
【详解】
解：∵三角形的两边长分别为1cm和2cm，
∴可设第三边为x cm，
∵此三角形是直角三角形，
∴当x是斜边时，，解得x=；
当x是直角边时，，解得x=．
故答案为：或
30．
【详解】
解：如图，

最大正方形的边长为5，
，
根据勾股定理的几何意义得：，，，
．
故答案为：25．
31．．
解：根据勾股定理列式计算即可得解：

∵∠C=90°，AB=7，BC=5，
∴．
故答案为：．
32．     长方形     中点处     AB##BA     ##
【详解】
解：（1）如图，圆柱的侧面展开图是长方形，点B的位置应在长方形的边CD的中点处，点A到点B的最短距离为线段AB的长度．
故答案为：长方形；中点处；AB；
（2）由勾股定理得： ．
故答案为：．
33．     5     50     10
【详解】
解：（1）如图，


∵∠AOB=90°，OA=4km，OB=3km，
∴AB==5km．
故答案为：5；
（2）如图连接AC，

∴四边形ABCD是矩形，
∴∠B=90°，
在Rt△ABC中，∵∠B=90°，AB=30米，BC=40米，
∴AC==50(米)．
根据两点之间线段最短可知，小王从A角走到C角，至少走50米，
故答案为：50；
（3）解：已知如图：

∵圆柱底面直径AB=，高BC=12，P为BC的中点，
∴圆柱底面圆的半径是，BP=6，
∴AB=×2וπ=8，
在Rt△ABP中，
AP==10，
∴蚂蚁从A点爬到P点的最短距离为10．
故答案为：10．
34．直角
【详解】
解：由得：，，
解得：，，
∵，
∴，
∴△ABC的形状为直角三角形，且∠B=90°，
故答案为：直角．
35．2＋2
【详解】
解：∵DE是BC的垂直平分线，
∴DB＝DC，
∴∠DCB＝∠B＝45°，
∴∠ADC＝∠DCB＋∠B＝90°，
∵∠A＝60°，
∴∠ACD＝30°，
∴AD＝AC＝2，
由勾股定理得：DC＝＝＝2，
∴DB＝DC＝2，
∴AB＝AD＋DB＝2＋2，
故答案为：2＋2．
36．
【详解】
,









设砌墙砖块的厚度为 cm，
则，，
在中，


解得（负值舍去）
砌墙砖块的厚度为
故答案为：．
37．
【详解】
解：点A（0，8），B（﹣6，0），
，
在中，
，
将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，

设则
在中，，
，
解得，
点C的坐标为
故答案为：．
38．
【详解】
解：∵灯塔A在B处南偏东方向上，C处在B处南偏东方向上，
∴，B处在C处的北偏西方向上．
∴．
∴．
∴．
∴AC=BC．
∵轮船从B处以每小时50海里的速度航行半小时到达C处，
∴海里．
∴AC=25海里．
∴海里．
故答案为：．
39．18
【详解】

如图，过点A作AC⊥ON于N，
∵∠MON＝30°，OA＝80米，
∴AC＝40米，
当第一台拖拉机到B点时对学校产生噪音影响，此时AB＝50米，
由勾股定理得：（米），
第一台拖拉机到D点时噪音消失，
所以CD＝30米，
由于两台拖拉机相距30米，则第一台到D点时第二台在C点，还须前行30米后才对学校没有噪音影响．
所以影响时间应是：90÷5＝18（秒）．
答：这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒．
故答案为：18．
40．7.5
【详解】
解：∵52+122=132，
∴三条边长分别为5里，12里，13里，构成了直角三角形，
∴这块沙田面积为：×5×500×12×500=7500000（平方米）=7.5（平方千米）．
故答案为7.5．