江西省上饶县联考2022年中考数学押题试卷含解析

这是一份江西省上饶县联考2022年中考数学押题试卷含解析，共24页。
2021-2022中考数学模拟试卷注意事项：1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。 一、选择题（共10小题，每小题3分，共30分）1．下列各数中是有理数的是（　　）A．π B．0 C． D．2．下列各数中，为无理数的是（　　）A． B． C． D．3．△ABC的三条边长分别是5，13，12，则其外接圆半径和内切圆半径分别是（　　）A．13，5 B．6.5，3 C．5，2 D．6.5，24．从1、2、3、4、5、6这六个数中随机取出一个数，取出的数是3的倍数的概率是（　　）A． B． C． D．5．去年二月份，某房地产商将房价提高40%，在中央“房子是用来住的，不是用来炒的”指示下达后，立即降价30%．设降价后房价为x，则去年二月份之前房价为（　　）A．（1+40%）×30%x B．（1+40%）（1﹣30%）xC． D．6．如图，不等式组的解集在数轴上表示正确的是（　　）A． B．C． D．7．在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（　　）A．y1 B．y2 C．y3 D．y48．如图所示是小孔成像原理的示意图，根据图中所标注的尺寸，求出这支蜡烛在暗盒中所成像的长（  ）A． B． C． D．9．一个多边形的每个内角均为120°，则这个多边形是（   ）A．四边形 B．五边形 C．六边形 D．七边形10．若在同一直角坐标系中，正比例函数y＝k1x与反比例函数y＝的图象无交点，则有(　　)A．k1＋k2＞0 B．k1＋k2＜0 C．k1k2＞0 D．k1k2＜0二、填空题（本大题共6个小题，每小题3分，共18分）11．如果关于x的方程（m为常数）有两个相等实数根，那么m＝______．12．如图，矩形OABC的两边落在坐标轴上，反比例函数y=的图象在第一象限的分支过AB的中点D交OB于点E，连接EC，若△OEC的面积为12，则k=_____．13．如图，在△ABC中，∠ACB=90°，AB=8，AB的垂直平分线MN交AC于D，连接DB，若tan∠CBD=，则BD=_____．14．函数中，自变量的取值范围是_____．15．PA、PB分别切⊙O于点A、B，∠PAB=60°，点C在⊙O上，则∠ACB的度数为_____．16．如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．（1）AB的长等于____；（2）在△ABC的内部有一点P，满足S△PABS△PBCS△PCA =1：2：3，请在如图所示的网格中，用无刻度的直尺，画出点P，并简要说明点P的位置是如何找到的（不要求证明）_______三、解答题（共8题，共72分）17．（8分） “千年古都，大美西安”．某校数学兴趣小组就“最想去的西安旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，（景点对应的名称分别是：A：大雁塔  B：兵马俑 C：陕西历史博物馆 D：秦岭野生动物园 E：曲江海洋馆）．下面是根据调查结果进行数据整理后绘制出的不完整的统计图：请根据图中提供的信息，解答下列问题：（1）求被调查的学生总人数；（2）补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；（3）若该校共有800名学生，请估计“最想去景点B”的学生人数．18．（8分）一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外都相同，其中红球有1个，若从中随机摸出一个球，这个球是白球的概率为．求袋子中白球的个数；（请通过列式或列方程解答）随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）19．（8分）综合与探究如图1，平面直角坐标系中，抛物线y=ax2+bx+3与x轴分别交于点A（﹣2，0），B（4，0），与y轴交于点C，点D是y轴负半轴上一点，直线BD与抛物线y=ax2+bx+3在第三象限交于点E（﹣4，y）点F是抛物线y=ax2+bx+3上的一点，且点F在直线BE上方，将点F沿平行于x轴的直线向右平移m个单位长度后恰好落在直线BE上的点G处．（1）求抛物线y=ax2+bx+3的表达式，并求点E的坐标；（2）设点F的横坐标为x（﹣4＜x＜4），解决下列问题：①当点G与点D重合时，求平移距离m的值；②用含x的式子表示平移距离m，并求m的最大值；（3）如图2，过点F作x轴的垂线FP，交直线BE于点P，垂足为F，连接FD．是否存在点F，使△FDP与△FDG的面积比为1：2？若存在，直接写出点F的坐标；若不存在，说明理由．20．（8分）在Rt△ABC中，∠ACB＝90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．(1)求证：AC是⊙O的切线；(2)若BF＝6，⊙O的半径为5，求CE的长．21．（8分）正方形ABCD的边长为3，点E，F分别在射线DC，DA上运动，且DE=DF．连接BF，作EH⊥BF所在直线于点H，连接CH．（1）如图1，若点E是DC的中点，CH与AB之间的数量关系是______；（2）如图2，当点E在DC边上且不是DC的中点时，（1）中的结论是否成立？若成立给出证明；若不成立，说明理由；（3）如图3，当点E，F分别在射线DC，DA上运动时，连接DH，过点D作直线DH的垂线，交直线BF于点K，连接CK，请直接写出线段CK长的最大值．22．（10分）已知关于x的一元二次方程x2+(2m+3)x+m2＝1有两根α，β求m的取值范围；若α+β+αβ＝1．求m的值．23．（12分）某学校环保志愿者协会对该市城区的空气质量进行调查，从全年365天中随机抽取了80天的空气质量指数（AQI）数据，绘制出三幅不完整的统计图表，请根据图表中提供的信息解答下列问题：AQI指数质量等级天数（天）0-50优m51-100良44101-150轻度污染n151-200中度污染4201-300重度污染2300以上严重污染2（1）统计表中m=        ，n=         ，扇形统计图中，空气质量等级为“良”的天数占       %；（2）补全条形统计图，并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少？24．甲班有45人，乙班有39人．现在需要从甲、乙班各抽调一些同学去参加歌咏比赛．如果从甲班抽调的人数比乙班多1人，那么甲班剩余人数恰好是乙班剩余人数的2倍．请问从甲、乙两班各抽调了多少参加歌咏比赛？


参考答案 一、选择题（共10小题，每小题3分，共30分）1、B【解析】【分析】根据有理数是有限小数或无限循环小数，结合无理数的定义进行判断即可得答案．【详解】A、π是无限不循环小数，属于无理数，故本选项错误；B、0是有理数，故本选项正确；C、是无理数，故本选项错误；D、是无理数，故本选项错误，故选B．【点睛】本题考查了实数的分类，熟知有理数是有限小数或无限循环小数是解题的关键．2、D【解析】A．=2，是有理数；B．=2，是有理数；C．，是有理数；D．，是无理数，故选D.3、D【解析】
根据边长确定三角形为直角三角形,斜边即为外切圆直径,内切圆半径为,【详解】解：如下图,∵△ABC的三条边长分别是5，13，12，且52+122=132,∴△ABC是直角三角形,其斜边为外切圆直径,∴外切圆半径==6.5,内切圆半径==2,故选D.【点睛】本题考查了直角三角形内切圆和外切圆的半径,属于简单题,熟悉概念是解题关键.4、B【解析】考点：概率公式．专题：计算题．分析：根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．解答：解：从1、2、3、4、5、6这六个数中随机取出一个数，共有6种情况，取出的数是3的倍数的可能有3和6两种，故概率为2/ 6 ="1/" 3 ．故选B．点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）="m" /n ．5、D【解析】
根据题意可以用相应的代数式表示出去年二月份之前房价，本题得以解决．【详解】由题意可得，去年二月份之前房价为：x÷(1﹣30%)÷(1+40%)=，故选：D．【点睛】本题考查了列代数式，解答本题的关键是明确题意，列出相应的代数式．6、B【解析】
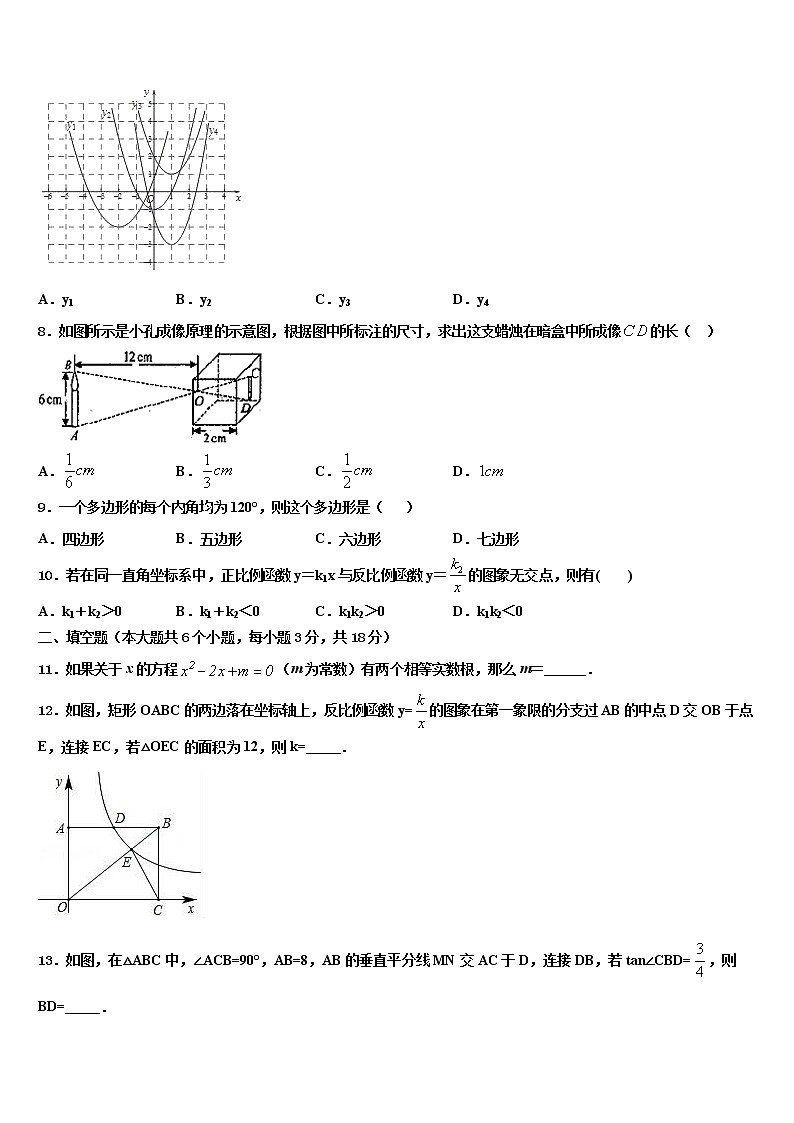
首先分别解出两个不等式,再确定不等式组的解集,然后在数轴上表示即可.【详解】解：解第一个不等式得：x＞-1；解第二个不等式得：x≤1，在数轴上表示，故选B.【点睛】此题主要考查了解一元一次不等式组,以及在数轴上表示解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时 “≥” ,“≤” 要用实心圆点表示; “ <“ >” 要用空心圆点表示.7、A【解析】
由图象的点的坐标，根据待定系数法求得解析式即可判定．【详解】由图象可知：抛物线y1的顶点为（-2，-2），与y轴的交点为（0，1），根据待定系数法求得y1=（x+2）2-2；抛物线y2的顶点为（0，-1），与x轴的一个交点为（1，0），根据待定系数法求得y2=x2-1；抛物线y3的顶点为（1，1），与y轴的交点为（0，2），根据待定系数法求得y3=（x-1）2+1；抛物线y4的顶点为（1，-3），与y轴的交点为（0，-1），根据待定系数法求得y4=2（x-1）2-3；综上，解析式中的二次项系数一定小于1的是y1故选A．【点睛】本题考查了二次函数的图象，二次函数的性质以及待定系数法求二次函数的解析式，根据点的坐标求得解析式是解题的关键．8、D【解析】
过O作直线OE⊥AB，交CD于F，由CD//AB可得△OAB∽△OCD，根据相似三角形对应边的比等于对应高的比列方程求出CD的值即可.【详解】过O作直线OE⊥AB，交CD于F，∵AB//CD，∴OF⊥CD，OE=12，OF=2，∴△OAB∽△OCD，∵OE、OF分别是△OAB和△OCD的高，∴，即，解得：CD=1.故选D.【点睛】本题考查相似三角形的应用，解题的关键在于理解小孔成像原理给我们带来的已知条件，熟记相似三角形对应边的比等于对应高的比是解题关键.9、C【解析】由题意得，180°(n-2)=120°,解得n=6.故选C.10、D【解析】当k1，k2同号时，正比例函数y＝k1x与反比例函数y＝的图象有交点；当k1，k2异号时，正比例函数y＝k1x与反比例函数y＝的图象无交点，即可得当k1k2＜0时，正比例函数y＝k1x与反比例函数y＝的图象无交点，故选D. 二、填空题（本大题共6个小题，每小题3分，共18分）11、1【解析】析：本题需先根据已知条件列出关于m的等式，即可求出m的值．解答：解：∵x的方程x2-2x+m=0（m为常数）有两个相等实数根∴△=b2-4ac=（-2）2-4×1?m=04-4m=0m=1故答案为112、12．【解析】
设AD=a，则AB=OC=2a，根据点D在反比例函数y=的图象上，可得D点的坐标为（a，），所以OA=；过点E 作EN⊥OC于点N，交AB于点M，则OA=MN=,已知△OEC的面积为12，OC=2a，根据三角形的面积公式求得EN=，即可求得EM=；设ON=x，则NC=BM=2a-x，证明△BME∽△ONE，根据相似三角形的性质求得x=，即可得点E的坐标为(，)，根据点E在在反比例函数y=的图象上，可得·=k，解方程求得k值即可.【详解】设AD=a，则AB=OC=2a，∵点D在反比例函数y=的图象上，∴D（a，），∴OA=,过点E 作EN⊥OC于点N，交AB于点M，则OA=MN=,∵△OEC的面积为12，OC=2a，∴EN=，∴EM=MN-EN=-=；设ON=x，则NC=BM=2a-x，∵AB∥OC，∴△BME∽△ONE，∴,即，解得x=，∴E(，)，∵点E在在反比例函数y=的图象上，∴·=k，解得k=，∵k＞0，∴k=12.故答案为：12.【点睛】本题是反比例函数与几何的综合题，求得点E的坐标为(，)是解决问题的关键.13、2．【解析】
由tan∠CBD== 设CD=3a、BC=4a，据此得出BD=AD=5a、AC=AD+CD=8a，由勾股定理可得（8a）2+（4a）2=82，解之求得a的值可得答案．【详解】解：在Rt△BCD中，∵tan∠CBD==，
∴设CD=3a、BC=4a，
则BD=AD=5a，
∴AC=AD+CD=5a+3a=8a，
在Rt△ABC中，由勾股定理可得（8a）2+（4a）2=82，
解得：a= 或a=-（舍），
则BD=5a=2，
故答案为2．【点睛】本题考查线段垂直平分线上的点到线段两端点的距离相等的性质，勾股定理的应用，解题关键是熟记性质与定理并准确识图．14、【解析】
根据被开方式是非负数列式求解即可.【详解】依题意，得，解得：，故答案为：．【点睛】本题考查了函数自变量的取值范围，函数有意义时字母的取值范围一般从几个方面考虑：①当函数解析式是整式时，字母可取全体实数；②当函数解析式是分式时，考虑分式的分母不能为0；③当函数解析式是二次根式时，被开方数为非负数．④对于实际问题中的函数关系式，自变量的取值除必须使表达式有意义外，还要保证实际问题有意义．15、60°或120°．【解析】
连接OA、OB，根据切线的性质得出∠OAP的度数，∠OBP的度数；再根据四边形的内角和是360°，求出∠AOB的度数，有圆周角定理或圆内接四边形的性质，求出∠ACB的度数即可．【详解】解：连接OA、OB．∵PA，PB分别切⊙O于点A，B，∴OA⊥PA，OB⊥PB；∴∠PAO=∠PBO=90°；又∵∠APB=60°，∴在四边形AOBP中，∠AOB=360°﹣90°﹣90°﹣60°=120°，∴ 即当C在D处时，∠ACB=60°．在四边形ADBC中，∠ACB=180°﹣∠ADB=180°﹣60°=120°．于是∠ACB的度数为60°或120°，故答案为60°或120°．【点睛】本题考查的是切线的性质定理，圆内接四边形的性质，是一道基础题．16、；    答案见解析．    【解析】
（1）AB==．故答案为．（2）如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N，G．连接DN，EM，DG，DN与EM相交于点P，点P即为所求．理由：平行四边形ABME的面积：平行四边形CDNB的面积：平行四边形DEMG的面积=1：2：1，△PAB的面积=平行四边形ABME的面积，△PBC的面积=平行四边形CDNB的面积，△PAC的面积=△PNG的面积=△DGN的面积=平行四边形DEMG的面积，∴S△PAB：S△PBC：S△PCA=1：2：1． 三、解答题（共8题，共72分）17、（1）40;（2）想去D景点的人数是8，圆心角度数是72°;（3）280.【解析】
（1）用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数；（2）先计算出最想去D景点的人数，再补全条形统计图，然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“醉美旅游景点D”的扇形圆心角的度数；（3）用800乘以样本中最想去B景点的人数所占的百分比即可．【详解】（1）被调查的学生总人数为8÷20%=40（人）；（2）最想去D景点的人数为40-8-14-4-6=8（人），补全条形统计图为：扇形统计图中表示“醉美旅游景点D”的扇形圆心角的度数为×360°=72°；（3）800×=280，所以估计“醉美旅游景点B“的学生人数为280人．【点睛】本题考查了条形统计图：条形统计图是用线段长度表示数据，根据数量的多少画成长短不同的矩形直条，然后按顺序把这些直条排列起来．从条形图可以很容易看出数据的大小，便于比较．也考查了扇形统计图和利用样本估计总体．18、（1）袋子中白球有2个；（2）见解析， .【解析】
（1）首先设袋子中白球有x个，利用概率公式求即可得方程：，解此方程即可求得答案；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次都摸到相同颜色的小球的情况，再利用概率公式即可求得答案．【详解】解：（1）设袋子中白球有x个，根据题意得：，解得：x＝2，经检验，x＝2是原分式方程的解，∴袋子中白球有2个；（2）画树状图得：∵共有9种等可能的结果，两次都摸到相同颜色的小球的有5种情况，∴两次都摸到相同颜色的小球的概率为：．【点睛】此题考查了列表法或树状图法求概率．注意掌握方程思想的应用．注意概率=所求情况数与总情况数之比．19、（3）（﹣4，﹣6）；（3）①-3；②4；（2）F的坐标为（﹣3，0）或（﹣3，）．【解析】
（3）先将A（﹣3，0），B（4，0），代入y=ax3+bx+2求出a，b的值即可求出抛物线的表达式，再将E点坐标代入表达式求出y的值即可；（3）①设直线BD的表达式为y=kx+b，将B（4，0），E（﹣4，﹣6）代入求出k，b的值，再将x=0代入表达式求出D点坐标，当点G与点D重合时，可得G点坐标，GF∥x轴，故可得F的纵坐标， 再将y=﹣2代入抛物线的解析式求解可得点F的坐标，再根据m=FG即可得m的值；②设点F与点G的坐标，根据m=FG列出方程化简可得出m的二次函数关系式，再根据二次函数的图象可得m的取值范围；（2）分别分析当点F在x轴的左侧时与右侧时的两种情况，根据△FDP与△FDG的面积比为3：3，故PD：DG=3：3．已知FP∥HD，则FH：HG=3：3．再分别设出F,G点的坐标，再根据两点关系列出等式化简求解即可得F的坐标.【详解】解：（3）将A（﹣3，0），B（4，0），代入y=ax3+bx+2得：，解得：，∴抛物线的表达式为y=﹣x3+x+2，把E（﹣4，y）代入得：y=﹣6，∴点E的坐标为（﹣4，﹣6）．（3）①设直线BD的表达式为y=kx+b，将B（4，0），E（﹣4，﹣6）代入得：，解得：，∴直线BD的表达式为y=x﹣2．把x=0代入y=x﹣2得：y=﹣2，∴D（0，﹣2）．当点G与点D重合时，G的坐标为（0，﹣2）．∵GF∥x轴，∴F的纵坐标为﹣2．将y=﹣2代入抛物线的解析式得：﹣x3+x+2=﹣2，解得：x=+3或x=﹣+3．∵﹣4＜x＜4，∴点F的坐标为（﹣+3，﹣2）．∴m=FG=﹣3．②设点F的坐标为（x，﹣x3+x+2），则点G的坐标为（x+m，（x+m）﹣2），∴﹣x3+x+2=（x+m）﹣2，化简得，m=﹣x3+4，∵﹣＜0，∴m有最大值，当x=0时，m的最大值为4．（2）当点F在x轴的左侧时，如下图所示：∵△FDP与△FDG的面积比为3：3，∴PD：DG=3：3．∵FP∥HD，∴FH：HG=3：3．设F的坐标为（x，﹣x3+x+2），则点G的坐标为（﹣3x，﹣x﹣2），∴﹣x3+x+2=﹣x﹣2，整理得：x3﹣6x﹣36=0，解得：x=﹣3或x=4（舍去），∴点F的坐标为（﹣3，0）．当点F在x轴的右侧时，如下图所示：∵△FDP与△FDG的面积比为3：3，∴PD：DG=3：3．∵FP∥HD，∴FH：HG=3：3．设F的坐标为（x，﹣x3+x+2），则点G的坐标为（3x， x﹣2），∴﹣x3+x+2=x﹣2，整理得：x3+3x﹣36=0，解得：x=﹣3或x=﹣﹣3（舍去），∴点F的坐标为（﹣3，）．综上所述，点F的坐标为（﹣3，0）或（﹣3，）．【点睛】本题考查了二次函数的应用，解题的关键是熟练的掌握二次函数的应用.20、（1）证明见解析；（2）CE=1．【解析】
（1）根据等角对等边得∠OBE=∠OEB，由角平分线的定义可得∠OBE=∠EBC，从而可得∠OEB=∠EBC，根据内错角相等，两直线平行可得OE∥BC，根据两直线平行，同位角相等可得∠OEA=90°，从而可证AC是⊙O的切线.
（2）根据垂径定理可求BH=BF=3，根据三个角是直角的四边形是矩形，可得四边形OHCE是矩形，由矩形的对边相等可得CE=OH，在Rt△OBH中，利用勾股定理可求出OH的长，从而求出CE的长.【详解】（1）证明：如图，连接OE，

∵OB=OE，
∴∠OBE=∠OEB，
∵ BE平分∠ABC．
∴∠OBE=∠EBC，
∴∠OEB=∠EBC，
∴OE∥BC，
∵ ∠ACB=90° ，
∴∠OEA=∠ACB=90°，
∴ AC是⊙O的切线 .
（2）解：过O作OH⊥BF，
∴BH=BF=3，四边形OHCE是矩形，
∴CE=OH，
在Rt△OBH中，BH=3，OB=5，
∴OH==1，
∴CE=1.【点睛】本题考查切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线和垂径定理以及勾股定理的运用，具有一定的综合性．21、（1）CH=AB．；（2）成立，证明见解析；（3）【解析】
（1）首先根据全等三角形判定的方法，判断出△ABF≌△CBE，即可判断出∠1=∠2；然后根据EH⊥BF，∠BCE=90°，可得C、H两点都在以BE为直径的圆上，判断出∠4=∠HBC，即可判断出CH=BC，最后根据AB=BC，判断出CH=AB即可．（2）首先根据全等三角形判定的方法，判断出△ABF≌△CBE，即可判断出∠1=∠2；然后根据EH⊥BF，∠BCE=90°，可得C、H两点都在以BE为直径的圆上，判断出∠4=∠HBC，即可判断出CH=BC，最后根据AB=BC，判断出CH=AB即可．（3）首先根据三角形三边的关系，可得CK＜AC+AK，据此判断出当C、A、K三点共线时，CK的长最大；然后根据全等三角形判定的方法，判断出△DFK≌△DEH，即可判断出DK=DH，再根据全等三角形判定的方法，判断出△DAK≌△DCH，即可判断出AK=CH=AB；最后根据CK=AC+AK=AC+AB，求出线段CK长的最大值是多少即可．【详解】解：（1）如图1，连接BE，，在正方形ABCD中，AB=BC=CD=AD，∠A=∠BCD=∠ABC=90°，∵点E是DC的中点，DE=EC，∴点F是AD的中点，∴AF=FD，∴EC=AF，在△ABF和△CBE中，∴△ABF≌△CBE，∴∠1=∠2，∵EH⊥BF，∠BCE=90°，∴C、H两点都在以BE为直径的圆上，∴∠3=∠2，∴∠1=∠3，∵∠3+∠4=90°，∠1+∠HBC=90°，∴∠4=∠HBC，∴CH=BC，又∵AB=BC，∴CH=AB．（2）当点E在DC边上且不是DC的中点时，（1）中的结论CH=AB仍然成立．如图2，连接BE，，在正方形ABCD中，AB=BC=CD=AD，∠A=∠BCD=∠ABC=90°，∵AD=CD，DE=DF，∴AF=CE，在△ABF和△CBE中， ∴△ABF≌△CBE，∴∠1=∠2，∵EH⊥BF，∠BCE=90°，∴C、H两点都在以BE为直径的圆上，∴∠3=∠2，∴∠1=∠3，∵∠3+∠4=90°，∠1+∠HBC=90°，∴∠4=∠HBC，∴CH=BC，又∵AB=BC，∴CH=AB．（3）如图3，，∵CK≤AC+AK，∴当C、A、K三点共线时，CK的长最大，∵∠KDF+∠ADH=90°，∠HDE+∠ADH=90°，∴∠KDF=∠HDE，∵∠DEH+∠DFH=360°-∠ADC-∠EHF=360°-90°-90°=180°，∠DFK+∠DFH=180°，∴∠DFK=∠DEH，在△DFK和△DEH中，∴△DFK≌△DEH，∴DK=DH，在△DAK和△DCH中，∴△DAK≌△DCH，∴AK=CH又∵CH=AB，∴AK=CH=AB，∵AB=3，∴AK=3，AC=3，∴CK=AC+AK=AC+AB=，即线段CK长的最大值是．考点：四边形综合题．22、 (1)m≥﹣；(2)m的值为2．【解析】
（1）根据方程有两个相等的实数根可知△＞1，求出m的取值范围即可；（2）根据根与系数的关系得出α+β与αβ的值，代入代数式进行计算即可．【详解】(1)由题意知，(2m+2)2﹣4×1×m2≥1，解得：m≥﹣；(2)由根与系数的关系得：α+β＝﹣(2m+2)，αβ＝m2，∵α+β+αβ＝1，∴﹣(2m+2)+m2＝1，解得：m1＝﹣1，m1＝2，由(1)知m≥﹣，所以m1＝﹣1应舍去，m的值为2．【点睛】本题考查的是根与系数的关系，熟知x1，x2是一元二次方程ax2+bx+c＝1（a≠1）的两根时，x1+x2＝﹣，x1x2＝是解答此题的关键．23、 (1)m=20,n=8；55;(2) 答案见解析.【解析】
（1）由A占25%，即可求得m的值，继而求得n的值，然后求得空气质量等级为“良”的天数占的百分比；（2）首先由（1）补全统计图，然后利用样本估计总体的知识求解即可求得答案.【详解】（1）∵m=80×25%=20，n=80-20-44-4-2-2=8，∴空气质量等级为“良”的天数占：×100%=55%.故答案为20，8,55；（2）估计该市城区全年空气质量等级为“优”和“良”的天数共：365×（25%+55%）=292（天），答：估计该市城区全年空气质量等级为“优”和“良”的天数共292天；补全统计图：【点睛】此题考查了条形图与扇形图的知识．读懂统计图，从统计图中得到必要的信息是解决问题的关键．24、从甲班抽调了35人，从乙班抽调了1人【解析】分析：首先设从甲班抽调了x人，那么从乙班抽调了（x﹣1）人，根据题意列出一元一次方程，从而得出答案．详解：设从甲班抽调了x人，那么从乙班抽调了（x﹣1）人， 由题意得，45﹣x=2[39﹣（x﹣1）]，     解得：x=35，  则x﹣1=35﹣1=1．              答：从甲班抽调了35人，从乙班抽调了1人．    点睛：本题主要考查的是一元一次方程的应用，属于基础题型．理解题目的含义，找出等量关系是解题的关键．