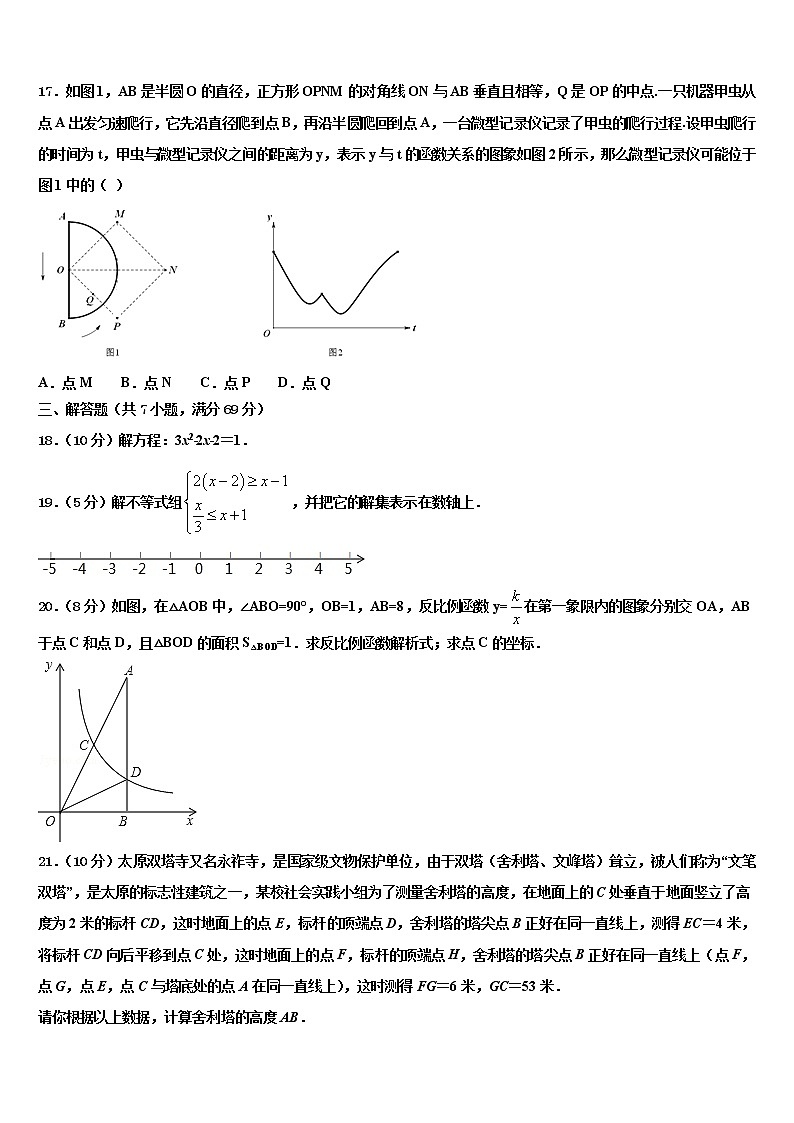
辽宁省皇姑区达标名校2021-2022学年中考适应性考试数学试题含解析

这是一份辽宁省皇姑区达标名校2021-2022学年中考适应性考试数学试题含解析，共16页。试卷主要包含了考生必须保证答题卡的整洁，在同一平面内，下列说法，下列计算正确的有个等内容，欢迎下载使用。
2021-2022中考数学模拟试卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．分式方程的解为（  ）A．x=-2 B．x=-3 C．x=2 D．x=32．已知点M (－2，3 )在双曲线上，则下列一定在该双曲线上的是（ ）A．(3，-2 ) B．(-2，-3 ) C．(2，3 ) D．(3，2)3．已知反比例函数y=的图象位于第一、第三象限，则k的取值范围是（　　）A．k＞8 B．k≥8 C．k≤8 D．k＜84．在同一平面内，下列说法：①过两点有且只有一条直线；②两条不相同的直线有且只有一个公共点；③经过直线外一点有且只有一条直线与已知直线垂直；④经过直线外一点有且只有一条直线与已知直线平行，其中正确的个数为（   ）A．1个 B．2个 C．3个 D．4个5．如图，由两个相同的正方体和一个圆锥体组成一个立体图形，其俯视图是A． B． C． D．6．不等式5+2x ＜1的解集在数轴上表示正确的是(     ).A． B． C． D．7．在实数，，，中，其中最小的实数是（　　）A． B． C． D．8．下列计算正确的有（     ）个①（﹣2a2）3＝﹣6a6   ②（x﹣2）（x+3）＝x2﹣6    ③（x﹣2）2＝x2﹣4 ④﹣2m3+m3＝﹣m3      ⑤﹣16＝﹣1．A．0 B．1 C．2 D．39．若点A(1，a)和点B(4，b)在直线y＝－2x＋m上，则a与b的大小关系是(　　)A．a＞b B．a＜bC．a＝b D．与m的值有关10．一副直角三角板如图放置，其中，，，点F在CB的延长线上若，则等于（    ）A．35° B．25° C．30° D．15°二、填空题（共7小题，每小题3分，满分21分）11．在2018年帮助居民累计节约用水305000吨，将数字305000用科学记数法表示为_____．12．如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是___．13．已知一纸箱中，装有5个只有颜色不同的球，其中2个白球，3个红球，若往原纸箱中再放入x个白球，然后从箱中随机取出一个白球的概率是，则x的值为_____14．已知∠=32°，则∠的余角是_____°．15．如图，⊙M的半径为2，圆心M（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为_____．16．不等式组的解集是_____；17．如图1，AB是半圆O的直径，正方形OPNM的对角线ON与AB垂直且相等，Q是OP的中点.一只机器甲虫从点A出发匀速爬行，它先沿直径爬到点B，再沿半圆爬回到点A，一台微型记录仪记录了甲虫的爬行过程.设甲虫爬行的时间为t，甲虫与微型记录仪之间的距离为y，表示y与t的函数关系的图象如图2所示，那么微型记录仪可能位于图1中的（ ）A．点M    B．点N    C．点P    D．点Q三、解答题（共7小题，满分69分）18．（10分）解方程：3x2﹣2x﹣2＝1．19．（5分）解不等式组，并把它的解集表示在数轴上．20．（8分）如图，在△AOB中，∠ABO=90°，OB=1，AB=8，反比例函数y=在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=1．求反比例函数解析式；求点C的坐标．21．（10分）太原双塔寺又名永祚寺，是国家级文物保护单位，由于双塔（舍利塔、文峰塔）耸立，被人们称为“文笔双塔”，是太原的标志性建筑之一，某校社会实践小组为了测量舍利塔的高度，在地面上的C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，舍利塔的塔尖点B正好在同一直线上，测得EC＝4米，将标杆CD向后平移到点C处，这时地面上的点F，标杆的顶端点H，舍利塔的塔尖点B正好在同一直线上（点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得FG＝6米，GC＝53米．请你根据以上数据，计算舍利塔的高度AB．22．（10分）如图，已知A（﹣4，n），B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数y＝的图象的两个交点．求反比例函数和一次函数的解析式；求直线AB与x轴的交点C的坐标及△AOB的面积；直接写出一次函数的值小于反比例函数值的x的取值范围．23．（12分）如图，A，B，C 三个粮仓的位置如图所示，A 粮仓在 B 粮仓北偏东26°，180 千米处；C 粮仓在 B 粮仓的正东方，A 粮仓的正南方．已知 A，B两个粮仓原有存粮共 450 吨，根据灾情需要，现从 A 粮仓运出该粮仓存粮的支援 C 粮仓，从 B 粮仓运出该粮仓存粮的支援 C 粮仓，这时 A，B 两处粮仓的存粮吨数相等．（tan26°＝0.44，cos26°＝0.90，tan26°＝0.49）（1）A，B 两处粮仓原有存粮各多少吨？（2）C 粮仓至少需要支援 200 吨粮食，问此调拨计划能满足 C 粮仓的需求吗？（3）由于气象条件恶劣，从 B 处出发到 C 处的车队来回都限速以每小时 35 公里的速度匀速行驶，而司机小王的汽车油箱的油量最多可行驶 4 小时，那么小王在途中是否需要加油才能安全的回到 B 地？请你说明理由．24．（14分）为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？


参考答案 一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1、B【解析】解：去分母得：2x=x﹣3，解得：x=﹣3，经检验x=﹣3是分式方程的解．故选B．2、A【解析】因为点M（-2，3）在双曲线上，所以xy=（-2）×3=-6，四个答案中只有A符合条件．故选A3、A【解析】
本题考查反比例函数的图象和性质，由k-8＞0即可解得答案．【详解】∵反比例函数y=的图象位于第一、第三象限，∴k-8＞0，解得k＞8，故选A．【点睛】本题考查了反比例函数的图象和性质：①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．4、C【解析】
根据直线的性质公理，相交线的定义，垂线的性质，平行公理对各小题分析判断后即可得解．【详解】解:在同一平面内，①过两点有且只有一条直线，故①正确；②两条不相同的直线相交有且只有一个公共点，平行没有公共点，故②错误；③在同一平面内，经过直线外一点有且只有一条直线与已知直线垂直，故③正确；④经过直线外一点有且只有一条直线与已知直线平行，故④正确，综上所述，正确的有①③④共3个，故选C．【点睛】本题考查了平行公理，直线的性质，垂线的性质，以及相交线的定义，是基础概念题，熟记概念是解题的关键．5、D【解析】
由圆锥的俯视图可快速得出答案.【详解】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中，从几何体的上面看：可以得到两个正方形，右边的正方形里面有一个内接圆.故选D.【点睛】本题考查立体图形的三视图，熟记基本立体图的三视图是解题的关键.6、C【解析】
先解不等式得到x＜-1，根据数轴表示数的方法得到解集在-1的左边．【详解】5+1x＜1，移项得1x＜-4，系数化为1得x＜-1．故选C．【点睛】本题考查了在数轴上表示不等式的解集：先求出不等式组的解集，然后根据数轴表示数的方法把对应的未知数的取值范围通过画区间的方法表示出来，等号时用实心，不等时用空心．7、B【解析】
由正数大于一切负数，负数小于0，正数大于0，两个负数绝对值大的反而小，把这四个数从小到大排列，即可求解．【详解】解：∵0，-2，1，中，-2＜0＜1＜，
∴其中最小的实数为-2；
故选：B．【点睛】本题考查了实数的大小比较，关键是掌握：正数大于0，负数小于0，正数大于一切负数，两个负数绝对值大的反而小．8、C【解析】
根据积的乘方法则，多项式乘多项式的计算法则，完全平方公式，合并同类项的计算法则，乘方的定义计算即可求解．【详解】①（﹣2a2）3=﹣8a6，错误；②（x﹣2）（x+3）=x2+x﹣6，错误；③（x﹣2）2=x2﹣4x+4，错误④﹣2m3+m3=﹣m3，正确；⑤﹣16=﹣1，正确．计算正确的有2个．故选C．【点睛】考查了积的乘方，多项式乘多项式，完全平方公式，合并同类项，乘方，关键是熟练掌握计算法则正确进行计算．9、A【解析】【分析】根据一次函数性质：中，当k>0时，y随x的增大而增大；当k<0时，y随x的增大而减小.由-2<0得，当x12时，y1>y2.【详解】因为，点A(1，a)和点B(4，b)在直线y＝－2x＋m上，-2<0,所以，y随x的增大而减小.因为，1<4,所以，a>b.故选A【点睛】本题考核知识点：一次函数性质. 解题关键点:判断一次函数中y与x的大小关系，关键看k的符号.10、D【解析】
直接利用三角板的特点，结合平行线的性质得出∠BDE=45°，进而得出答案．【详解】解：由题意可得：∠EDF=30°，∠ABC=45°，
∵DE∥CB，
∴∠BDE=∠ABC=45°，
∴∠BDF=45°-30°=15°．
故选D．【点睛】此题主要考查了平行线的性质，根据平行线的性质得出∠BDE的度数是解题关键． 二、填空题（共7小题，每小题3分，满分21分）11、3.05×105【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>10时，n是正数；当原数的绝对值<1时，n是负数．【详解】故答案为：.【点睛】本题考查的知识点是科学记数法—表示较大的数，解题关键是熟记科学计数法的表示方法.12、12【解析】
根据图象可知点P在BC上运动时，此时BP不断增大，而从C向A运动时，BP先变小后变大，从而可求出线段长度解答．【详解】根据题意观察图象可得BC=5，点P在AC上运动时，BPAC时，BP有最小值，观察图象可得，BP的最小值为4，即BPAC时BP=4，又勾股定理求得CP=3，因点P从点C运动到点A，根据函数的对称性可得CP=AP=3，所以的面积是=12.【点睛】本题考查动点问题的函数图象，解题的关键是注意结合图象求出线段的长度，本题属于中等题型．13、1．【解析】
先根据概率公式得到，解得.【详解】根据题意得，解得.故答案为：.【点睛】本题考查了概率公式：随机事件的概率事件可能出现的结果数除以所有可能出现的结果数.14、58°【解析】
根据余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角可得答案．【详解】解：∠α的余角是：90°-32°=58°．故答案为58°．【点睛】本题考查余角，解题关键是掌握互为余角的两个角的和为90度．15、6【解析】
点P在以O为圆心OA为半径的圆上，P是两个圆的交点，当⊙O与⊙M外切时，AB最小，根据条件求出AO即可求解；【详解】解：点P在以O为圆心OA为半径的圆上，∴P是两个圆的交点，当⊙O与⊙M外切时，AB最小，∵⊙M的半径为2，圆心M（3，4），∴PM＝5，∴OA＝3，∴AB＝6，故答案为6；【点睛】本题考查圆与圆的位置关系；能够将问题转化为两圆外切时AB最小是解题的关键．16、x≤1【解析】分析：分别求出不等式组中两个不等式的解集，找出解集的公共部分即可确定出不等式组的解集.详解： ，由①得：x由②得：.则不等式组的解集为：x.故答案为x≤1.点睛：本题主要考查了解一元一次不等式组.17、D【解析】D．试题分析：应用排他法分析求解：若微型记录仪位于图1中的点M，AM最小，与图2不符，可排除A.若微型记录仪位于图1中的点N，由于AN=BM，即甲虫从A到B时是对称的，与图2不符，可排除B.若微型记录仪位于图1中的点P，由于甲虫从A到OP与圆弧的交点时甲虫与微型记录仪之间的距离y逐渐减小；甲虫从OP与圆弧的交点到A时甲虫与微型记录仪之间的距离y逐渐增大，即y与t的函数关系的图象只有两个趋势，与图2不符，可排除C.故选D．考点：1.动点问题的函数图象分析；2.排他法的应用. 三、解答题（共7小题，满分69分）18、【解析】
先找出a，b，c，再求出b2-4ac=28，根据公式即可求出答案．【详解】解：x＝ =即∴原方程的解为.【点睛】本题考查对解一元二次方程-提公因式法、公式法，因式分解法等知识点的理解和掌握，能熟练地运用公式法解一元二次方程是解此题的关键．19、不等式组的解是x≥3;图见解析【解析】
先求出每个不等式的解集，再求出不等式组的解集即可．【详解】解：∵解不等式①，得x≥3，解不等式②，得x≥－1.5，∴不等式组的解是x≥3，在数轴上表示为：．【点睛】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集，能根据不等式的解集找出不等式组的解集是解此题的关键．20、（1）反比例函数解析式为y=；（2）C点坐标为（2，1）【解析】
（1）由S△BOD=1可得BD的长，从而可得D的坐标，然后代入反比例函数解析式可求得k，从而得解析式为y=；（2）由已知可确定A点坐标，再由待定系数法求出直线AB的解析式为y=2x，然后解方程组即可得到C点坐标．【详解】（1）∵∠ABO=90°，OB=1，S△BOD=1，∴OB×BD=1，解得BD=2，∴D（1，2）将D（1，2）代入y=,得2=,∴k=8，∴反比例函数解析式为y=；（2）∵∠ABO=90°，OB=1，AB=8，∴A点坐标为（1，8），设直线OA的解析式为y=kx，把A（1，8）代入得1k=8，解得k=2，∴直线AB的解析式为y=2x，解方程组得或，∴C点坐标为（2，1）.21、55米【解析】
由题意可知△EDC∽△EBA，△FHC∽△FBA，根据相似三角形的性质可得，又DC=HG，可得，代入数据即可求得AC=106米，再由即可求得AB=55米.【详解】∵△EDC∽△EBA，△FHC∽△FBA,，，，即，∴AC=106米，又 ，∴，∴AB=55米.答：舍利塔的高度AB为55米．【点睛】本题考查相似三角形的判定和性质的应用，解题的关键是灵活运用所学知识解决问题，利用相似三角形的性质建立方程解决问题．22、（1）y＝﹣x﹣2；（2）C（﹣2，0），△AOB=6，,（3）﹣4＜x＜0或x＞2.【解析】
（1）先把B点坐标代入代入y＝，求出m得到反比例函数解析式，再利用反比例函数解析式确定A点坐标，然后利用待定系数法求一次函数解析式；（2）根据x轴上点的坐标特征确定C点坐标，然后根据三角形面积公式和△AOB的面积＝S△AOC+S△BOC进行计算；（3）观察函数图象得到当﹣4＜x＜0或x＞2时，一次函数图象都在反比例函数图象下方．【详解】解：∵B（2，﹣4）在反比例函数y＝的图象上，∴m＝2×（﹣4）＝﹣8，∴反比例函数解析式为：y＝﹣，把A（﹣4，n）代入y＝﹣，得﹣4n＝﹣8，解得n＝2，则A点坐标为（﹣4，2）．把A（﹣4，2），B（2，﹣4）分别代入y＝kx+b，得，解得，∴一次函数的解析式为y＝﹣x﹣2；（2）∵y＝﹣x﹣2，∴当﹣x﹣2＝0时，x＝﹣2，∴点C的坐标为：（﹣2，0），△AOB的面积＝△AOC的面积+△COB的面积＝×2×2+×2×4＝6；（3）由图象可知，当﹣4＜x＜0或x＞2时，一次函数的值小于反比例函数的值．【点睛】本题考查的是一次函数与反比例函数的交点问题以及待定系数法的运用，灵活运用待定系数法是解题的关键，注意数形结合思想的正确运用．23、（1）A、B 两处粮仓原有存粮分别是 270，1 吨；（2）此次调拨能满足 C 粮仓需求；（3）小王途中须加油才能安全回到 B 地．【解析】
（1）由题意可知要求A，B两处粮仓原有存粮各多少吨需找等量关系，即A处存粮+B处存粮=450吨，A处存粮的五分之二=B处存粮的五分之三，据等量关系列方程组求解即可；（2）分别求出A处和B处支援C处的粮食，将其加起来与200吨比较即可；（3）由题意可知由已知可得△ABC中∠A=26°∠ACB=90°且AB=1Km，sin∠BAC=，要求BC的长，可以运用三角函数解直角三角形．【详解】（1）设A，B两处粮仓原有存粮x，y吨根据题意得： 解得：x=270，y=1．答：A，B两处粮仓原有存粮分别是270，1吨．（2）A粮仓支援C粮仓的粮食是×270=162（吨），B粮仓支援C粮仓的粮食是×1=72（吨），A，B两粮仓合计共支援C粮仓粮食为162+72=234（吨）．∵234＞200，∴此次调拨能满足C粮仓需求．（3）如图，根据题意知：∠A=26°，AB=1千米，∠ACB=90°．在Rt△ABC中，sin∠BAC=，∴BC=AB•sin∠BAC=1×0.44=79.2．∵此车最多可行驶4×35=140（千米）＜2×79.2，∴小王途中须加油才能安全回到B地．【点睛】求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．24、（1）y=﹣20x+1600；（2）当每盒售价定为60元时，每天销售的利润P（元）最大，最大利润是8000元；（3）超市每天至少销售粽子440盒．【解析】试题分析：（1）根据“当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒”即可得出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）根据利润=1盒粽子所获得的利润×销售量列式整理，再根据二次函数的最值问题解答；（3）先由（2）中所求得的P与x的函数关系式，根据这种粽子的每盒售价不得高于58元，且每天销售粽子的利润不低于6000元，求出x的取值范围，再根据（1）中所求得的销售量y（盒）与每盒售价x（元）之间的函数关系式即可求解．试题解析：（1）由题意得，==；（2）P===，∵x≥45，a=﹣20＜0，∴当x=60时，P最大值=8000元，即当每盒售价定为60元时，每天销售的利润P（元）最大，最大利润是8000元；（3）由题意，得=6000，解得，，∵抛物线P=的开口向下，∴当50≤x≤70时，每天销售粽子的利润不低于6000元的利润，又∵x≤58，∴50≤x≤58，∵在中，＜0，∴y随x的增大而减小，∴当x=58时，y最小值=﹣20×58+1600=440，即超市每天至少销售粽子440盒．考点：二次函数的应用．