2021学年1. 矩形的性质背景图ppt课件

这是一份2021学年1. 矩形的性质背景图ppt课件，共19页。PPT课件主要包含了你能写出证明过程吗，练一练，知识回顾等内容，欢迎下载使用。
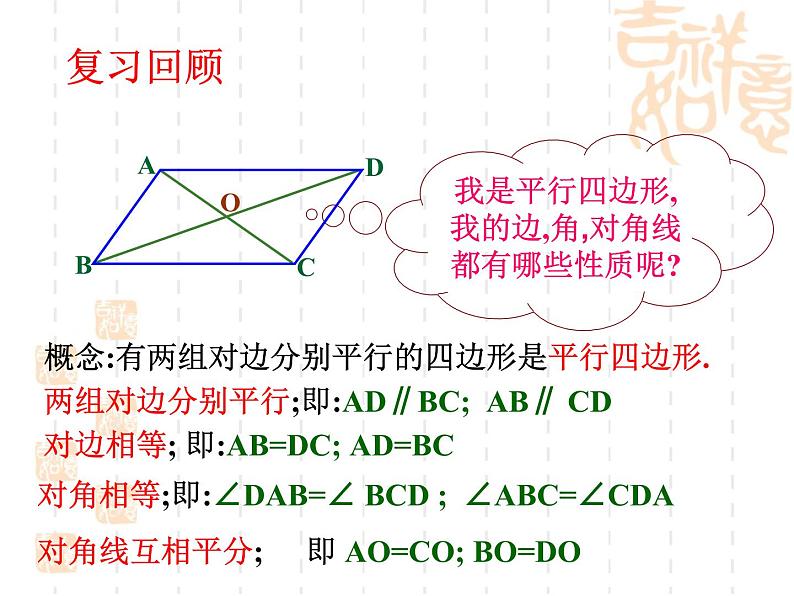
我是平行四边形,我的边,角,对角线都有哪些性质呢?
概念:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC; AB∥ CD
对边相等; 即:AB=DC; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
即 AO=CO; BO=DO
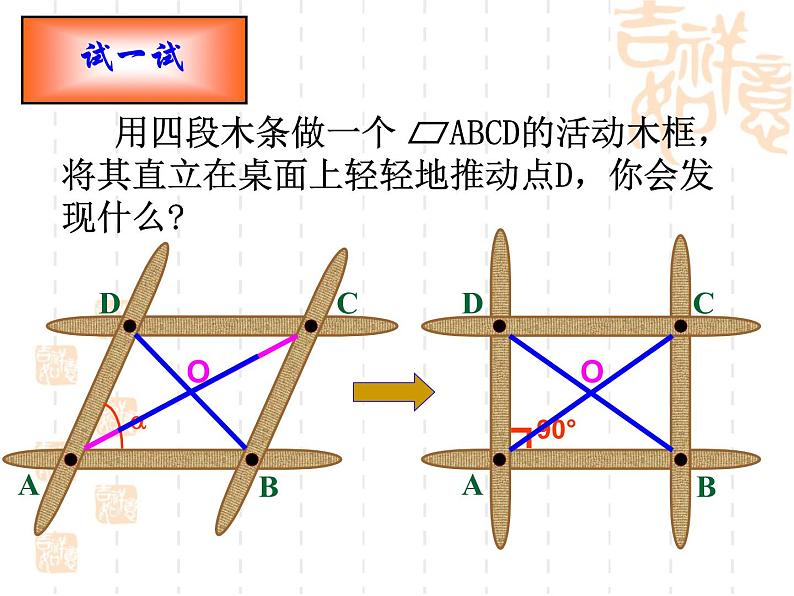
用四段木条做一个 ABCD的活动木框，将其直立在桌面上轻轻地推动点D，你会发现什么?
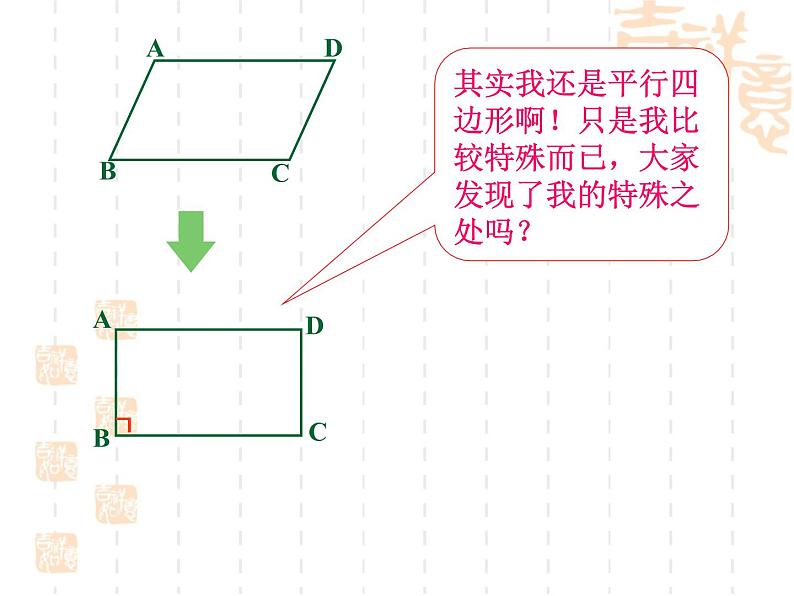
其实我还是平行四边形啊！只是我比较特殊而已，大家发现了我的特殊之处吗？
有一个角是直角的平行四边形。
生活中的矩形图:信兴广场大厦(深圳)
怎样的平行四边形是矩形呢?
2008年国家游泳中心
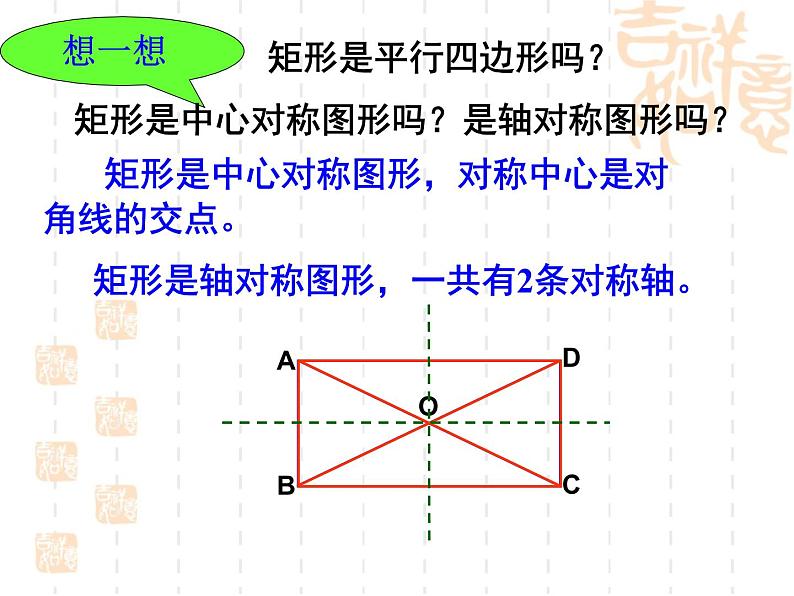
矩形是中心对称图形，对称中心是对角线的交点。
矩形是轴对称图形，一共有2条对称轴。
矩形是中心对称图形吗？是轴对称图形吗？
1.画一个矩形ABCD。
2.从边、角、对角线三方面进行考虑，你能发现矩形有什么特有的性质吗？请以小组的形式讨论总结。
四个角都是直角 　　　　
互相平分 AO＝CO; BO＝DO
平行 AD∥BC; AB∥ CD　　　 　　　　
相等 AB＝CD; AD＝BC　　　 　　　　
相 等 AC＝BD 　　 　　　　
互相垂直 AB⊥BC; AB ⊥ AD AD⊥DC;BC⊥CD
∠BAD＝∠ABC＝∠BCD＝∠CDA＝ 90°
矩形性质1: 矩形的四个内角都是直角.
矩形性质2:矩形的对角线相等．
对于性质1，我们很容易根据矩形的定义和平行四边形角的性质加以证明.
对于性质2，我们可以找到对角线AC、BD分别所在的三角形，借助性质1证明这两个三角形全等，从而得到结论.
例1 如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少？
解：∵ΔAOB、ΔBOC、ΔCOD、ΔAOD四个小三角形的周长的和是86cm
∴AB+BC+CD+DA+2（OA+OB+OC+OD）
=AB+BC+CD+DA+2（AC+BD）
又∵AC=BD=13（矩形的对角线相等）
∴AB+BC+CD+DA=86-2（AC+BD） =86-4×13 =34（cm）
即矩形ABCD的周长为34cm
4.下列性质中，矩形不一定具有的是（ ） A、对角线相等 B、 四个角都相等 C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。2.有一个角是直角的四边形是矩形。（ ）3.矩形的对角线互相平分。（ ）
5.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等 C 对角线互相平分 D 对角线相等
6.矩形ABCD中，对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。（A）2 （B）4 （C）6 （D）8
７.如图，在矩形ABCD中，对角线ＡＣ与BD相交于,找出相等的线段与相等的角．
矩形：有一个角是直角的特殊平行四边形。
4.矩形的对角线相等且互相平分。
1.矩形具有平行四边形的所有性质；
2.矩形既是轴对称图形又是中心对称图形；
3.矩形的四个内角都是直角。