初中数学华师大版八年级下册17.1 变量与函数教学课件ppt

这是一份初中数学华师大版八年级下册17.1 变量与函数教学课件ppt，共15页。PPT课件主要包含了问题一，问题二，问题三，πr2，问题四，2列表法，3图象法，课堂小结等内容，欢迎下载使用。

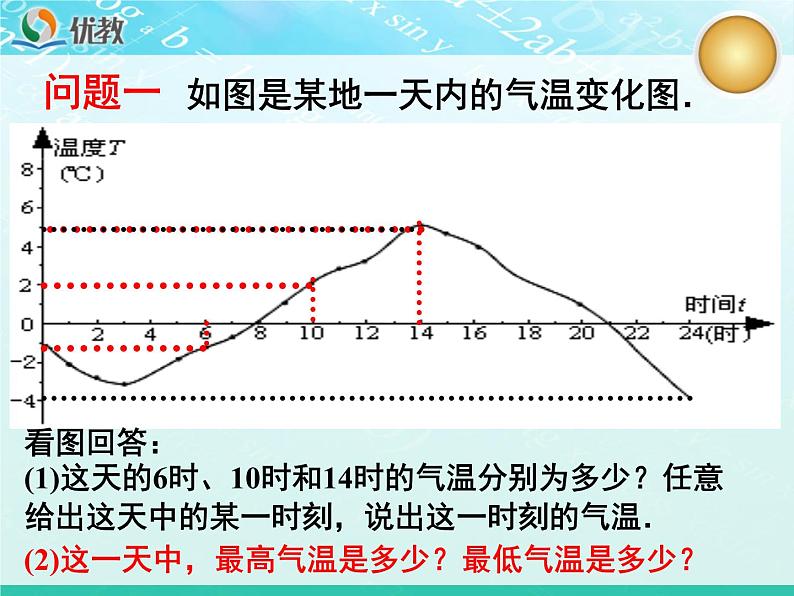
如图是某地一天内的气温变化图．
看图回答：(1)这天的6时、10时和14时的气温分别为多少？任意给出这天中的某一时刻，说出这一时刻的气温．
(2)这一天中，最高气温是多少？最低气温是多少？
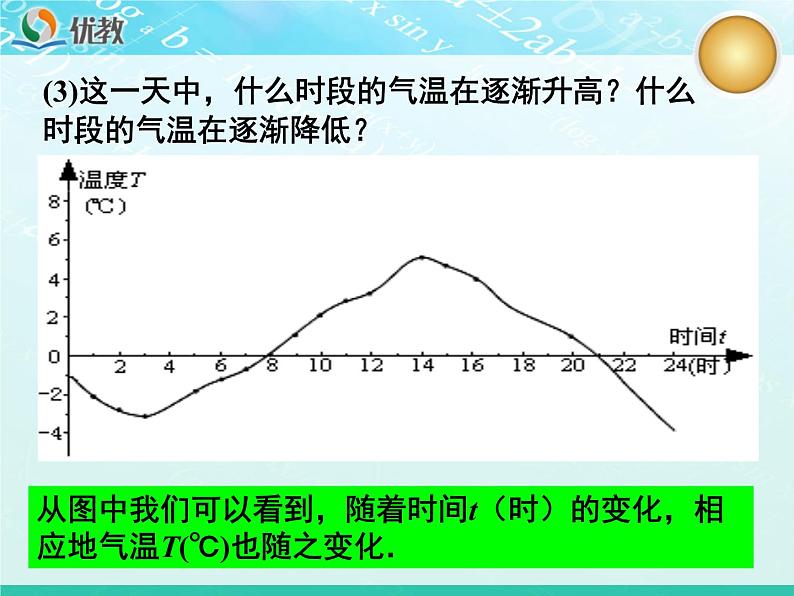
(3)这一天中，什么时段的气温在逐渐升高？什么时段的气温在逐渐降低？
从图中我们可以看到，随着时间t（时）的变化，相应地气温T(℃)也随之变化．
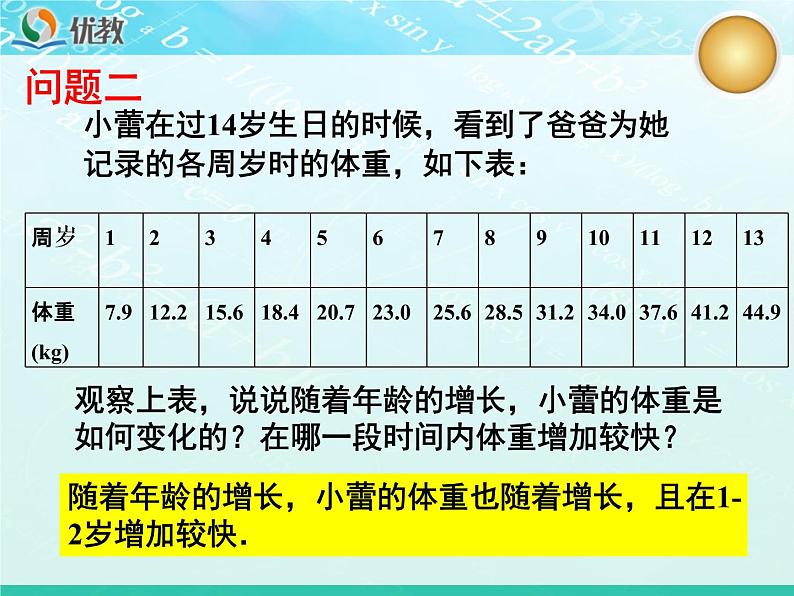
小蕾在过14岁生日的时候，看到了爸爸为她记录的各周岁时的体重，如下表：
观察上表，说说随着年龄的增长，小蕾的体重是如何变化的？在哪一段时间内体重增加较快？
随着年龄的增长，小蕾的体重也随着增长，且在1-2岁增加较快．
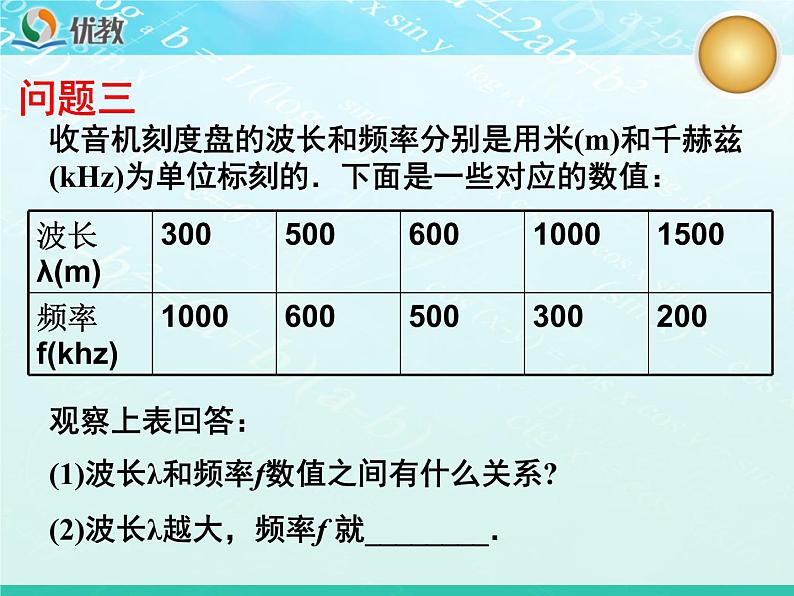
收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的．下面是一些对应的数值：
观察上表回答：(1)波长λ和频率f数值之间有什么关系?(2)波长λ越大，频率f 就________．
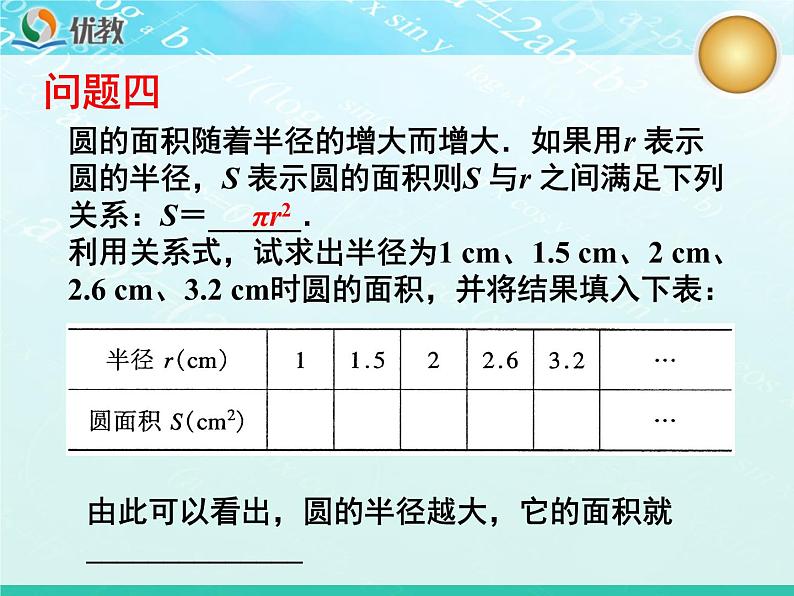
圆的面积随着半径的增大而增大．如果用r 表示圆的半径，S 表示圆的面积则S 与r 之间满足下列关系：S＝______．利用关系式，试求出半径为1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积，并将结果填入下表：
由此可以看出，圆的半径越大，它的面积就______________
在上面的问题中，我们研究了一些数量关系，它们都刻画了某些变化规律．这里出现了各种各样的量，特别值得注意的是出现了一些数值会发生变化的量. 例如问题1中，刻画气温变化规律的量是时间t 和气温T，气温T 随着时间t 的变化而变化，它们都会取不同的数值．
像这样在某一变化过程中，可以取不同数值的量，叫做变量(variable)．
在问题的研究过程中，还有一种量，它的取值始终保持不变，我们称之为常量
上面各个问题中，都出现了两个变量，它们互相依赖，密切相关． 一般地，如果在一个变化过程中，有两个变量，例如x和y，对于x的每一个值，y都有惟一的值与之对应，我们就说x是自变量，y是因变量，此时也称y是x的函数．
表示函数关系的方法通常有三种：
在研究函数时，必须注意自变量的取值范围.实际问题中，自变量的取值必须符合实际意义.例如，上述问题4中，自变量r表示圆的半径，不能为负数和零，即它的取值范围为一切正实数
例1 下表是某市2012年统计的中小学男学生各年龄组的平均身高：
(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?
例2 写出下列各问题中的关系式，并指出自变量的取值范围：(1)圆的周长C 与半径r 的关系式；(2)火车以60千米/时的速度行驶，它驶过的路程s（千米）和所用时间t（时）的关系式；(3)n 边形的内角和 S 与边数 n 的关系式．
1.函数概念包含：(1)两个变量；(2)两个变量之间的对应关系．
2.在某个变化过程中，可以取不同数值的量，叫做变量；数值始终保持不变的量，叫做常量．例如x和y，对于x 的每一个值，y 都有惟一的值与之对应，我们就说x 是自变量，y 是因变量．
3.函数关系三种表示方法：(1)解析法；(2)列表法；(3)图象法．