福建省三明市尤溪县九年级下学期开学考试数学试卷含解析

 九年级下学期开学考试数学试卷

一、选择题：本题共10小题，每小题4分，共40分。

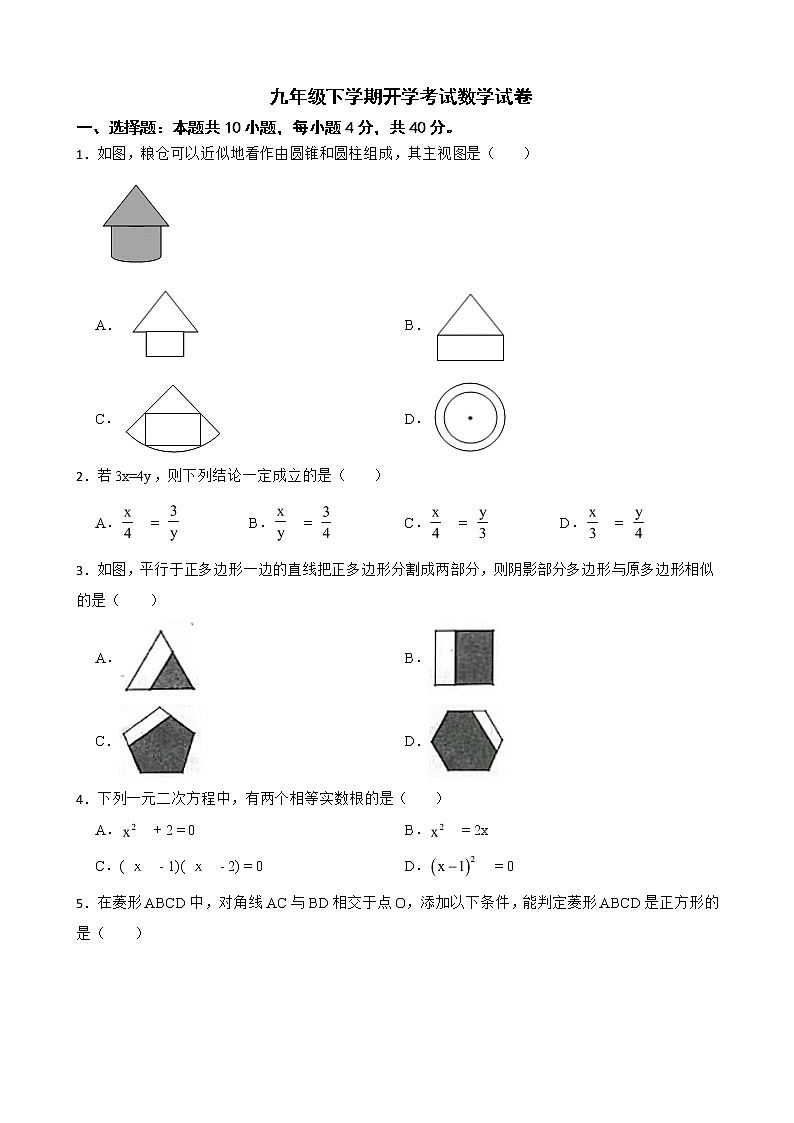
1．如图，粮仓可以近似地看作由圆锥和圆柱组成，其主视图是（　　） 

A． B．

C． D．

2．若3x=4y，则下列结论一定成立的是（　　） 

A．  =  B．  =  C．  =  D．  =

3．如图，平行于正多边形一边的直线把正多边形分割成两部分，则阴影部分多边形与原多边形相似的是（　　） 

A． B．

C． D．

4．下列一元二次方程中，有两个相等实数根的是（　　）  

A．  + 2 = 0 B．  = 2x

C．(   - 1)(   - 2) = 0 D．  = 0

5．在菱形ABCD中，对角线AC与BD相交于点O，添加以下条件，能判定菱形ABCD是正方形的是（　　）

A．AB = AC B．OA = OC C．BC⊥CD D．AC⊥BD

6．把抛物线y=2x2向下平移1个单位，则平移后抛物线的解析式为（　　）

A．y=2x2 + 1 B．y=2x2-1 C．y=  D．y=

7．工人师傅在做矩形门窗时，不仅要测量两组对边的长度是否分别相等，还要测量它们的两条对角线是否相等，以确定门窗是否为矩形.这样做的依据是（　　） 

A．矩形的两组对边分别相等

B．矩形的两条对角线相等

C．有一个角是直角的平行四边形是矩形

D．对角线相等的平行四边形是矩形

8．如图，在直角坐标系中，△OAB的顶点为O(0，0)，A(4，3),B(3，0).以点O为位似中心，在第三象限内作与△OAB的位似比为 的位似图形△OCD，则点C坐标（　　）

A．(- ，-1) B．(-1，- )

C．(-1，-1) D．(-2，-1)

9．点A(m，n)在二次函数y= -4的图象上，则2M-n的最大值是（　　）

A．-5 B．-4 C．4 D．5

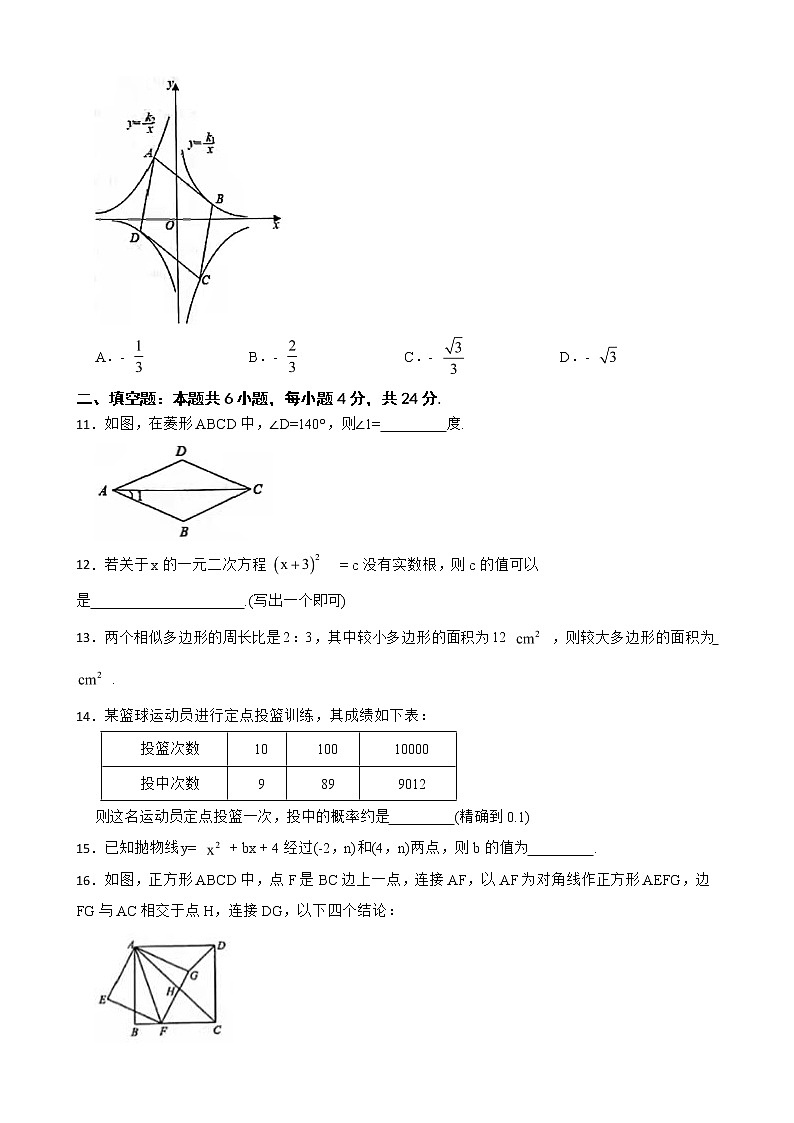
10．如图，菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上，若∠BCD=60°，则 的值是（　　）

A．-  B．-  C．-  D．-

二、填空题：本题共6小题，每小题4分，共24分.

11．如图，在菱形ABCD中，∠D=140°，则∠1=　     　度.

12．若关于x的一元二次方程   = c没有实数根，则c的值可以是　                 　.(写出一个即可)

13．两个相似多边形的周长比是2：3，其中较小多边形的面积为12 ，则较大多边形的面积为　     　 .

14．某篮球运动员进行定点投篮训练，其成绩如下表：

则这名运动员定点投篮一次，投中的概率约是　     　(精确到0.1)

15．已知抛物线y= + bx + 4经过(-2，n)和(4，n)两点，则b的值为　     　.

16．如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与AC相交于点H，连接DG，以下四个结论：

①∠EAB=∠BFE=∠DAG；

②△ACF∽△ADG；

③AH﹒AC = A ；

④DG⊥AC .

其中正确的是　     　.(写出所有正确结论的序号)

三、解答题：本题共9小题，共86分，解答应写出文字说明、证明过程或演算步骤.

17．解方程： + 4x - 5 = 0.

18．如图是两根木杆及其影子的图形.

（1）这个图形反映的是中心投影还是平行投影?答：　         　

（2）请你在图中画出表示小树影长的线段AB.

19．已知某品牌蓄电池的电压为定值，使用该蓄电池作为电源时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示.

（1）求这个反比例函数的表达式；

（2）如果以此蓄电池为电源的用电器的电流不能超过8A，那么该用电器的可变电阻至少是多少?

20．2022年冬奥会在我国北京和张家口举行，如图所示为冬奥会和冬残会的会徽“冬梦”“飞跃”，吉祥物“冰墩墩”“雪容融”，将四张正面分别印有以上4个图案的卡片(卡片的形状、大小、质地都相同)背面朝上洗匀.

（1）若从中随机抽取一张卡片，则抽取的卡片上的图案恰好为吉样物“冰墩墩”的概率是　     　；

（2）若从中一次同时随机抽取两张卡片，请用画树状图或列表的方法，求抽取的两张卡片上的图案正好一张是会徽另一张是吉祥物的概率.

21．如图，在△ABC中，D是AB边上一点，且BD=2DA.

（1）在AC边上求作点E，使CE=2EA；(要求：尺规作图，不写作法，保留作图痕迹)

（2）在(1)的条件下，若BC=12，求DE的长，

22．在菱形ABCD中，∠BAD = 60°，点E、F分别在边AB、AD上，且AE = DF，BF与DE交于点G.

（1）如图①，连接BD. 求证：△ADE ≌ △DBF；

（2）如图②，连接CG. 求证：BG + DG = CG.

23．2021年是我国脱贫胜利年，我国在扶贫方面取得了巨大的成就，技术扶贫也使得某县的一个电子器件厂扭亏为盈.该电子器件厂生产一种电脑显卡，2019年该类电脑显卡的成本是200元/个，2020年与2021年连续两年在技术扶贫的帮助下改进技术，降低成本，2021年该电脑显卡的成本降低到162元/个.

（1）若这两年此类电脑显卡成本下降的百分率相同，求平均每年下降的百分率；

（2）2021年某商场以高于成本价10%的价格购进若干个此类电脑显卡，以216.2元/个销售时，平均每天可销售20个，为了减少库存，商场决定降价销售. 经调查发现，单价每降低5元，每天可多售出10个，如果每天盈利1120元，单价应降低多少元?

24．在矩形ABCD中，AB = 6，AD = 4，点M为AB边上一个动点，连接DM，过点M作MN⊥DM，且MN =   DM，连接DN.

（1）如图①，连接BD与BN，BD交MN于点E.

①求证：△ABD∽△MND；

②求证：∠CBN=∠DNM；

（2）如图②，当AM=4BM时，求证：A，C，N三点在同一条直线上.

25．平面直角坐标系中，抛物线y = - +2ax + 1 - a(a为常数)的顶点为A.

（1）当抛物线经过点(1，2)，求抛物线的函数表达式；

（2）求顶点A的坐标(用含字母ɑ的代数式表示)，判断顶点A在x轴的上方还是下方，并说明理由；

（3）当x ≥0时，抛物线y = -   + 2ɑx + 1 - ɑ(ɑ为常数)的最高点到直线y = 3ɑ的距离为5，求ɑ的值.

答案解析部分

【解析】【解答】解：粮仓主视图上部视图为等腰三角形，下部视图为矩形．

故答案为：A．

【分析】根据所给图形粮仓和主视图的定义求解即可。

【解析】【解答】解：A、∵  = ，∴xy=12，错误；
B、∵  = ，∴4x=3y，错误；
C、∵  = ，∴3x=4y，正确；
D、∵  = ，∴4x=3y，错误.
故答案为：C.

【分析】由比例的性质可知，内项之积等于外项之积，依此分别判断，即可作答.

【解析】【解答】解：A、阴影三角形与原三角形的对应角相等、对应边的比相等，符合相似多边形的定义，正确；
B、阴影矩形与原矩形的对应角相等，但对应边不成比例，不符合相似多边形的定义，错误； 
C、阴影五边形与原五边形的对应角相等，但对应边不成比例，不符合相似多边形的定义，错误； 
D、阴影六边形与原六边形的对应角相等，但对应边不成比例，不符合相似多边形的定，错误. 
故答案为：A. 

 【分析】对应角相等，对应边成比例的两个多边形相似，根据相似多边形的定义分别判断，即可作答.

【解析】【解答】解：A、 ∵  + 2 >0，∴△=-8<0，∴无实数根，错误；
B、∵ = 2x，∴ - 2x=0，△=4>0，有两个不相等的实数根，错误；
C、∵(   - 1)(   - 2) = 0 ，∴x2-3x+2=0，∴△=9-8=1>0，有两个不相等的实数根，错误；
D、∵  = 0，∴x2-2x+1=0，∴△=4-4=0，有两个相等的实数根，正确.

故答案为：D.

【分析】一元二次方程ax2+bx+c=0(a≠0)根的判别式是△=b2-4ac，当△>0时，有两个不相等的实数根，当△=0时，有两个相等的实数根，当△<0时，没有实数根。先把原方程化为一元二次方程的一般式，再求出△值，即可判断.

【解析】【解答】解：A、∵四边形ABCD为菱形，∴AB=BC，∴AB=BC=AC，△ABC是等边三角形，∴∠ABC=60°，∴四边形ABCD不是正方形，错误；
B、∵四边形ABCD为菱形，∴OA=OC，不能判定四边形ABCD不是正方形，错误；
C、∵四边形ABCD为菱形，BC⊥CD，∴四边形ABCD不是正方形，正确；
D、∵四边形ABCD为菱形，∴AC⊥BD，不能判定四边形ABCD不是正方形，错误.
故答案为：C. 

 【分析】有一个内角等于90°的菱形是正方形，依此分别判断；而仅有菱形本身的性质不能判定是否是正方形.

【解析】【解答】解： ∵抛物线y=2x2向下平移1个单位，
∴y=2x2-1.
故答案为：B.
 

【分析】对于二次函数y=a(x+h)2+k, 根据抛物线的平移规律：即左右平移在h后左加右减，上下平移在k后上加下减即可求出结果.

【解析】【解答】解：∵两组对边相等分别相等的四边形是平行四边形，
又∵两条对角线相等，
∴该门框是矩形.
故答案为：D.
 

【分析】先利用两组对边分别相等判定该四边形是平行四边形；结合两条对角线相等，则可判定该门框是矩形.

【解析】【解答】解：∵△OAB和△OCD以原点O为位似中心，位似比为 ，且点C在第三象限，
A点坐标为（4,3），
又A点的对应点为C点，
∴点C的坐标为（-4× ，-3× ），即 (- ，-1) .
故答案为：A.

【分析】根据关于以原点为位似中心的对应点的坐标的关系，把A点的横纵坐标都乘以 ，结合C点所在的象限，即可求解

【解析】【解答】解：由题意得：n=m2-4，
∴2m-n=2m-m2+4=-(m-2)2+5，
当m=2时，2m-n有最大值5. 
故答案为：D. 
 

【分析】把A点坐标代入函数式得出n=m2-4，将此代入原式，再化成顶点式，根据二次函数的性质求最大值即可.

【解析】【解答】解：如图，连接AC、BD，作BM⊥x轴于M，CN⊥x轴于N，

∵ 四边形ABCD是菱形，
∴AC⊥BD，
∴ 菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上，
∴ A与C、B与D关于原点对称，
∴ AC、BD经过点O，
∴∠BOC=90°，
∴∠BCO= ∠BCD=30°，
∴tan30°= = ，
∵∠BOM+∠NOC=90°，∠NOC+∠NCO=90°，
∴∠BOM=∠NCO，
∴∠OMB=∠CNO= 90°，
∴ △OMB∽△CNO，
∴，

∴，
∵k1>0，k2<0，
即
故答案为：A.

【分析】连接AC、BD，作BM⊥x轴于M，CN⊥x轴于N，根据菱形的性质和反比例函数图象的对称性得出∠BOC=90°, ∠BCO= ∠BCD=30°，然后根据正切三角函数定义求得tan30°= = ，再证明△OMB∽△CNO，根据相似三角形的性质得出 ，结合反比例函数系数k的几何意义即可求得结果.

【解析】【解答】解：∵四边形ABCD是菱形，
∴∠1=∠CAD= ∠BAD，AB∥CD，
∵∠D=140°，
∴∠BAD=180°-∠D=40°，
∴∠1=20°.
故答案为：20.
 

【分析】由菱形的性质得出∠1= ∠BAD，AB∥CD，然后由平行线的性质求出∠BAD，则可求出∠1的度数.

【解析】【解答】解：∵一元二次方程    = c没有实数根，

∵≥0，
∴c<0，该方程没有实数根，
∴c可取-1.
故答案为：-1（答案不唯一）.

【分析】根据完全平方式的非负性得出：当c<0，该方程没有实数根，则在其范围内任意一个负数即可.

【解析】【解答】解：设较大多边形的面积为x，
∵两个多边形相似，周长比为2：3，
∴面积比=4：9，
∴12：x=4：9，
解得x=27.
故答案为：27.

 【分析】设较大多边形的面积为x，根据相似多边形的周长比等于相似比，而面积比等于相似比的平方，建立关于x的方程求解即可.

【解析】【解答】解：∵，
∴这名运动员定点投篮一次，投中的概率约是0.9.
故答案为：0.9.
 

【分析】对于不同批次的定点投篮命中率往往误差会较大，为了减少误差，则常采用多批次计算求平均数的方法来确定投中的概率.

【解析】【解答】解：由题意得：对称轴x= =1，
∴- =1，
解得b=-2.
故答案为：-2.

【分析】由于已知两点的纵坐标相等，根据中点坐标公式求出对称轴方程，然后根据抛物线对称轴公式列方程求解即可.

【解析】【解答】解：①如图，取AB和EF的交点为O，

∵四边形4EFG和四边形ABCD均为正方形，
∴∠EAG=∠BAD= 90°，
又∵∠EAB= 90°-BAG，
∠GAD = 90°-∠BAG，
∴∠EAB=∠GAD，
∵∠AOE=∠BOF，∠AEO=∠FBO=90°，
∴∠EAB=∠BFE，
∴∠EAB=∠BFE=∠DAG，故①正确；

②∵四边形AEFG和四边形ABCD均为正方形,
∴AD=DC，AG= FG，
∴AC= AD，AF= AG，
∴= ， = ，
∴，
又∵∠DAG+∠GAC=∠FAC+∠GAC=45°，
∴∠DAG=∠CAF，
∴△ACF∽△ADG，故②正确；
③∵四边形AEFG和四边形ABCD均为正方形，AF、AC为对角线，
∴∠AFH= CACF=45°,
又∵∠FAH=∠CAF，
∴△HAF∽△FAC，
∴，
即AF2 =AC·AH，
又∵AF= AE，
∴AH·AC=2AE2 ，故③错误；
④由②知△ACF∽△ADG，
∵四边形ABCD为正方形, AC为对角线，
∴∠ADG=∠ACF =45°，
∴DG在正方形另外一条对角线上，
∴DG⊥AC，故④正确，
综上，正确的个数为 ①②④ .
故答案为： ①②④ .​​​​​

【分析】①正方形的性质得到∠EAG=∠BAD=90°，根据余角的性质得出∠EAB =∠GAD；②根据正方形的对角线等于边长的 倍，得到两组对边对应成比例，再求出∠DAG=∠CAF，则可判定 △ACF∽△ADG；③先证明△HAF∽△FAC，利用相似三角形的性质列比例式得到AF2 =AC·AH，结合AF= AE，推出AH·AC=2AE2 ，即可作出判断；④由②知△ACF∽△ADG，得出∠ADG=∠ACF=45°,得出DG在正方形ABCD对角线BD上，根据正方形对角线互相垂直即可判断.

【解析】【分析】先移项，将右式化为0，然后两边同时加4，将左式配成完全平方式，再两边同时开方，即可求解.

【解析】【分析】(1) 平行投影与中心投影之间的区别是：平行投影与原物体所对应点的连线都相互平行，而中心投影与原物体所对应点的连线都相交于一点。结合两个木杆及其影子的图形即可判断.
(2)利用中心投影的性质画图，连接投影中心和小树顶点的连线，得出顶端投影点，将其和树的底端连接起来即可.

【解析】【分析】(1) 设反比例函数表达式为I＝   （k≠0） ，结合已知点坐标，利用待定系数法求反比例函数式即可；
(2)把I=8代入函数式求出R值，由反比例函数的性质可知，由于k>0， I随着R的增大而减小 ，则可求出R的范围，则可解答.

【解析】【解答】解：(1)解： ∵从中任意抽取1张有4种可能的结果，抽得卡片上的图案恰好为“冰墩墩’有1种可能的结果，
∴抽得卡片上的图案恰好为“冰墩墩”的概率= .
故答案为： .

【分析】(1)根据题意求出任意抽取1张和抽得卡片上的图案恰好为“冰墩墩”的结果数，依此求概率即可；
(2)根据题意画出树状图，列出所有的等可能出现的结果数，找出其中两张卡片上的图案正好一张是会徽另一张是吉祥物的可能的结果数，然后计算概率即可.

【解析】【分析】(1)过D点作∠ADE等于∠ABC，DE交AC于E点，根据平行线分线段成比例的性质得出 CE=2EA；
(2)由(1)得出 ，结合∠BAC＝∠DAE，证明 △ADE∽△ABC， 根据相似三角形的性质列比例式建立关于DE的方程，即可解答.

【解析】【分析】(1)根据菱形的性质，结合∠BAD=60°，求出△ABD为等边三角形，则得AB=BD， ∠BDF＝∠DAE，然后利用SAS证明△ADE∽△DBF即可；
(2)①延长GB到点H，使BH＝DG，连结CH、BD，由（1）知△ADE≌△DBF，△CBD是等边三角形 ，求出 ∠DBF+∠CBH＝ 120° ，结合 ∠ADE+∠CDG＝120° ，则可得出 ∠CBH＝∠CDG ，然后利用SAS证明△CBH≌△CDG ，得出CH＝CG，∠BCH＝∠DCG， 求出∠BCD=60°，证出 △CGH是等边三角形， 得出GH=CG，最后根据线段间的和差关系即可证出结果.

【解析】【分析】(1)设平均每年下降百分率为x，根据“原成本为200元/个，经过连续两年的降本，成本下降到162元/个”，建立关于x的方程求解即可；
(2) 设单价应降低m元， 先把每个销售利润和每天的销售量分别用含m的代数式表示，然后根据“单件销售利润×每天销售量=每天盈利”，建立关于m的方程求解，结合减少库存的要求，即可确定m值.

【解析】【分析】(1) ① 根据矩形的性质和垂直的定义求出∠A=∠DMN，再根据已知线段的长，求出 ，则可判定 △ABD∽△MND ；
②由①得△ABD∽△MND ，得出 ∠ABD＝∠DNM ，然后证明△MBE∽△DNE， 得出 ，再证明△DME∽△NBE ，得出 ∠NBE＝∠DME=90° ，最后根据余角的性质即可证出 ∠CBN＝∠DNM ；
(2) 过点N作NF⊥AB，交AB延长线于点F，连接AC，AN，根据线段的长求出， 由余角的性质得出∠ADM＝∠FMN ，则可证明△ADM∽△FMN ，列比例式求出MF和FN长，求出  ，则可得出 ，结合 ∠ABC＝∠AFN＝90° ，证明△ABC∽△AFN，得出∠BAC＝∠FAN，即可证明A，C，N三点在同一条直线上.
 

【解析】【分析】(1)利用待定系数法求二次函数表达式即可；
(2)先把抛物线的解析式化成顶点式，则可把顶点的坐标表示出来，然后配方法或一元二次方程根的判别式判断顶点纵坐标的符号，则可判断A在x轴的上方还是下方；
(3)先求出对称轴和顶点坐标，然后分两种情况讨论，①当a＜0时，对称轴在y轴左侧， 结合x≥0 ，得出最高点坐标为 （0，1－a）；②当a＞0，对称轴在y轴右侧， 结合x≥0 ，得出最高点坐标为 （a，a2－a+1） ，然后根据图象的最高点到直线y＝3a的距离为5，分别建立关于a的方程求解即可.