北师大数学七下复习阶梯训练：三角形（优生加练）含解析

这是一份北师大数学七下复习阶梯训练：三角形（优生加练）含解析，共24页。试卷主要包含了单选题，填空题，解答题，综合题等内容，欢迎下载使用。
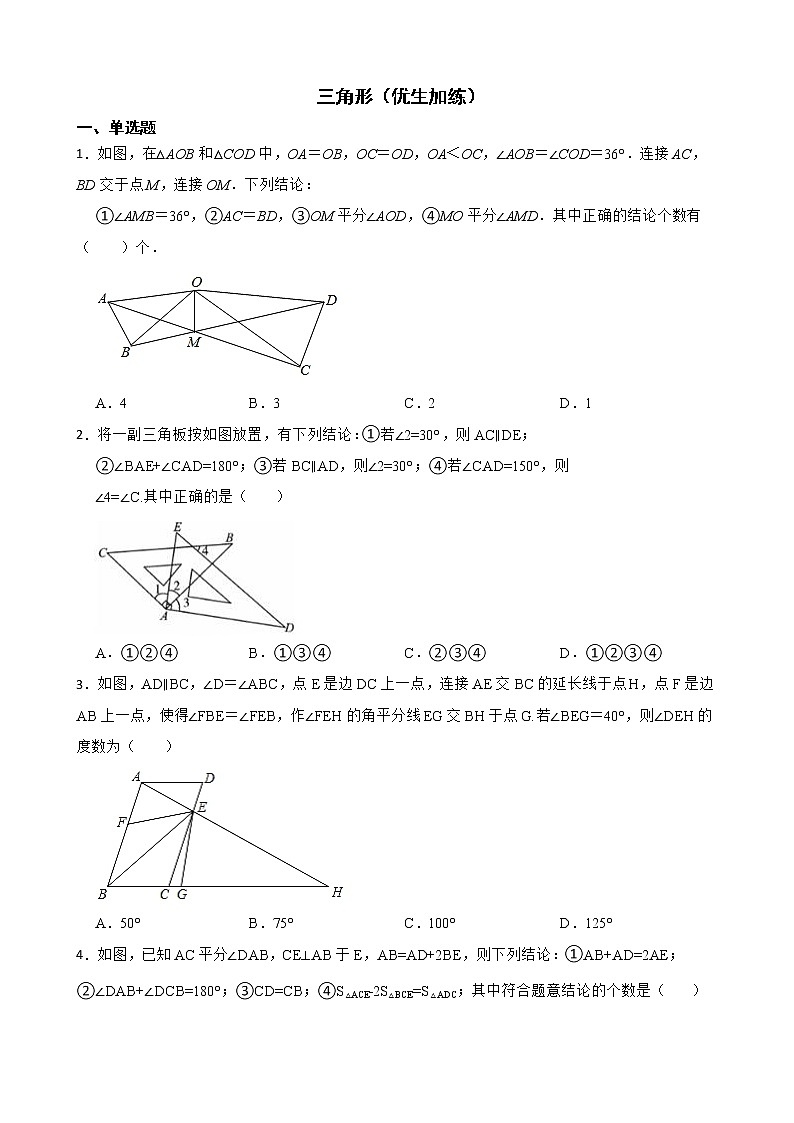
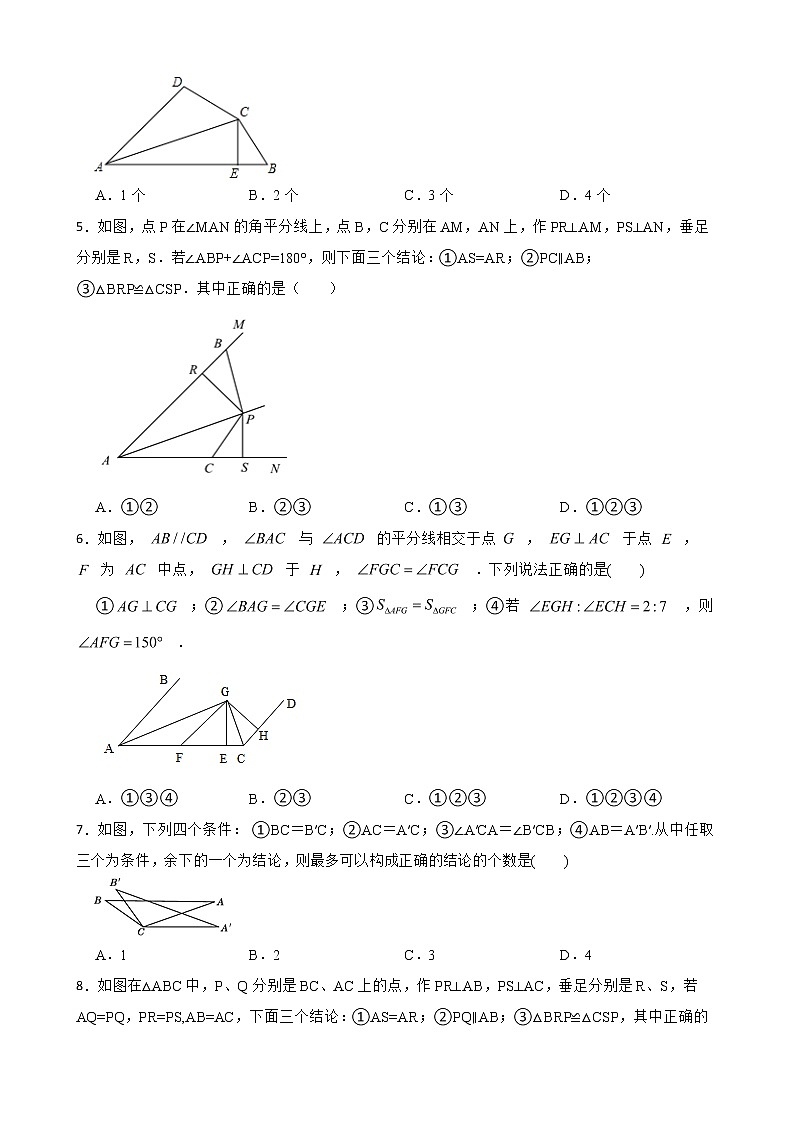
 三角形（优生加练）一、单选题1．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°．连接AC，BD交于点M，连接OM．下列结论：  ①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO平分∠AMD．其中正确的结论个数有（　　）个．A．4 B．3 C．2 D．12．将一副三角板按如图放置，有下列结论：①若∠2=30°，则AC∥DE；  ②∠BAE+∠CAD=180°；③若BC∥AD，则∠2=30°；④若∠CAD=150°，则∠4=∠C.其中正确的是（　　）A．①②④ B．①③④ C．②③④ D．①②③④3．如图，AD∥BC，∠D＝∠ABC，点E是边DC上一点，连接AE交BC的延长线于点H，点F是边AB上一点，使得∠FBE＝∠FEB，作∠FEH的角平分线EG交BH于点G.若∠BEG＝40°，则∠DEH的度数为（　　）  A．50° B．75° C．100° D．125°4．如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE﹣2S△BCE=S△ADC；其中符合题意结论的个数是（　　）     A．1个 B．2个 C．3个 D．4个5．如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（　　）  A．①② B．②③ C．①③ D．①②③6．如图， ， 与 的平分线相交于点 ， 于点 ， 为 中点， 于 ， ．下列说法正确的是(　　)  ① ；② ；③ ；④若 ，则 ．A．①③④ B．②③ C．①②③ D．①②③④7．如图，下列四个条件： ①BC＝B′C；②AC＝A′C；③∠A′CA＝∠B′CB；④AB＝A′B′.从中任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是(　　)  A．1 B．2 C．3 D．48．如图在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS,AB=AC，下面三个结论：①AS=AR；②PQ∥AB；③△BRP≌△CSP，其中正确的是（　　）A．①② B．②③ C．①③ D．①②③9．如图，是三个等边三角形（注：等边三角形的三个内角都相等）随意摆放的图形，则 等于（　　）A．90° B．120° C．150° D．180°10．在下列四组条件中，能判定△ABC≌△DEF的是（　　）A．AB=DE  ， BC= EF  ， ∠A=∠D       B．∠A=∠D  ， ∠C=∠F  ， AC= DEC．∠A=∠E  ， ∠B=∠F  ， ∠C=∠D D．AB=DE  ， BC= EF  ， △ABC的周长等于△DEF的周长二、填空题11．如图，己知 ，点 在 上，点 为平面内一点， ，过点 作 平分 平分 ，若 ，则 　     　.12．如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成，在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行．当∠EFH=55°，BC∥EF时，∠ABC=　     　度；如图3，为了参与另外一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF所在直线互相垂直，且∠EFH=78°，则这时∠ABC=　     　 度 13．如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA＝ BC，EB＝AC，FC＝AB，∠AFB＝50°，则∠DFE＝　     　．14．如图，△DAC和△EBC均是等边三角形，A、C、B三点共线，AE与BD相交于点P，AE与BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②∠DPA＝60°；③AC＝DN；④EM＝BN；⑤DC∥EB，其中正确结论是　         　（填序号）15．如图，在四边形 中， ， ， 于点 ， 于点 ， 、 分别是 、 上的点，且 ，下列说法正确的是　     　.（填写正确的序号）  ① ，② ，③ 平分 ，④ 平分 ，⑤ ，⑥ .16．如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，其中点C，D，E在同一条直线上，连接BD，BE。以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC正确的是　     　三、解答题17．如图，在 和 中，点 、 、 、 在同一直线上，请你从以下4个等式中选出3个作为已知条件，余下的1个作为结论，并说明结论正确的理由（写出各种可能的情况，并选择其中一种说理）．  ① ；② ；③ ；④ ．18．如图，已知△ABC≌△ADE，AB与ED交于点M，BC与ED，AD分别交于点F，N.请写出图中两对全等三角形(△ABC≌△ADE除外)，并选择其中的一对加以说明．19．如图，已知DA⊥AB，DE平分∠ADC，CE平分 ∠BCD， ∠1+ ∠2=90°．求证：BC ⊥ AB．
 20．如图所示，在 △ ABC中， ∠ABC=∠C，BD⊥AC交AC于D．求证： ∠DBC= ∠A．               
 21．如图，求 ∠A+∠B+∠C+∠D+∠E的大小．
 22．如图，AB、CD相交于E，CF、BF分别为 ∠ACD和 ∠ABD的平分线，它们相交于F．求证：∠F= ( A+D)．四、综合题23．如图，已知点E，F在直线AB上，点 在线段CD上，ED与FG交于点  .  （1）求证: .（2）试判断 与  之间的数量关系，并说明理由.（3）若 ，求  的度数.24．如图，在同一平面内，点D、E是△ABC外的两点，请按要求完成下列问题．（此题作图不要求写出画法）（1）请你判断线段与AC的数量关系是　          　，理由是　                               　．（2）连接线段CD，作射线BE、直线DE，在四边形BCDE的边BC、CD、DE、EB上任取一点，分别为点K、L、M、N并顺次连接它们，则四边形KLMN的周长与四边形BCDE周长哪一个大，直接写出结果（不用说出理由）．（3）在四边形KLMN内找一点O，使它到四边形四个顶点的距离之和最小（作图找到点即可）．25．如图所示，已知射线CB∥OA，∠C=∠OAB=100°，E，F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．（1）求∠EOB的度数；(直接写出结果)（2）若在0C右侧左右平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，请找出变化的规律；若不变，请求出这个比值；（3）在OC右侧左右平行移动AB的过程中，是否存在使∠OEC=∠OBA的情况？若存在，请直接写出∠OEC的度数；若不存在，请说明理由．26．已知CD是经过∠BCA顶点C的一条直线，CA=CB．E、F分别是直线CD上两点，且∠BEC=∠CFA=∠ ．  （1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：①如图1若∠BCA=90°，∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.②如图2，若0°＜∠BCA＜180°， 请添加一个关于∠ 与∠BCA关系的条件，使①中的结论仍然成立；（2）如图3，若直线CD经过∠BCA的外部，∠ =∠BCA，请写出三条线段EF、BE、AF的数量关系并证明你的结论. 
答案解析部分【解析】【解答】解：∵∠AOB＝∠COD＝36°，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠BOD，在△AOC和△BOD中，∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②符合题意；∵∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OBD＝∠OAC+∠AOB，∴∠AMB＝∠AOB＝36°，故①符合题意；作OG⊥AM于G，OH⊥DM于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，所以两个三角形的面积相等，∵AC＝BD，∴OG＝OH，∴MO平分∠AMD，故④符合题意；假设MO平分∠AOD，则∠DOM＝∠AOM，在△AMO与△DMO中， ，∴△AMO≌△DMO（ASA），∴AO＝OD，∵OC＝OD，∴OA＝OC，而OA＜OC，故③不符合题意；正确的个数有3个；故答案为：B．
【分析】由SAS证明△AOC≌△BOD得出∠OCA＝∠ODB，AC＝BD，故②符合题意；由全等三角形的性质得出∠OAC＝∠OBD，由∠AMB+∠OBD＝∠OAC+∠AOB，得出∠AMB＝∠AOB＝36°，故①符合题意；作OG⊥AM于G，OH⊥DM于H，利用全等三角形对应边上的高相等，得出OG＝OH，由角平分线的判定方法得出MO平分∠AMD，故④符合题意；假设MO平分∠AOD，则∠DOM＝∠AOM，由全等三角形的判定定理可得△AMO≌△DMO，得出AO＝OD，而OC＝OD，所以OA＝OC，而OA＜OC，故③不符合题意；即可得出结论。【解析】【解答】解：∵∠2=30°，∠CAB=90°
∴∠1=60°
∵∠E=60°
∴∠1=∠E
∴AC∥DE，即①正确；
∵∠CAB=∠DAE=90°
∴∠BAE+∠CAD=90°-∠1+90°+∠1=180°，即②正确；
∵BC∥AD，∠B=45°
∴∠3=∠B=45°
∵∠2+∠3=∠DAE=90°
∴∠2=45°，即③错误
∵∠CAD=150°，∠BAE+∠CAD=180°
∴∠BAE=30°
∵∠E=60°
∴∠BOE=∠BAE+∠E=90°
∴∠4+∠B=90°
∵∠B=45°
∴∠4=45°
∵∠C=45°
∴∠4=∠C，即④正确故答案为：A.
【分析】根据平行线的性质和判定、三角形的内角和定理逐个判断得到答案即可。【解析】【解答】解：设∠FBE＝∠FEB＝α，则∠AFE＝2α，∠FEH的角平分线为EG，设∠GEH＝∠GEF＝β，∵AD∥BC，∴∠ABC+∠BAD＝180°，∵∠D＝∠ABC，∴∠D+∠BAD＝180°，∴AB∥CD，∵∠BEG＝40°，∴∠BEG＝∠FEG﹣∠FEB＝β﹣α＝40°，∵∠AEF＝180°﹣∠FEG﹣∠HEG＝180°﹣2β，在△AEF中，180°﹣2β+2α+∠FAE＝180°，∴∠FAE＝2β﹣2α＝2（β﹣α）＝80°，∵AB∥CD，∴∠CEH＝∠FAE＝80°，∴∠DEH＝180°﹣∠CEH＝100°.故答案为：C.【分析】设∠FBE＝∠FEB＝α，则∠AFE＝2α，设∠GEH＝∠GEF＝β，由二直线平行，同旁内角互补可得∠ABC+∠BAD＝180°，结合已知条件可得∠D+∠BAD＝180°，推出AB∥CD，求出∠BEG的度数，由平角的概念可得∠AEF＝180°-2β，在△AEF中，由三角形内角和定理可得∠FAE＝80°，然后由平行线的性质可得∠CEH＝∠FAE＝80°，最后根据平角的概念进行求解.【解析】【解答】解：①在AE取点F，使EF=BE，∵AB=AD+2BE=AF+EF+BE，EF=BE，∴AB=AD+2BE=AF+2BE，∴AD=AF，∴AB+AD=AF+EF+BE+AD=2AF+2EF=2（AF+EF）=2AE，∴AE= （AB+AD），故①符合题意；②在AB上取点F，使BE=EF，连接CF．在△ACD与△ACF中，∵AD=AF，∠DAC=∠FAC，AC=AC，∴△ACD≌△ACF，∴∠ADC=∠AFC．∵CE垂直平分BF，∴CF=CB，∴∠CFB=∠B．又∵∠AFC+∠CFB=180°，∴∠ADC+∠B=180°，∴∠DAB+∠DCB=360-（∠ADC+∠B）=180°，故②符合题意；③由②知，△ACD≌△ACF，∴CD=CF，又∵CF=CB，∴CD=CB，故③符合题意；④易证△CEF≌△CEB，所以S△ACE-S△BCE=S△ACE-S△FCE=S△ACF，又∵△ACD≌△ACF，∴S△ACF=S△ADC，∴S△ACE-S△BCE=S△ADC，故④不符合题意；即正确的有3个，故答案为：C．【分析】①在AE取点F，使EF=BE．利用已知条件AB=AD+2BE，可得AD=AF，进而证出2AE=AB+AD；②在AB上取点F，使BE=EF，连接CF．先由SAS证明△ACD≌△ACF，得出∠ADC=∠AFC；再根据线段垂直平分线、等腰三角形的性质得出∠CFB=∠B；然后由邻补角定义及四边形的内角和定理得出∠DAB+∠DCB=180°；③根据全等三角形的对应边相等得出CD=CF，根据线段垂直平分线的性质得出CF=CB，从而CD=CB；④由于△CEF≌△CEB，△ACD≌△ACF，根据全等三角形的面积相等易证S△ACE-S△BCE=S△ADC．【解析】【解答】解：∵点 P 在∠MAN的角平分上，PR⊥AM， PS⊥AN，∴PR=PS，∵∠ARP=∠ASP=90°，∴在Rt△APR和Rt△APS中， ，∴△APR≌△APS（HL），∴AS=AR，故①符合题意；∵∠ABP +∠ACP = 180°，∴∠ABP=∠PCS，又∵PR=PS，∠PRB=∠PSC=90°，∴△BRP≌△CSP（AAS），故③符合题意；若∠MAP=∠CPA，则PC∥AB，则需要AC=PC得出∠PAN=∠CPA，从而根据∠MAP=∠PAN，得出∠MAP=∠CPA，而题中没有条件说明AC=PC，故②不符合题意；故答案为：C．【分析】利用角平分线的性质得到PR=PS，再利用HL证明△APR≌△APS，得到AS=AR，可判断①；再根据∠ABP +∠ACP = 180°，得到∠ABP=∠PCS，再利用AAS证明△BRP≌△CSP可判断③；再说明若要PC∥AB，则需要说明AC=PC，无法达成，从而可判断②.【解析】【解答】①中，∵AB∥CD，∴ ，∵∠BAC与∠DCA的平分线相交于点G，∴ ，∵ ，∴∴AG⊥CG，则①符合题意；②中，由①得AG⊥CG，∵ ， ，∴根据等角的余角相等得 ，∵AG平分 ，∴ ，∴ ，则②符合题意；③中，根据三角形的面积公式，∵ 为 中点，∴AF=CF，∵ 与 等底等高，∴ ，则③符合题意；④中，根据题意，得：在四边形GECH中， ，又∵ ，∴ ，∵CG平分∠ECH，∴ ，根据直角三角形的两个锐角互余，得 .∵ ，∴ ，∴ ，∵ ，∴ ，∴ ，则④不符合题意.故正确的有①②③，故答案为：C．【分析】根据平行线的性质以及角平分线的定义即可得到 从而根据三角形的内角和定理得到 ，即可判断①符合题意性；根据等角的余角相等可知 ，再由角平分线的定义与等量代换可知 ，即可判断②符合题意性；通过面积的计算方法，由等底等高的三角形面积相等，即可判断③符合题意性；通过角度的和差计算先求出 的度数，再求出 ，再由三角形内角和定理及补角关系即可判断④是否符合题意．【解析】【解答】解：Ⅰ.条件：①②③，结论：④；
∵ ∠A′CA＝∠B′CB ，
∴∠A′CA+∠ACB′＝∠B′CB+∠ACB′ ，
即∠A′CB′＝∠ACB ，
∵B′C =BC，A′C=AC；，
∴△A′CB′≌△ACB（SAS），
∴ A′B′＝AB.
即条件：①②③，结论：④正确；
Ⅱ.条件：①②④，结论：③；
∵ BC＝B′C，AC＝A′C ，AB＝A′B′.，
∴△ACB≌△A′CB′（SSS），
∴∠A′CB′＝∠ACB ，
∴∠A′CB′-∠ACB′＝∠ACB-∠ACB′ ，
即∠A′CA＝∠B′CB .
即条件：①②④，结论：③正确；
Ⅲ.条件②③④，SSA不能证明三角形全等，故不能得出结论①.
Ⅳ.条件①③④，SSA不能证明三角形全等，故不能得出结论②.
综上所述：最多可以构成正确的结论个数为：2个.
故答案为：B.
【分析】根据全等三角形的判定逐一分析即可得出答案.【解析】【解答】解：连接AP在Rt△ASP和Rt△ARP中PR=PS，PA=PA∴Rt△ASP≌Rt△ARP∴①AS=AR正确∵AQ=PQ∴∠QAP=∠QPA又∵Rt△ASP≌Rt△ARP∴∠PAR=∠PAQ于是∠RAP=∠QPA∴②PQ∥AR正确③由AB=AC，AS=AR∴BR=CS,又∵PR=PS，∠BRP=∠CSP, ∴△BRP≌△CSP，故填①②③。故选：D【分析】本题主要考查角平分线的判定、平行四边形的判定及三角形全等的判定；准确作出辅助线是解决本题的关键，做题时要注意添加适当的辅助线，是十分重要的，要掌握.【解析】【解答】∵图中是三个等边三角形，∴∠1=180°﹣60°﹣∠ABC=120°﹣∠ABC，∠2=180°﹣60°﹣∠ACB=120°﹣∠ACB，∠3=180°﹣60°﹣∠BAC=120°﹣∠BAC，∵∠ABC+∠ACB+∠BAC=180°，∴∠1+∠2+∠3=360°﹣180°=180°，故答案为：D．【分析】根据等边三角形的内角为60°和平角为180°，可得∠1=180°-60°-∠ABC，同理可得∠2、∠3的式子，而在三角形ABC中，∠ABC+∠ACB+∠BAC=180°，化解即可求出∠1+∠2+∠3的和.【解析】【解答】A中不是夹角相等；B中不是夹边相等；C中没有至少一条边；
故答案为：D。
【分析】此题综合考查了三角形全等的判定方法，把常常出错的地方都进行了强化训练，是一道不错的综合性质题目．【解析】【解答】解：设 平分 ， 平分 在 中 ， 即 解得 故答案为： 【分析】设，可求出，，从而得出，利用三角形内角和求出∠ABC=180°-∠CAB-∠ACB=，根据补角的性质可得，据此建立方程求出α，由于=2α，从而得出结论.【解析】【解答】解：如图，过点B作BK∥EH，

∵BC∥EF，BK∥EH，
∴∠CBK=∠EFH=55°，
∴∠ABC=180°-∠CBK=125°；
如图，延长EF、BC交于点G，再延长AB与EF的延长线交于点K，

∵延展臂BC与支撑臂EF所在直线互相垂直，
∴BG⊥FK，
∵AK∥FH，
∴∠K=∠EFH=78°，
∴∠GBK=90°-∠K=12°，
∴∠ABC=180°-12°=168°，
故答案为：125；168.
【分析】在图2中过点B作BK∥EH，由平行线的性质可得∠CBK=∠EFH，再计算补角即可求解；在图3中，延长EF、BC交于点G，再延长AB与EF的延长线交于点K，由平行线的性质得出∠K=∠EFH，再根据三角形内角和定理求出∠GBK，再计算补角即可求解.【解析】【解答】如图，连接BD、AE， ， ，在 和 中， ， ， ， ， ， ，即 ， 是等腰直角三角形， ，即 ，同理可得： ，即 ， ，又 ， ，解得 ，故答案为： ．【分析】先根据三角形全等的判定定理与性质可得 ，再根据角的和差、直角三角形的性质可得 ，然后根据等腰直角三角形的判定与性质可得 ，同理可得出 ，最后根据角的和差即可得．【解析】【解答】解：∵△DAC和△EBC都是等边三角形，∴∠ACD=∠BCE=60°，∴∠ACE=∠DCB=120°，在△ACE与△DCB中，∴△ACE≌△DCB（SAS），故①符合题意；在△DMP和△ACM中∵△ACE≌△DCB，∴∠BDC=∠EAC又∠DMP=∠AMC∴∠DPA=∠DCA=60°，故②符合题意；∵△ACE≌△DCB，∴∠BDC=∠EAC又∠ACD=∠BCE=60°，AC=CD在△ACM和△DCN中∴△ACM≌△DCN（ASA）∴AM=DN又根据三角形外角性质得到∠AMC＞∠MCE，则∠AMC＞∠ACM，∴AC＞AM∴AC＞DN，故③不符合题意；由②中△ACM≌△DCN可得AM=DN又△ACE≌△DCB∴AE=DB∴EM=BN，故④符合题意；∵△DAC和△EBC均是等边三角形，∴∠ACD=∠BCE=60°，∴∠DCE=60°，∴∠DCE=∠BEC，∴CD∥BE，故⑤符合题意．故答案为：①②④⑤【分析】①根据等边三角形的性质可得AC=CD，BC=CE，∠ACD=∠BCE=60°，然后求出∠ACE=∠BCD，利用“边角边”证明△ACE和△DCB全等；②通过△ACE和△DCB全等，可得到∠BDC=∠EAC，在△DMP和△ACM中，利用“8”字型可求得∠DPA=∠DCA=60°；③根据三角形外角性质得到∠AMC＞∠MCE，则∠AMC＞∠ACM，所以AC＞AM，又可证得△ACM和△DCN全等，得到AM=DN，从而得到AC＞DN；④根据全等三角形对应边相等可得AM=DN，CM=CN，然后求出EM=BN；⑤△DAC和△EBC均是等边三角形，所以∠ACD=∠BCE=60°，可得到∠DCE=60°，所以∠DCE=∠BEC，再根据内错角相等，两直线平行可得CD∥BE．【解析】【解答】解：延长EB到G，使BG=DF，连接AG，∵AB⊥CB，AD⊥CD，∴∠D=∠ABG=90°，在△ADF和△ABG中，∵AD＝AB，∠D＝∠ABG，DF＝BG，∴△ADF≌△ABG（SAS），∴AF=AG，∠G=∠DFA，∠DAF=∠BAG，∵∠EAF=70°，∠DAB=140°，∴∠DAF+∠EAB=∠DAB－∠FAE=140°－70°=70°，∴∠EAG=∠EAB+∠BAG=∠EAB+∠DAF=70°，∴∠FAE=∠EAG=70°，在△FAE和△GAE中∵AE＝AE，∠FAE＝∠EAG，AF＝AG，∴△FAE≌△GAE（SAS），∴∠FEA=∠GEA，∠G=∠EFA，EF=EG，∴EF=EB+BG= EB+DF，∠FAE≠∠EAB，故⑤正确，④错误；∴∠G=∠EFA=∠DFA，即AF平分∠DFE，故③正确；∵CF+CE＞EF，EF=DF+BE，∴CF+CE＞DF+BE，故⑥正确；根据已知不能推出△ADF≌△ABE，故②错误，①错误；故答案为：③⑤⑥.【分析】延长EB到G，使BG=DF，连接AG，利用SAS证明△ADF≌△ABG，则可得出AF=AG，∠G=∠DFA，∠DAF=∠BAG，则由角的和差关系求出∠FAE=∠EAG=70°，然后利用SAS证明△FAE≌△GAE，则可得出∠FEA=∠GEA，∠G=∠EFA，EF=EG，结合线段间的和差关系和三角形的三边关系分别进行判断，即可解答.【解析】【解答】①根据SAS定理，可判断出△BAD≌△CAE（SAS），判断出BD=CE，结论正确
②△BAD≌△CAE，可得出∠ABD=∠ACE，∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°，所以BD⊥CE，结论正确
③△ABC为等腰直角三角形，∠ABD=∠ACE，∠ACE+∠DBC=45°，结论正确
④因为∠ABC=∠ACE，所以只有当∠ABD=∠DBC时，结论才成立。
综上，正确的为①②③【分析】根据全等三角形的判定定理和性质，可进行判断。【解析】【分析】此题答案不唯一，可选择已知条件是①，②，④，结论是③．由④可得BC=EF，根据SSS可得出△ABC≌△DEF，从而证出结论③．【解析】【分析】 △AEM≌△ACN，△BMF≌△DNF，△ABN≌△ADM；△AEM≌△ACN 的理由如下：根据全等三角形的性质得 AC＝AE，∠C＝∠E，∠CAB＝∠EAD ，由全等三角形的判定ASA即可得△AEM≌△ACN.
 【解析】【分析】根据角平分线性质得∠1=∠ADE，∠2=∠BCE，结合已知条件等量代换可得∠1+∠2=∠ADE+∠BCE=90°，根据三角形内角和定理和邻补角定义可得∠BEC=∠ADE，代入前面式子即可得∠BEC+∠BCE=90°，由三角形内角和定理得∠B=90°，即BC⊥AB．【解析】【分析】在△ABC中，根据三角形内角和定理结合已知条件得∠ ABC= ∠ C=90°-∠A，再△DBC中，根据垂直定义知∠BDC=90°，由三角形内角和定理可知∠DBC+∠C=90°，两式联立计算即可得证.【解析】【分析】连结BC，根据三角形的内角和定理可得∠E+∠D+∠EFD=∠1+∠2+∠BFC=180°，由对顶角相等可得∠E+∠D=∠1+∠2，从而将∠E、∠D转化到同一个三角形中，根据三角形的内角和定理即可得出答案.【解析】【分析】根据角平分线定义得∠1=∠2，∠3=∠4，再由三角形内角和定理得∠1+∠A=∠3+∠F，①∠A+2∠1=∠D+2∠3，②联立即可得证.【解析】【分析】（1）根据同位角相等，两直线平行可直接判定；（2）∠AED+∠D=180°. 由（1）已证CE//GF得∠C=∠FGD，结合∠C=∠EFG，进而得∠FGD=∠EFG，即可证明AB//CD，再根据平行线性质即可得出结论；
（3）结合已知条件，先根据三角形内角和定理求得∠FGD=70°，由CE//GF得∠C=∠FGD=70°，再由AB//CD，可得∠AEC=∠C=70°，最后由互补关系，即∠AEM=180°-∠AEC计算即可求出.【解析】【解答】解：（1）AB+BC＞AC（三角形的两边之和之和大于第三边），故答案为：AB+BC＞AC，三角形的两边之和之和大于第三边；
【分析】（1）根据三角形的两边之和大于第三边判断即可；
（2）根据直线、射线、线段的大于以及题目要求做出图形即可；
（3）连接NL，MK，交于点O，点O即为所求。【解析】【解答】解：（1）∵CB∥OA，
∴∠C+∠COA=180°，
∴∠COA=180°-100°=80°；
∵OE平分∠COF，∠FOB=∠AOB，
∴∠EOF=∠COF，∠FOB=∠AOF，
∴∠EOB=∠EOF+∠FOB=∠COA=×80°=40°.
【分析】（1）利用两直线平行，同旁内角互补，可求出∠COA的度数；利用角平分线的定义可证得∠EOF=∠COF，∠FOB=∠AOF，由此可推出∠EOB=∠COA，代入计算可求解.
（2）利用已知条件可得到 ∠AOB= ∠FOA，利用平行线的性质可推出∠OBC=∠AOB，∠OFC=∠FOA， 然后求出∠OBC：∠OFC的值.
（3）利用三角形的内角和定理可知∠COE＝∠AOB；利用角平分线的定义和已知条件可证得OB、OE、OF是∠AOC的四等分线，由此可求出∠COE的度数；然后利用三角形的内角和定理可知∠OEC＝180°−∠C−∠COE，代入计算求出∠OEC的度数.【解析】【分析】（1）①求出∠BEC=∠AFC=90°，∠CBE=∠ACF，根据AAS证得△BCE≌△CAF，推出BE=CF，CE=AF，即可得出结论；②求出∠CBE=∠ACF，根据AAS证得△BCE≌△CAF，推出BE=CF，CE=AF，即可得出结论；
（2）求出∠EBC=∠ACF，根据AAS证得△BEC≌△CFA，得出AF=CE，BE=CF，由EF=CE+CF，即可得出结论。