四川省万源中学2022年中考数学三轮：圆解答题+强化训练（有答案）

这是一份四川省万源中学2022年中考数学三轮：圆解答题+强化训练（有答案），共40页。试卷主要包含了如图，AB是⊙O的直径，点E等内容，欢迎下载使用。
四川省万源中学2022年中考数学三轮：圆解答题 强化训练
1、如图，点P是⊙O的直径AB延长线上的一点（PB＜OB），点E是线段OP的中点．
（1）尺规作图：在直径AB上方的圆上作一点C，使得EC＝EP，连接EC，PC（保留清晰作图痕迹，不要求写作法）；并证明PC是⊙O的切线；
（2）在（1）的条件下，若BP＝4，EB＝1，求PC的长．



2、如图，在Rt△ABC中，∠ACB＝90°，⊙O与BC，AC分别相切于点E，F，BO平分∠ABC，连接OA．
（1）求证：AB是⊙O的切线；
（2）若BE＝AC＝3，⊙O的半径是1，求图中阴影部分的面积．



3、如图，与⊙O相切于点，交⊙O于点，的延长线交于点，是⊙O上不与重合的点，．

（1）求的大小；
（2）若⊙O的半径为3，点在的延长线上，且，求证：与⊙O相切．


4、如图，AB是⊙O的直径，D为⊙O上一点，E为的中点，点C在BA的延长线上，且∠CDA＝∠B．
（1）求证：CD是⊙O的切线；
（2）若DE＝2，∠BDE＝30°，求CD的长．


5、如图，在Rt△ABC中，，以为直径的⊙O交于点，与过点的切线互相垂直，垂足为．

（1）求证：平分；
（2）若，求的值．


6、如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．


7、如图，在中，，以为直径的⊙O分别与，交于点，，过点作⊙O的切线，交于点．
（1）求证：；
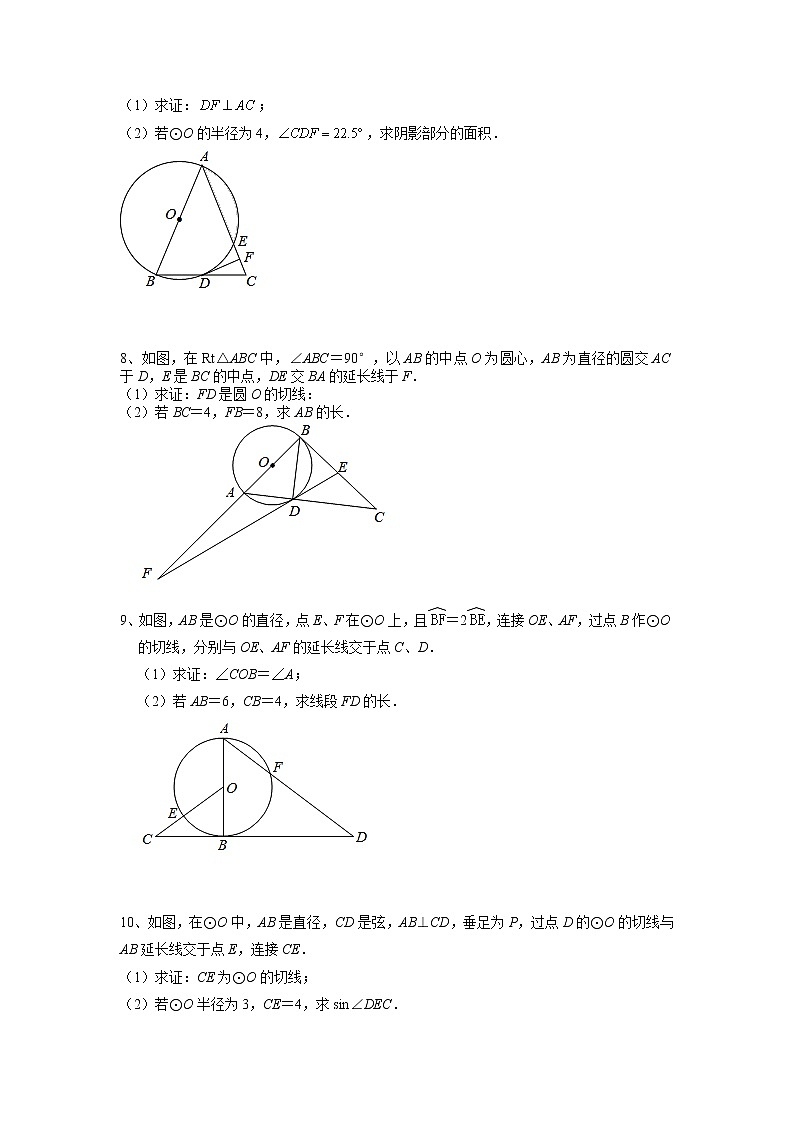
（2）若⊙O的半径为4，，求阴影部分的面积．



8、如图，在Rt△ABC中，∠ABC＝90°，以AB的中点O为圆心，AB为直径的圆交AC于D，E是BC的中点，DE交BA的延长线于F．
（1）求证：FD是圆O的切线：
（2）若BC＝4，FB＝8，求AB的长．


9、如图，AB是⊙O的直径，点E、F在⊙O上，且＝2，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．



10、如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为P，过点D的⊙O的切线与AB延长线交于点E，连接CE．
（1）求证：CE为⊙O的切线；
（2）若⊙O半径为3，CE＝4，求sin∠DEC．


11、如图，在⊙O中，∠AOB＝120°，＝，连接AC，BC，过点A作AD⊥BC，交BC的延长线于点D，DA与BO的延长线相交于点E，DO与AC相交于点F．
（1）求证：DE是⊙O的切线；
（2）若⊙O的半径为2，求线段DF的长．


12、如图，在Rt△AOB中，∠AOB＝90°，⊙O与AB相交于点C，与AO相交于点E，连接CE，已知∠AOC＝2∠ACE．
（1）求证：AB为⊙O的切线；
（2）若AO＝20，BO＝15，求CE的长．


13、如图，AB是⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD．
（1）求证：PD是⊙O的切线；
（2）当四边形POBD是平行四边形时，求∠APO的度数．


14、如图，已知AB是⊙O的直径，⊙O经过Rt△ACD的直角边DC上的点F，交AC边于点E，点F是弧EB的中点，∠C＝90°，连接AF．
（1）求证：直线CD是⊙O切线．
（2）若BD＝2，OB＝4，求tan∠AFC的值．



15、如图，四边形ABCD内接于⊙O，AC是直径，AB＝BC，连接BD，过点D的直线与CA的延长线相交于点E，且∠EDA＝∠ACD．
（1）求证：直线DE是⊙O的切线；
（2）若AD＝6，CD＝8，求BD的长．


16、如图，AB是⊙O直径，弦CD⊥AB，垂足为点E．弦BF交CD于点G，点P在CD延长线上，且PF＝PG．
（1）求证：PF为⊙O切线；
（2）若OB＝10，BF＝16，BE＝8，求PF的长．


17、如图，在Rt△ABC中，∠ACB＝90°，延长CA到点D，以AD为直径作⊙O，交BA的延长线于点E，延长BC到点F，使BF＝EF．
（1）求证：EF是⊙O的切线；
（2）若OC＝9，AC＝4，AE＝8，求BF的长．


18、如图，是⊙O的直径，点D在⊙O上，的延长线与过点B的切线交于点C，E为线段上的点，过点E的弦于点H．

（1）求证：；
（2）已知，，且，求的长．

19、AB是⊙O的直径，点C是⊙O上一点，连接AC、BC，直线MN过点C，满足．

（1）如图①，求证：直线MN是⊙O的切线；
（2）如图②，点D在线段BC上，过点D作于点H，直线DH交⊙O于点E、F，连接AF并延长交直线MN于点G，连接CE，且，若⊙O的半径为1，，求的值．

20、如图，△ABC内接于⊙O，点D在⊙O外，∠ADC＝90°，BD交⊙O于点E，交AC于点F，∠EAC＝∠DCE，∠CEB＝∠DCA，CD＝6，AD＝8．
（1）求证：AB∥CD；
（2）求证：CD是⊙O的切线；
（3）求tan∠ACB的值．


21、如图，四边形ABCD中，AD∥BC，AD⊥AB，AD＝AB＝1，DC＝，以A为圆心，AD为半径作圆，延长CD交⊙A于点F，延长DA交⊙A于点E，连结BF，交DE于点G．
（1）求证：BC为⊙A的切线；
（2）求cos∠EDF的值；
（3）求线段BG的长．


22、如图1，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若tan∠ADC＝，AC＝2，求⊙O的半径；
（3）如图2，在（2）的条件下，∠ADB的平分线DE交⊙O于点E，交AB于点F，连结BE．求sin∠DBE的值．



























参考答案
四川省万源中学2022年中考数学三轮：圆解答题 强化训练
1、如图，点P是⊙O的直径AB延长线上的一点（PB＜OB），点E是线段OP的中点．
（1）尺规作图：在直径AB上方的圆上作一点C，使得EC＝EP，连接EC，PC（保留清晰作图痕迹，不要求写作法）；并证明PC是⊙O的切线；
（2）在（1）的条件下，若BP＝4，EB＝1，求PC的长．

【解答】解：（1）如图，点C即为所求；

证明：∵点E是线段OP的中点，
∴OE＝EP，
∵EC＝EP，
∴OE＝EC＝EP，
∴∠COE＝∠ECO，∠ECP＝∠P，
∵∠COE+∠ECO+∠ECP+∠P＝180°，
∴∠ECO+∠ECP＝90°，
∴OC⊥PC，且OC是⊙O的半径，
∴PC是⊙O的切线；
（2）∵BP＝4，EB＝1，
∴OE＝EP＝BP+EB＝5，
∴OP＝2OE＝10，
∴OC＝OB＝OE+EB＝6，
在Rt△OCP中，根据勾股定理，得PC＝＝8．
则PC的长为8．

2、如图，在Rt△ABC中，∠ACB＝90°，⊙O与BC，AC分别相切于点E，F，BO平分∠ABC，连接OA．
（1）求证：AB是⊙O的切线；
（2）若BE＝AC＝3，⊙O的半径是1，求图中阴影部分的面积．

【解答】（1）证明：
连接OE，OF，过点O作OD⊥AB于点D，

∵BC与⊙O相切于点E，
∴OE⊥BC，
∵BO是∠ABC的平分线，
∴OD═OE，OE是圆的一条半径，
∴AB是⊙O的切线，
故：AB是⊙O的切线．
（2）∵BC、AC与圆分别相切于点E、点F，
∴OE⊥BC，OF⊥AC，
∴四边形OECF是正方形，
∴OE═OF═EC═FC═1，
∴BC═BE+EC═4，又AC═3，
∴S阴影═（S△ABC﹣S正方形OECF﹣优弧所对的S扇形EDF）
═×（×4×3﹣1×1﹣）
═﹣．
故图中阴影部分的面积是：﹣．

3、如图，与⊙O相切于点，交⊙O于点，的延长线交于点，是⊙O上不与重合的点，．

（1）求的大小；
（2）若⊙O的半径为3，点在的延长线上，且，求证：与⊙O相切．
【详解】解：(1)连接，

∵与⊙O相切于点，
∴，
∵，∴，
∴，则．
由同弧所对的圆周角等于圆心角的一半可知：
．
故答案为：．
(2)连接，

由(1)得，，
∵，，∴，
∴，∴．
在与中，
∴，
∴．
又点在⊙O上，故与⊙O相切．

4、如图，AB是⊙O的直径，D为⊙O上一点，E为的中点，点C在BA的延长线上，且∠CDA＝∠B．
（1）求证：CD是⊙O的切线；
（2）若DE＝2，∠BDE＝30°，求CD的长．

【解答】（1）证明：连结OD，如图所示：

∵AB是直径，
∴∠BDA＝90°，
∴∠BDO+∠ADO＝90°，
又∵OB＝OD，∠CDA＝∠B，
∴∠B＝∠BDO＝∠CDA，
∴∠CDA+∠ADO＝90°，
∴OD⊥CD，且OD为⊙O半径，
∴CD是⊙O的切线；
（2）解：连结OE，如图所示：

∵∠BDE＝30°，
∴∠BOE＝2∠BDE＝60°，
又∵E为的中点，
∴∠EOD＝60°，
∴△EOD为等边三角形，
∴ED＝EO＝OD＝2，
又∵∠BOD＝∠BOE+∠EOD＝120°，
∴∠DOC＝180°﹣∠BOD＝180°﹣120°＝60°，
在Rt△DOC中，∠DOC＝60°，OD＝2，
∴tan∠DOC＝tan60°＝＝＝，
∴CD＝2．

5、如图，在Rt△ABC中，，以为直径的⊙O交于点，与过点的切线互相垂直，垂足为．

（1）求证：平分；
（2）若，求的值．
【详解】（1）如图，连接OD
由圆的切线的性质得：



又


则平分；
（2）如图，连接BD
由圆周角定理得：





在△ADE和△BCD中，
∴△ADE≌△BCD

设，则，且
在和中，
∴△ACB∽△BCD
，即
解得或（不符题意，舍去）
经检验，是所列分式方程的解

则在Rt△ABC中，
故的值为．


6、如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．

【解答】（1）证明：连接DO，如图，

∵∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD，
∴DE与⊙O相切；

（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE＝BC，
∴BC＝5，
∴BD＝＝＝4，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴＝，
∴＝，
∴AC＝，
∴⊙O直径的长为．
7、如图，在中，，以为直径的⊙O分别与，交于点，，过点作⊙O的切线，交于点．
（1）求证：；
（2）若⊙O的半径为4，，求阴影部分的面积．

【解答】（1）证明：连接，
，
，
，
，
，
，
是⊙O的切线，
，
．
（2）解：连接，
，，
，
，
，
，
⊙O的半径为4，
，，
．


8、如图，在Rt△ABC中，∠ABC＝90°，以AB的中点O为圆心，AB为直径的圆交AC于D，E是BC的中点，DE交BA的延长线于F．
（1）求证：FD是圆O的切线：
（2）若BC＝4，FB＝8，求AB的长．

【解答】（1）证明：
连接OD，
由题可知∠ABC＝90°，
∵AB为直径，
∴∠ADB＝∠BDC＝90°，
∵点E是BC的中点，
∴DE＝BC＝BE＝EC，
∴∠EDC＝∠ECD，
又∵∠ECD+∠CBD＝90°，∠ABD+∠CBD＝90°，
∴∠ECD＝∠ABD，
∵OB和OD是圆的半径，
∴∠ODB＝∠OBD，
∴∠ODB+∠BDE＝∠EDC+∠BDE＝90°，
即∠ODE＝90°，
故：FE是⊙O的切线．
（2）由（1）可知BE＝EC＝DE＝BC＝2，
在Rt△FBE中，FE＝＝＝，
∴FD＝FE﹣DE＝﹣2，
又∵在Rt△FDO和Rt△FBE中有：∠FDO＝∠FBE＝90°，∠OFD＝∠EFB，
∴△FDO∽△FBE，
∴，即，
求得OD＝，
∴AB＝2OD＝﹣1，
故：AB长为﹣1．
9、如图，AB是⊙O的直径，点E、F在⊙O上，且＝2，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．

【解答】（1）证明：取的中点M，连接OM、OF，
∵＝2，
∴＝＝，
∴∠COB＝∠BOF，
∵∠A＝∠BOF，
∴∠COB＝∠A；
（2）解：连接BF，如图，
∵CD为⊙O的切线，
∴AB⊥CD，
∴∠OBC＝∠ABD＝90°，
∵∠COB＝∠A，
∴△OBC∽△ABD，
∴＝，即＝，解得BD＝8，
在Rt△ABD中，AD＝＝＝10，
∵AB是⊙O的直径，
∴∠AFB＝90°，
∵∠BDF＝∠ADB，
∴Rt△DBF∽Rt△DAB，
∴＝，即＝，解得DF＝．


10、如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为P，过点D的⊙O的切线与AB延长线交于点E，连接CE．
（1）求证：CE为⊙O的切线；
（2）若⊙O半径为3，CE＝4，求sin∠DEC．

【解答】证明：（1）连接OC，OD，
∵OC＝OD，AB⊥CD，
∴∠COE＝∠DOE，
在△COE和△DOE中，
，
∴△COE≌△DOE（SAS），
∴∠OCE＝∠ODE，
∵DE是⊙O的切线，
∴∠ODE＝90°，
∴∠OCE＝90°，
∵OC是⊙O的半径，
∴CE为⊙O的切线；
（2）解：过D作DF⊥CE于F，
由（1）知，∠OCE＝90°，
在Rt△OCE中，∵CE＝4，OC＝3，
∴OE＝＝＝5，
∵AB⊥CD，
∴S△OCE＝OC•CE＝CP•OE，
∴3×4＝5CP，
∴CP＝，
∵OC＝OD，AB⊥CD，
∴CP＝DP，
∴CD＝2CP＝，
在Rt△CPE中，PE＝＝＝，
∵CE，DE是⊙O的切线，
∴DE＝CE＝4，
∵S△CDE＝CE•DF＝CD•PE，
∴4DF＝×，
∴DF＝，
在Rt△DEF中，sin∠DEC＝＝＝．

11、如图，在⊙O中，∠AOB＝120°，＝，连接AC，BC，过点A作AD⊥BC，交BC的延长线于点D，DA与BO的延长线相交于点E，DO与AC相交于点F．
（1）求证：DE是⊙O的切线；
（2）若⊙O的半径为2，求线段DF的长．

【解答】解：（1）如图，连接OC，
∵＝，
∴AC＝BC，
又∵OA＝OB，OC＝OC，
∴△OAC≌△OBC（SSS），
∴∠AOC＝∠BOC＝∠AOB＝60°，
∴△AOC、△BOC是等边三角形，
∴OA＝AC＝CB＝OB，
∴四边形OACB是菱形，
∴OA∥BD，
又∵AD⊥BD，
∴OA⊥DE，
∴DE是⊙O的切线；
（2）由（1）得AC＝OA＝2，∠OAC＝60°，∠DAC＝90°﹣60°＝30°，
在Rt△ACD中，∠DAC＝30°，AC＝2，
∴DC＝AC＝1，AD＝AC＝，
在Rt△AOD中，由勾股定理得，
OD＝＝＝，
∵OA∥BD，
∴△CFD∽△AFO，
∴＝，
又∵＝sin30°＝，AC＝OA＝2，
∴＝，
∴＝，
即DF＝OD＝．

12、如图，在Rt△AOB中，∠AOB＝90°，⊙O与AB相交于点C，与AO相交于点E，连接CE，已知∠AOC＝2∠ACE．
（1）求证：AB为⊙O的切线；
（2）若AO＝20，BO＝15，求CE的长．

【解答】（1）证明：∵OC＝OE，
∴∠OCE＝∠OEC，
∵∠AOC＝2∠ACE，
∴∠OCA＝∠OCE+∠ACE＝（∠OCE+∠OEC+∠AOC）＝＝90°，
∴OC⊥AB，
∴AB为⊙O的切线；
（2）解：作EH⊥AC于H，
∵AO＝20，BO＝15，
∴AB＝＝＝25，
∵，
即，
∴OC＝12，
∴AE＝OA﹣OE＝20﹣12＝8，
∵EH⊥AC，OC⊥AC，
∴EH∥OC，
∴△AEH∽△AOC，
∴＝，
即＝，
∴EH＝，
∵BC＝＝＝9，
∴AC＝AB﹣BC＝25﹣9＝16，
∵AH＝＝＝，
∴CH＝AC﹣AH＝16﹣＝，
∴CE＝＝＝．

13、如图，AB是⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD．
（1）求证：PD是⊙O的切线；
（2）当四边形POBD是平行四边形时，求∠APO的度数．

【解答】（1）证明：连接OD，

∵PA切⊙O于A，
∴PA⊥AB，
即∠PAO＝90°，
∵OP∥BD，
∴∠DBO＝∠AOP，∠BDO＝∠DOP，
∵OD＝OB，
∴∠BDO＝∠DBO，
∴∠DOP＝∠AOP，
在△AOP和△DOP中
，
∴△AOP≌△DOP（SAS），
∴∠PDO＝∠PAO，
∵∠PAO＝90°，
∴∠PDO＝90°，
即OD⊥PD，
∵OD过O，
∴PD是⊙O的切线；

（2）解：
由（1）知：△AOP≌△DOP，
∴PA＝PD，
∵四边形POBD是平行四边形，
∴PD＝OB，
∵OB＝OA，
∴PA＝OA，
∵∠PAO＝90°，
∴∠APO＝∠AOP＝45°．
14、如图，已知AB是⊙O的直径，⊙O经过Rt△ACD的直角边DC上的点F，交AC边于点E，点F是弧EB的中点，∠C＝90°，连接AF．
（1）求证：直线CD是⊙O切线．
（2）若BD＝2，OB＝4，求tan∠AFC的值．

【解答】（1）证明：连结OF，BE，如图：
∵AB是⊙O的直径，
∴∠AEB＝90°，
∵∠C＝90°，
∴∠AEB＝∠ACD，
∴BE∥CD，
∵点F是弧BE的中点，
∴OF⊥BE，
∴OF⊥CD，
∵OF为半径，
∴直线DF是⊙O的切线；
（2）解：∵∠C＝∠OFD＝90°，
∴AC∥OF，
∴△OFD∽△ACD，
∴＝，
∵BD＝2，OF＝OB＝4，
∴OD＝6，AD＝10，
∴AC＝＝＝，
∴CD＝＝＝，
∵AC∥OF，OA＝4，
∴＝，即＝，
解得：CF＝，
∴tan∠AFC＝＝＝．


15、如图，四边形ABCD内接于⊙O，AC是直径，AB＝BC，连接BD，过点D的直线与CA的延长线相交于点E，且∠EDA＝∠ACD．
（1）求证：直线DE是⊙O的切线；
（2）若AD＝6，CD＝8，求BD的长．

【解答】（1）证明：连接OD，
∵OC＝OD，
∴∠OCD＝∠ODC，
∵AC是直径，
∴∠ADC＝90°，
∵∠EDA＝∠ACD，
∴∠ADO+∠ODC＝∠EDA+∠ADO，
∴∠EDO＝∠EDA+∠ADO＝90°，
∴OD⊥DE，
∵OD是半径，
∴直线DE是⊙O的切线．

（2）解法一：过点A作AF⊥BD于点F，则∠AFB＝∠AFD＝90°，
∵AC是直径，
∴∠ABC＝∠ADC＝90°，
∵在Rt△ACD中，AD＝6，CD＝8，
∴AC2＝AD2+CD2＝62+82＝100，
∴AC＝10，
∵在Rt△ABC中，AB＝BC，
∴∠BAC＝∠ACB＝45°，
∵，
∴，
∵∠ADB＝∠ACB＝45°，
∵在Rt△ADF中，AD＝6，
∵，
∴，
∴，
∵在Rt△ABF中，
∴，
∴，
∴．

解法二：过点B作BH⊥BD交DC延长线于点H．
∴∠DBH＝90°，
∵AC是直径，
∴∠ABC＝90°，
∵∠ABD＝90°﹣∠DBC∠CBH＝90°﹣∠DBC，
∴∠ABD＝∠CBH，
∵四边形ABCD内接于⊙O，
∴∠BAD+∠BCD＝180°，
∵∠BCD+∠BCH＝180°，
∴∠BAD＝∠BCH，
∵AB＝CB，
∴△ABD≌△CBH（ASA），
∴AD＝CH，BD＝BH，
∵AD＝6，CD＝8，
∴DH＝CD+CH＝14，
在Rt△BDH中，∵BD2＝DH2﹣BH2＝98，
∴．


16、如图，AB是⊙O直径，弦CD⊥AB，垂足为点E．弦BF交CD于点G，点P在CD延长线上，且PF＝PG．
（1）求证：PF为⊙O切线；
（2）若OB＝10，BF＝16，BE＝8，求PF的长．

【解答】
（1）证明：连接OF，
∵PF＝PG，
∴∠PFG＝∠PGF，
∵∠BGE＝∠PGF，
∴∠PFG＝∠BGE，
∵OF＝OB，
∴∠OFB＝∠OBF，
∵CD⊥AB，
∴∠BGE+∠OBF＝90°，
∴∠PFG+∠OFB＝90°，
∵OF是⊙O半径，
∴PF为⊙O切线；

（2）解：连接AF，过点P作PM⊥FG，垂足为M，
∵AB是⊙O直径，
∴∠AFB＝90°，
∴AB2＝AF2+BF2，
∵OB＝10，
∴AB＝20，
∵BF＝16，
∴AF＝12，
在Rt△ABF中，tanB＝，cosB＝，
在Rt△BEG中，，，
∴GE＝6，GB＝10，
∵BF＝16，
∴FG＝6，
∵PM⊥FG，PF＝PG，
∴MG＝FG＝3，
∵∠BGE＝∠PFM，∠PMF＝∠BEG＝90°，
∴△PFM∽△BGE，
∴，即，
解得：PF＝5，
∴PF的长为5．

17、如图，在Rt△ABC中，∠ACB＝90°，延长CA到点D，以AD为直径作⊙O，交BA的延长线于点E，延长BC到点F，使BF＝EF．
（1）求证：EF是⊙O的切线；
（2）若OC＝9，AC＝4，AE＝8，求BF的长．

【解答】证明：（1）连接OE，
∵OA＝OE，
∴∠OEA＝∠OAE，
在Rt△ABC中，∠ACB＝90°，
∴∠BAC+∠B＝90°，
∵BF＝EF，
∴∠B＝∠BEF，
∵∠OAE＝∠BAC，
∴∠OEA＝∠BAC，
∴∠OEF＝∠OEA+∠BEF＝∠BAC+∠B＝90°，
∴OE⊥EF，
∵OE是⊙O的半径，
∴EF是⊙O的切线；

（2）解：连接DE，
∵OC＝9，AC＝4，
∴OA＝OC﹣AC＝5，
∵AD＝2OA，
∴AD＝10，
∵AD是⊙O的直径，
∴∠AED＝90°，
在Rt△ADE中，
∵DE＝＝＝6，
∴cos∠DAE＝＝＝，
在Rt△ABC中，cos∠BAC＝＝，
∵∠BAC＝∠DAE，
∴＝，
∴AB＝5，
∴BE＝AB+AE＝5+8＝13，
∵OD＝OE，
∴∠ODE＝∠OED，
∵EF是⊙O的切线，
∴∠FEO＝90°，
∵∠OED+∠OEA＝90°，∠FEB+∠OEA＝90°，
∴∠FEB＝∠OED，
∴∠B＝∠FEB＝∠OED＝∠ODE，
∴△FBE∽△ODE，
∴＝，
∴＝，
∴BF＝．

18、如图，是⊙O的直径，点D在⊙O上，的延长线与过点B的切线交于点C，E为线段上的点，过点E的弦于点H．

（1）求证：；
（2）已知，，且，求的长．
【详解】解：（1）∵OA=OD，
∴∠ODA=∠OAD，
∵BC和AB相切，
∴∠ABC=90°，
∵DG为圆O直径，
∴∠DAG=90°，
∵∠C=180°-∠CAB-∠ABC，∠AGD=180°-∠DAG-∠ADO，
∴∠C=∠AGD；
（2）连接BD，
∵AB为直径，
∴∠ADB=∠CDB=90°，
∵，，
∴BD=，
∵OA=OB=OD=OG，∠AOG=∠BOD，
∴△BOD≌AOG（SAS），
∴AG=BD=，
∵FG⊥AB，BC⊥AB，
∴FG∥BC，
∴∠AEG=∠C，
∵∠EAG=∠CDB=90°，AG=BD，
∴△AEG≌△DCB（AAS），
∴EG=BC=6，AE=CD=4，
∵AH⊥FG，AB为直径，
∴AH=AE×AG÷EG=，FH=GH，
∴FH=GH==，
∴FG=2HG=，
∴EF=FG-EG=-6=．

19、AB是⊙O的直径，点C是⊙O上一点，连接AC、BC，直线MN过点C，满足．

（1）如图①，求证：直线MN是⊙O的切线；
（2）如图②，点D在线段BC上，过点D作于点H，直线DH交⊙O于点E、F，连接AF并延长交直线MN于点G，连接CE，且，若⊙O的半径为1，，求的值．
【详解】解：（1）证明：连接OC，如图，
∵AB是⊙O的直径，
∴，
∴，
∵，
∴，
∵，
∴，即，
∴MN是⊙O的切线；

（2）如图②，∵，即，∴，
∵∠2=∠3，∠1=∠2，
∴∠1=∠3，
∵，
∴∠1+∠AGC=90°，
∵∠3+∠ECD=90°，
∴，
又∵，
∴∽△ACG，
∴，
∴．

20、如图，△ABC内接于⊙O，点D在⊙O外，∠ADC＝90°，BD交⊙O于点E，交AC于点F，∠EAC＝∠DCE，∠CEB＝∠DCA，CD＝6，AD＝8．
（1）求证：AB∥CD；
（2）求证：CD是⊙O的切线；
（3）求tan∠ACB的值．

【解答】（1）证明：∵∠BAC＝∠CEB，∠CEB＝∠DCA，
∴∠BAC＝∠DCA，
∴AB∥CD；
（2）证明：连接EO并延长交⊙O于G，连接CG，如图1所示：
则EG为⊙O的直径，
∴∠ECG＝90°，
∵OC＝OG，
∴∠OCG＝∠EGC，
∵∠EAC＝∠EGC，∠EAC＝∠DCE，
∴∠DCE＝∠EGC＝∠OCG，
∵∠OCG+∠OCE＝∠ECG＝90°，
∴∠DCE+∠OCE＝90°，即∠DCO＝90°，
∵OC是⊙O的半径，
∴CD是⊙O的切线；
（3）解：在Rt△ADC中，由勾股定理得：AC＝＝＝10，
∴cos∠ACD＝＝＝，
∵CD是⊙O的切线，AB∥CD，
∴∠ABC＝∠ACD＝∠CAB，
∴BC＝AC＝10，AB＝2BC•cos∠ABC＝2×10×＝12，
过点B作BG⊥AC于C，如图2所示：
设GC＝x，则AG＝10﹣x，
由勾股定理得：AB2﹣AG2＝BG2＝BC2﹣GC2，
即：122﹣（10﹣x）2＝102﹣x2，
解得：x＝，
∴GC＝，
∴BG＝＝＝，
∴tan∠ACB＝＝＝．


21、如图，四边形ABCD中，AD∥BC，AD⊥AB，AD＝AB＝1，DC＝，以A为圆心，AD为半径作圆，延长CD交⊙A于点F，延长DA交⊙A于点E，连结BF，交DE于点G．
（1）求证：BC为⊙A的切线；
（2）求cos∠EDF的值；
（3）求线段BG的长．

【解答】（1）证明：∵AD⊥AB，
∴∠BAD＝90°，
∵AD∥BC，
∴∠ABC＝180°﹣∠BAD＝90°，
∵AB＝AD，
∴BC为⊙A的切线；

（2）解：如图1，过点D作DH⊥BC于H，
∴∠DHB＝90°，
由（1）知，∠BAD＝∠ABD＝90°，
∴∠ABD＝∠BAD＝∠BHD＝90°，
∴四边形ABHD为矩形，
∵AB＝AD＝1，
∴矩形ABHD是正方形，
∴BH＝DH＝AB＝1，
在Rt△DHC中，CD＝，根据勾股定理得，CH＝＝2，
∴cosC＝＝＝，
∵AD∥BC，
∴∠EDF＝∠C，
∴cos∠EDF＝cosC＝；

（3）如图2，
过点A作AM⊥DF于M，则DF＝2DM，∠AMD＝90°，
在Rt△AMD中，AD＝1，cos∠EDF＝，
∴DM＝AD•cos∠EDF＝1×＝，
∴DF＝2DM＝，
∴CF＝DF+CD＝+＝，
∵AD∥BC，
∴△DFG∽△CFB，
∴，
由（1）知，BC＝1+2＝3，
∴＝，
∴DG＝，
∴AG＝DG﹣AD＝，
在Rt△BAG中，BG＝＝＝．


22、如图1，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若tan∠ADC＝，AC＝2，求⊙O的半径；
（3）如图2，在（2）的条件下，∠ADB的平分线DE交⊙O于点E，交AB于点F，连结BE．求sin∠DBE的值．

【解答】解：（1）CD与⊙O相切，理由：
如图1，连接OD，
∵OB＝OD，
∴∠ODB＝∠CBD，
∵∠CDA＝∠CBD，
∴∠CDA＝∠ODB，
∵AB为⊙O的直径，
∴∠ADB＝∠ADO+∠ODB＝90°，
∴∠CDA+∠ADO＝90°，
∴∠CDO＝90°，
∴OD⊥CD，
∴CD与⊙O相切；

（2）由（1）知，∠CBD＝∠ADC，
∵tan∠ADC＝，
∴tan∠CBD＝，
在Rt△ADB中，tan∠CBD＝＝，
∵∠C＝∠C，∠ADC＝∠CBD，
∴△CAD∽△CDB，
∴，
∴CD＝2CA＝4，
∴CB＝2CD＝8，
∴AB＝CB﹣CA＝8﹣2＝6，
∴OA＝OB＝AB＝3；

（3）如图2，连接OE，过点E作EG⊥BD于G，
∵DE平分∠ADB，
∴∠ADE＝∠BDE＝45°，
∴∠BOE＝2∠BDE＝90°，
∴BE＝＝3，
在Rt△ABD中，AD2+BD2＝AB2＝62，
∵，
∴AD＝，BD＝，
∵EG⊥BD，∠BDE＝45°，
∴∠DEG＝∠BDE＝45°，
∴DG＝EG，
设DG＝EG＝x，则BG＝BD﹣DG＝﹣x，
在Rt△BEG中，EG2+BG2＝BE2＝（3）2＝18，
∴x2+（﹣x）2＝18，
∴x＝或x＝（舍），
∴EG＝，
∴sin∠DBE＝＝．