初中数学华师大版八年级下册18.1 平行四边形的性质集体备课课件ppt

这是一份初中数学华师大版八年级下册18.1 平行四边形的性质集体备课课件ppt，共26页。PPT课件主要包含了ABCD，复习回顾，随堂检测，运用拓展，中考链接等内容，欢迎下载使用。
1.定义: 有两组对边分别平行的四边形 叫做平行四边形。
读作：平行四边形ABCD
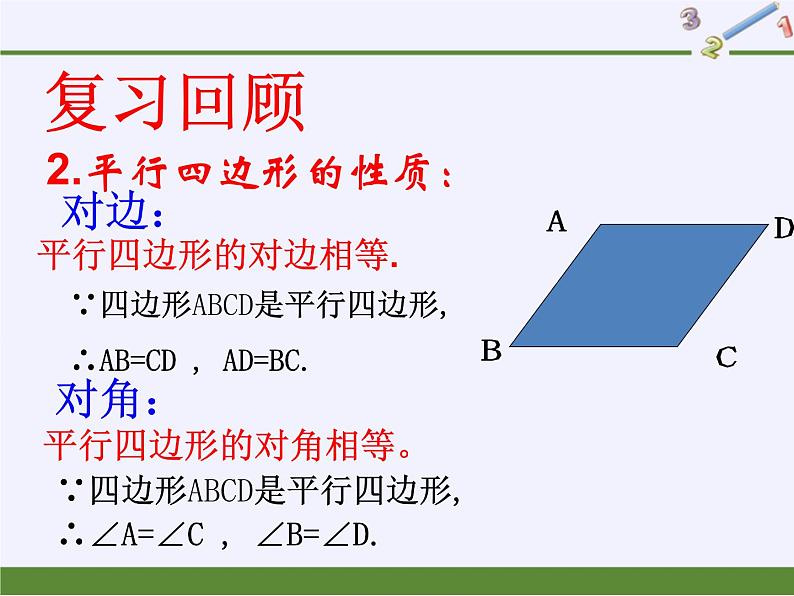
2.平行四边形的性质：
平行四边形的对边相等.
平行四边形的对角相等。
∵四边形ABCD是平行四边形,∴∠A=∠C , ∠B=∠D.
∵四边形ABCD是平行四边形,∴AB=CD , AD=BC.
18.1 平行四边形的性质(2)
18.1.2 平行四边形与邻边有关的计算和证明
3、培养学生推理能力和逻辑思维能力。
1、能够灵活运用平行四边形的性质1,2;
2、结合平行四边形性质1,2解决与邻边相关的计算和证明问题.（重点）
如图，在方格纸上画两条互相平行的直线，在其中一条直线上任取若干点，过这些点作另一条直线的垂线，用刻度尺量出平行线之间的垂线段的长度。
你能发现什么结论？试说明其中的道理。
发现：这些垂线段的长度都相等。
两条直线平行，其中一条直线上任一点到另一条直线的距离，叫做两条平行线直接的距离。平行线之间的距离处处相等。
新知探究（一）：阅读教材75页例3内容，思考：1.思考例3平行四边行的周长为24该如何表示？2.如何找等量关系？为什么？3.运用了什么思想？4.整理你的解题过程与小组成员对比，看谁的思路更清晰！
例3：已知平行四边形的周长是24，相邻两边的长度相差4，求该平行四边形相邻两边的长.
解：设AB的长为 x ,则BC的长为 x+4.根据已知，可得 2（AB+BC）=24,即 2（x+x+4）=24, 4x+8=24,解得 x=4.所以，该平行四边形相邻两边的长分别为4和8.
1. 已知平行四边形ABCD的周长为32，AB=4，则BC的长为________.
解析：∵四边形ABCD是平行四边形，∴AB=CD，AD=BC，∵平行四边形ABCD的周长是32，∴2（AB+BC）=32，∴2（4+BC）=32，∴BC=12．
2. 如图，平行四边形ABCD周长是28cm，△ABC的周长是22cm，则AC长（　　）A.14cm B.12cm C.10cm D.8cm
解析：∵ ABCD的周长是28cm，∴AB+BC=14cm，∵△ABC的周长是22cm，∴AC=22-（AB+BC）=8cm， 故选D．
1. 在平行四边形中，两邻边长之和等于周长的一半.
2.在求平行四边形各边长时，可设一元一次方程或二元一次方程组求解.
新知探究（二）：阅读教材76页例4内容，思考：1.例4问题的解决运用了平行四边形什么知识？2.整理解题思路。
例4 已知：如图，在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，求证：CE+CD=AD．
证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB=CD，AD=BC，∴∠AEB=∠DAE，∵AE平分∠BAD, ∴∠BAE=∠DAE，∴∠BAE=∠AEB，∴AB=BE=CD，∴CE+CD=CE+BE=BC=AD.
1. 如图，平行四边形ABCD的周长为20，AE平分∠BAD，若CE=2，则AB长为（　　）A.8 B.10 C.6 D.4
2. 如图，在平行四边形ABCD中，AE平分∠BAD，已知∠AEB=63°，则∠D的度数为（　　）A.63° B.72° C.54° D.60°
平行四边形一内角的平分线与对边相交于一点，可得到一个等腰三角形.
1、已知平行四边形的周长为32cm，两邻边的长相等，求该平行四边形各边的长.2、如果平行四边形的一组邻边的长相等，且等于其较短的对角线的长，而此对角线的长为4cm,求此平行四边形各内角的大小及各边的长.
3.如图，在□ABCD中，AE平分∠BAD,BE平分∠ABC，且AE,BE相交于CD上的一点E，求证：AE┴BE.
解：∵在□ABCD中, 对边相等, 又∵□ABCD的周长为60cm. ∴AB + BC=30cm. 又AB∶BC=3∶2，即AB=1.5BC. 则 1.5BC + BC=30 , 解得 BC=12 (cm). 而 AB=1.5×12=18 (cm).
1、 已知平行四边形ABCD的周长为60cm，两邻边AB，BC长的比为3∶2，求AB和BC的长度 .
2.如图，四边形ABCD是平行四边形，求： （1）∠ADC，∠BCD的度数； （2）边AB，BC的长度.
解：（1）∵四边形ABCD是平行四边形
∴∠B=∠ADC AB∥CD
∴∠B+∠BCD=180°
∴∠ADC=∠B=56°
∠BCD=180°－∠B=180°－56°=124°
（2）∵四边形ABCD是平行四边形
∴AD=BC,AB=CD(平行四边形对边相等)
∵AD=30,CD=25 ∴BC=30,AB=25.
3.已知如图： ABCD中，AD=8，AB=6，DE平分∠ADC交BC于E，则BE= ．
解析：∵DE平分∠ADC，∴ ∠ADE=∠CDE，∵ ABCD中AD∥BC，∴∠ADE=∠CED，∴ ∠CDE=∠CED ∴CE=CD，
∵在 ABCD中，AB=6，AD=8，∴CD=AB=6，BC=AD=8，（平行四边形的对边相等）∴BE=BC-CE=8-6=2．
如图，在□ABCD中，BE平分∠ABC交DC于E，AF 平分∠DAB交DC于F，若AB =5，BC=3，求EF的长。
平行四边形两邻边的特点
2.平行四边形一内角的平分线与对边相交于一点，可得到一个等腰三角形.
学习了本节课你有哪些收获？