



华师大版八年级下册17.5实践与探索授课ppt课件
展开17.5(3)实践与探索
学习目标:1、通过描点,拟合变量之间的函数关系,导出函数的关系式。2、理解建模思想在解决实际问题中的应用,寻找实际问题中的近似函数关系。
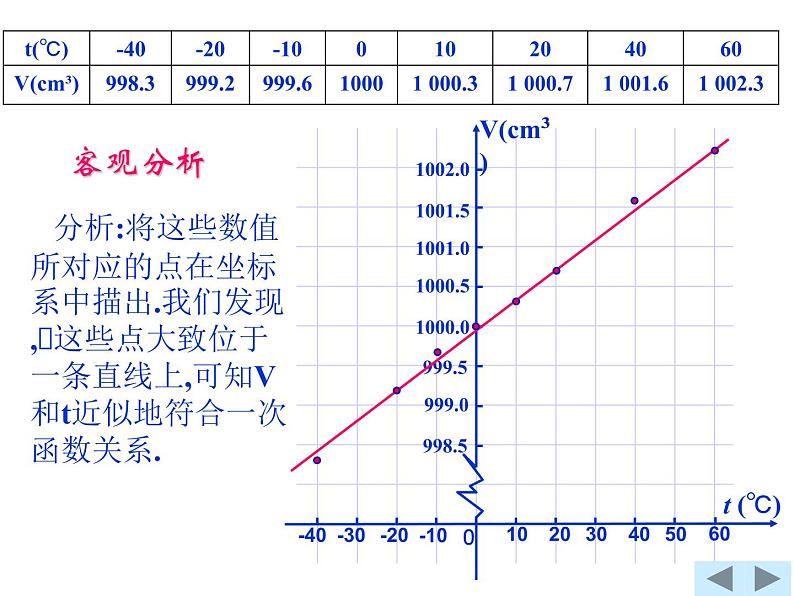
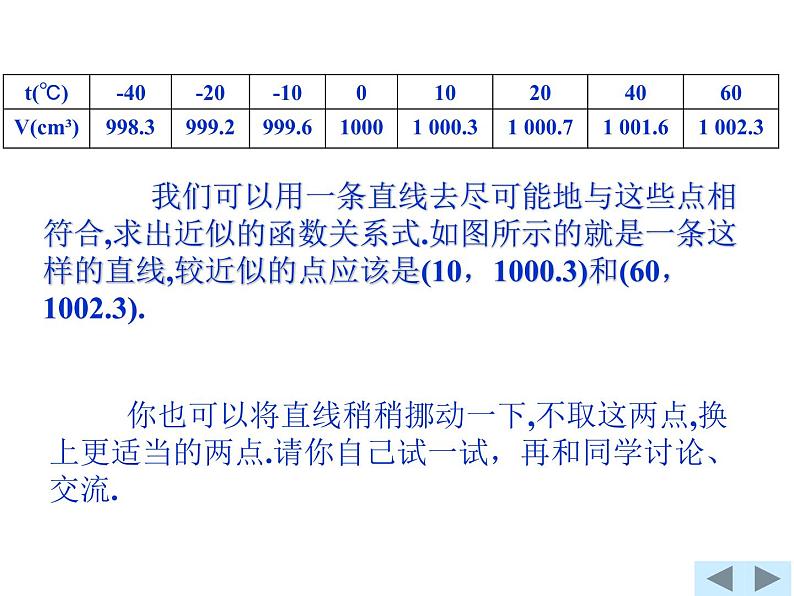
为了研究某合金材料的体积V(cm³)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系?
分析:将这些数值所对应的点在坐标系中描出.我们发现,这些点大致位于一条直线上,可知V和t近似地符合一次函数关系.
我们可以用一条直线去尽可能地与这些点相符合,求出近似的函数关系式.如图所示的就是一条这样的直线,较近似的点应该是(10,1000.3)和(60,1002.3).
你也可以将直线稍稍挪动一下,不取这两点,换上更适当的两点.请你自己试一试,再和同学讨论、交流.
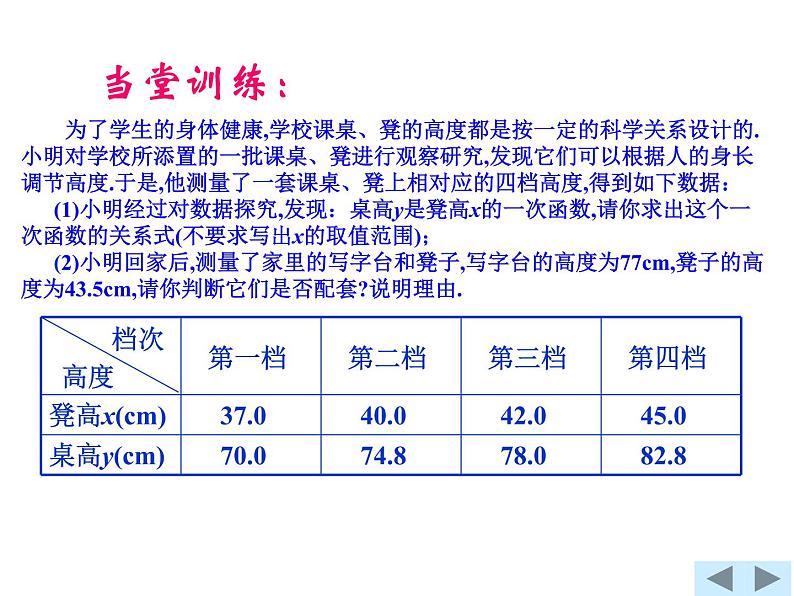
为了学生的身体健康,学校课桌、凳的高度都是按一定的科学关系设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据: (1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围); (2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
一次函数关系式是y=1.6x+10.8.
(2)当x=43.5时y=1.6×43.5+10.8=80.4≠77.
答: 一次函数关系式是y=1.6x+10.8;
(1)设一次函数为y=kx+b (k≠0),
将表中数据任取两组,不妨取(37.0,70.0)和(42.0,78.0)代入,得
小明家里的写字台和凳子不配套 .
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗?(2)问43码的鞋相当于多少厘米的鞋?
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
所以y与x的函数关系式可能是:
(2)当y=43时,2x-10=43,
(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
x=23时, y=36; x=26时, y=42.
我们曾采用待定系数法求得一次函数和反比例函数的关系式。但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究。
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式。
1.在实践活动中采集一组有限个有序数对。2.将这些有序数对作为点的坐标在坐标平面内描出相应的点。3.对比已经学过的函数图象,确定这些点组成的图形类似于某 一类函数图象,并写出这一函数的一般式。4.通过已知点的坐标确定函数一般式中待定系数的值。5.根据实际问题确定自变量的取值范围。6.根据函数图象确定你所研究的问题中变量的变化规律。
小明在做电学实验时,电路图如图所示.在保持电压不变的情况下,改换不同的电阻R,并用电流表测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中的各点,并画出该函数的近似图象;(2)观察图象,猜想I与R之间的函数关系,并求出函数解析式;(3)小明将一个未知电阻值的电阻串联到电路中,查得电流表的度数为0.5安培,你知道这个电阻的电阻值吗?
初中数学26.3 实践与探索精品ppt课件: 这是一份初中数学26.3 实践与探索精品ppt课件,共23页。PPT课件主要包含了复习引入,x≤2,0-6,x-6或x1,x1-4x22,x-4或x2,x-1,合作探究,x2h,方法二等内容,欢迎下载使用。
数学华师大版6.3 实践与探索课前预习课件ppt: 这是一份数学华师大版6.3 实践与探索课前预习课件ppt,共4页。
初中6.3 实践与探索评课ppt课件: 这是一份初中6.3 实践与探索评课ppt课件,共17页。PPT课件主要包含了3实践与探索,问题2,经检验符合题意等内容,欢迎下载使用。













