2021-2022学年河北省石家庄市新乐市七年级（下）期中数学试卷（含解析）

展开

这是一份2021-2022学年河北省石家庄市新乐市七年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年河北省石家庄市新乐市七年级（下）期中数学试卷副标题题号一二三总分得分      一、选择题（本大题共16小题，共42.0分）有下列方程：；；；；其中，二元一次方程有A. 个 B. 个 C. 个 D. 个计算：A. B. C. D. 的计算结果是A. B. C. D. 解方程组时，若将可得A. B. C. D. 如图，直线，则为A.
B.
C.
D. 计算：A. B. C. D. 如图，直线，相交于点，平分，若，则的度数是A.
B.
C.
D. 下列计算：；；；其中，错误的个数是A. B. C. D. 年月国家统计局公布了第七次人口普查结果，我国人口数约为其中数据用科学记数法表示为A. B. C. D. 两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆，同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线，食指代表截线下列三幅图依次表示
A. 同位角、同旁内角、内错角 B. 同位角、内错角、同旁内角
C. 同位角、对顶角、同旁内角 D. 同位角、内错角、对顶角如图，在下列条件中，不能判定直线与平行的是A.
B.
C.
D.
已知，，，则、、的大小关系是            A. B. C. D. 若关于，的方程组的解是，则方程组的解是A. B. C. D. 九章算术是中国传统数学的重要著作，书中有一道题“今有五雀六燕，集称之衡，雀俱重，燕俱轻；一雀一燕交而处，衡适平；并燕雀重一斤问：燕雀一枚，各重几何？”译文：“五只雀、六只燕，共重斤古时斤两雀重燕轻，互换其中一只，恰好一样重，问：每只雀、燕重量各为多少？”设雀重两，燕重两，可列出方程组A. B.
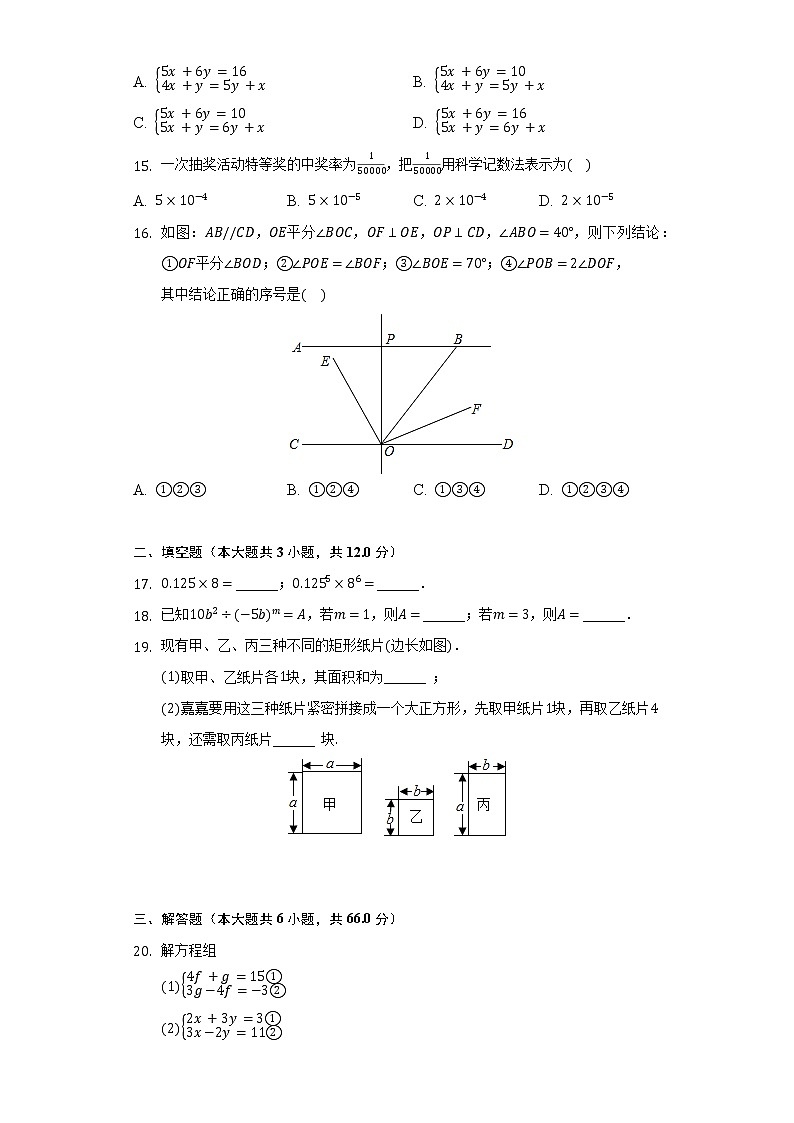
C. D. 一次抽奖活动特等奖的中奖率为，把用科学记数法表示为A. B. C. D. 如图：，平分，，，，则下列结论：
平分；；；，
其中结论正确的序号是
A. B. C. D. 二、填空题（本大题共3小题，共12.0分）______；______．已知，若，则______；若，则______．现有甲、乙、丙三种不同的矩形纸片边长如图．
取甲、乙纸片各块，其面积和为______ ；
嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片块，再取乙纸片块，还需取丙纸片______ 块
三、解答题（本大题共6小题，共66.0分）解方程组

计算：
；
；
先化简，再求值：，其中．

如图，在四边形中，、分别是、延长线上的点，连结，分别交、于点、若，，试说明和．
请完成下面的推理过程，并填空理由或数学式：
______
______
______
______
______
______

______

小红准备完成题目：计算．
她发现第一个因式的一次项系数被墨水遮挡住了．
她把被遮住的一次项系数猜成，请你完成计算：；
老师说：“你猜错了，这个题目的正确答案是不含三次项的．”请通过计算说明原题中被遮住的一次项系数是多少？

为了提倡节约用水，某市制定了两种收费方式：当每户每月用水量不超过时，按一级单价收费；当每户每月用水量超过时，超过部分按二级单价收费已知李阿姨家五月份用水量为，缴纳水费元七月份因孩子放假在家，用水量为，缴纳水费元．
问该市一级水费，二级水费的单价分别是多少？
某户某月缴纳水费为元时，用水量为多少？

小明同学遇到这样一个问题：
如图，已知：，为、之间一点，连接，，得到．
求证：．
小亮帮助小明给出了该问的证明．
证明：
过点作，则有．
，
，
，
．
请你参考小亮的思考问题的方法，解决问题：
直线，直线和直线、分别交于、两点，点、分别在直线、上，
猜想：如图，若点在线段上，，，求的度数．
拓展：如图，若点在直线上，连接、，直接写出、、之间的数量关系．

答案和解析 1.【答案】
【解析】解：：属于二元二次方程，故不符合题意；
符合二元一次方程的定义，故符合题意；
不是整式方程，故不符合题意；
属于二元二次方程，故不符合题意；
符合二元一次方程的定义，故符合题意．
故其中二元一次方程有个．
故选：．
根据二元一次方程的定义作答．含有两个未知数，并且含有未知数的项的次数都是，像这样的整式方程叫做二元一次方程．
本题主要考查二元一次方程的概念，要求熟悉二元一次方程的形式及其特点：含有个未知数，未知数的项的次数是的整式方程．
2.【答案】
【解析】解：．
故选：．
根据零指数幂：，求出的值是多少即可．
此题主要考查了零指数幂的运算，要熟练掌握，解答此题的关键是要明确：；．
3.【答案】
【解析】解：
故选：．
直接利用单项式乘单项式计算得出答案．
此题主要考查了单项式乘单项式，正确掌握相关运算法则是解题关键．
4.【答案】
【解析】解：，
，得，
故选：．
得出，再去括号，合并同类项即可．
本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．
5.【答案】
【解析】解：
，
，
，
故选：．
先求出，再根据平行线的性质得出，代入求出即可．
本题考查了平行线的性质的应用，注意：两直线平行，同位角相等．
6.【答案】
【解析】解：

．
故选：．
首先把、分别化成、，然后应用平方差公式，求出算式的值即可．
此题主要考查了平方差公式的应用，解答此题的关键是要明确：．
7.【答案】
【解析】解：，与是对顶角，
，
平分，
，
．
故选：．
根据对顶角相等求出，再根据角平分线的定义计算的度数，最后根据邻补角的定义得到答案．
本题考查了对顶角、角平分线、邻补角的定义，掌握对顶角相等、邻补角、角平分线的定义是解题的关键．
8.【答案】
【解析】解：，故计算错误；
，故计算正确；
故计算错误；
，故计算错误．
故选：．
利用积的乘方法则逐个计算得结论．
本题考查了整式的运算，掌握积的乘方法则““是解决本题的关键．
9.【答案】
【解析】解：．
故选：．
根据用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的的个数所决定，求解即可得出答案．
本题主要考查了科学记数法，熟练掌握科学记数法表示的方法进行求解是解决本题的关键．
10.【答案】
【解析】解：根据同位角、内错角、同旁内角的概念，可知
第一个图是同位角，第二个图是内错角，第三个图是同旁内角．
故选：．
两条线、被第三条直线所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角；
两个角分别在截线的异侧，且夹在两条被截线之间，具有这样位置关系的一对角互为内错角；
两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角．
据此作答即可．
本题考查了同位角、内错角、同旁内角，解题的关键是掌握同位角、内错角、同旁内角，并能区别它们．
11.【答案】
【解析】解：、，，不符合题意；
B、，，不符合题意；
C、与既不是直线，被任何一条直线所截的一组同位角，内错角，
，不能得到，
符合题意；
D、，，不符合题意；
故选：．
直接用平行线的判定直接判断．
此题是平行线的判定，解本题的关键是熟练掌握平行线的判定定理．
12.【答案】
【解析】【分析】
本题考查了幂的乘方与积的乘方，熟练掌握幂的乘方运算法则是解本题的关键．
先把，，转化为底数为的幂，再根据幂的乘方，底数不变，指数相乘化简．然后根据指数的大小即可比较大小．
【解答】
解：
；
．
则．
故选：．  13.【答案】
【解析】解：由已知可得，
，
解得，
方程组的解为，
故选：．
通过观察所给方程组的关系可得，求出、即可．
本题考查二元一次方程组的解，根据题意得到方程组是解题的关键．
14.【答案】
【解析】解：根据题意，得：
，
故选：．
根据“五只雀、六只燕，共重斤等于两，雀重燕轻．互换其中一只，恰好一样重”，即可得出关于，的二元一次方程组．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
15.【答案】
【解析】解：．
故选：．
本题考查了科学记数法表示绝对值较小的数，掌握科学记数法的表示方法是解题的关键．根据科学记数法表示方法即可求解．
16.【答案】
【解析】解：，，
，
，
平分，
，
故结论正确；
，
，
，
，
，
平分，
故结论正确；
，
，
，
，
故结论正确；
，
，
，
，
，
故结论错误．
故选：．
根据平行线的性质和，由两直线平行，同旁内角互补，可计算出的度数，再根据角平分线的性质，可计算出的度数，根据角平分线的性质可得出的度数，可判断是否正确．根据，由的度数计算出的度数，根据两直线平行，内错角相等的性质，得到的度数，可计算出的度数，可得出结论是否正确，由中的结论可判断是否正确．根据平行线的性质，可得到，可计算出的度数，可得出结论是否正确．
本题主要考查了平行线的性质，合理应用平行线的性质是解决本题关键．
17.【答案】
【解析】解：，
，
故答案为：，．
利用积的乘方的法则进行求解即可．
本题主要考查积的乘方，解答的关键是对积的乘方的法则的掌握与灵活运用．
18.【答案】
【解析】解：当时，

；
当时，

．
故答案为：；．
将的值代入，利用幂的运算性质解得即可．
本题主要考查了整式的除法，正确利用幂的运算性质计算是解题的关键．
19.【答案】；
．
【解析】解：由图可知：一块甲种纸片面积为，一块乙种纸片的面积为，一块丙种纸片面积为，
取甲、乙纸片各块，其面积和为，
故答案为：；
设取丙种纸片块才能用它们拼成一个新的正方形，
是一个完全平方式，
为，
故答案为：．
由图可知：一块甲种纸片面积为，一块乙种纸片的面积为，一块丙种纸片面积为，即可求解；
利用完全平方公式可求解．
本题考查了完全平方式，掌握完全平方公式是解题的关键．
20.【答案】解：，
，得，
解得，
把代入，得，
故原方程组的解为；
，
，得，
解得，
把代入，得，
解得，
故原方程组的解为；
原方程组整理，得，
，得，
解得，
把代入，得，
故原方程组的解为．
【解析】可消去未知数，求出未知数，再把的值代入求出的值即可；
可消去未知数，求出未知数，再把的值代入求出的值即可；
方程组整理后，利用加减消元法求解即可．
本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．
21.【答案】解：

；

；

，
当时，原式．
【解析】先根据多项式乘多项式法则进行计算，再合并同类项即可；
先根据多项式乘多项式进行计算，再合并同类项即可；
先根据完全平方公式，平方差公式，单项式乘多项式进行计算，再合并同类项，最后代入求出答案即可．
本题考查了整式的化简求值，能正确根据整式的运算法则进行化简是解此题的关键，注意运算顺序．
22.【答案】已知对顶角相等等量代换同位角相等，两直线平行两直线平行，同位角相等已知内错角相等，两直线平行
【解析】证明：已知
对顶角相等
等量代换
同位角相等，两直线平行
两直线平行，同位角相等
已知

内错角相等，两直线平行
故答案为：已知；对顶角相等；等量代换；同位角相等，两直线平行；两直线平行，同位角相等；已知；内错角相等，两直线平行．
先根据同位角相等，两直线平行，判定，进而得到，再根据内错角相等，两直线平行，即可得到．
本题主要考查了平行线的判定与性质，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．
23.【答案】解：

；

，
这个题目的正确答案是不含三次项，
，
，
原题中被遮住的一次项系数是．
【解析】根据多项式乘多项式的法则进行解答即可得出答案；
先把被遮住的部分用来代替，再根据多项式乘多项式的法则进行进行计算，然后根据正确答案是不含三次项，得出三次项的和为，从而得出答案．
此题考查了多项式乘多项式，熟练掌握运算法则是解题的关键．
24.【答案】解：设该市一级水费的单价为元，二级水费的单价为元，
依题意得：
解得：．
答：该市一级水费的单价为元，二级水费的单价为元．
元，，
用水量超过．
设用水量为，
依题意得：，
解得：．
答：当缴纳水费为元时，用水量为．
【解析】本题考查了二元一次方程组的应用以及一元一次方程的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；找准等量关系，正确列出一元一次方程．
设该市一级水费的单价为元，二级水费的单价为元，根据“李阿姨家五月份用水量为，缴纳水费元．七月份用水量为，缴纳水费元”，即可得出关于，的二元一次方程组，解之即可得出结论；
求出用水量为时的水费，由该值小于元可得出用水量超过，设用水量为，利用应缴纳水费用水量为时的水费超过的部分，即可得出关于的一元一次方程，解之即可得出结论．
25.【答案】解：猜想：如图，过点作，则，
，
，
，
，
，，
．
拓展：如图，当点在线段上时，
由猜想可知，；
如图，当点在射线上时，
过点作，则，
，
，
，
；
如图，当点在射线上时，
过点作，则，
，
，
，
；
综上所述，、、之间的数量关系为或或．
【解析】猜想：过点作，然后得到，从而得到，，然后得到的度数；
拓展：分情况讨论，当点在线段上时，当点在射线上时，当点在射线上时，然后过点作，再利用平行线的性质进行探究角之间的数量关系．
本题考查了平行线的性质，解题的关键是熟练作出辅助线构造平行线，然后通过平行线的性质得到内错角相等．