
广东省中山市小榄镇2021-2022学年七年级下学期期中数学试卷(含答案)
展开2021-2022学年广东省中山市小榄镇七年级(下)期中数学试卷
一、选择题(本大题10小题,每小題3分,共30分)
1.下列四幅名车标志设计中能用平移得到的是( )
A. 本田
B.奥迪
C.奔驰
D.铃木
2.﹣是的( )
A.相反数 B.倒数 C.绝对值 D.算术平方根
3.点A(,﹣1)在( )象限.
A.第一 B.第二 C.第三 D.第四
4.下列各数中,无理数是( )
A. B.﹣11 C. D.3.1415926
5.将点A(2,﹣3)沿x轴向左平移3个单位长度后得到的点A′的坐标为( )
A.(﹣1,﹣6) B.(2,﹣6) C.(﹣1,﹣3) D.(5,﹣3)
6.对于命题“|a|=a(a为实数)”,能说明它是假命题的反例是( )
A.a=﹣2 B.a=0 C.a= D.a=2
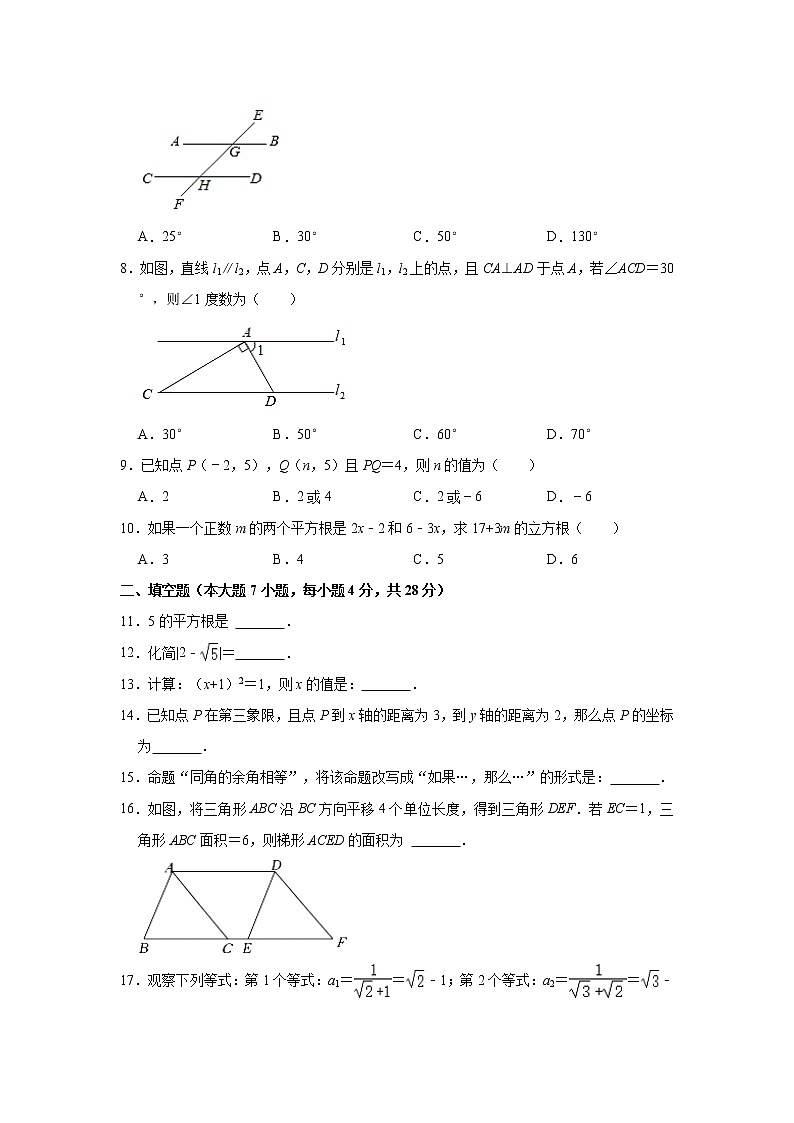
7.如图,AB∥CD,∠EGB=50°,∠CHF=( )
A.25° B.30° C.50° D.130°
8.如图,直线l1∥l2,点A,C,D分别是l1,l2上的点,且CA⊥AD于点A,若∠ACD=30°,则∠1度数为( )
A.30° B.50° C.60° D.70°
9.已知点P(﹣2,5),Q(n,5)且PQ=4,则n的值为( )
A.2 B.2或4 C.2或﹣6 D.﹣6
10.如果一个正数m的两个平方根是2x﹣2和6﹣3x,求17+3m的立方根( )
A.3 B.4 C.5 D.6
二、填空题(本大题7小题,每小题4分,共28分)
11.5的平方根是 .
12.化简|2﹣|= .
13.计算:(x+1)2=1,则x的值是: .
14.已知点P在第三象限,且点P到x轴的距离为3,到y轴的距离为2,那么点P的坐标为 .
15.命题“同角的余角相等”,将该命题改写成“如果…,那么…”的形式是: .
16.如图,将三角形ABC沿BC方向平移4个单位长度,得到三角形DEF.若EC=1,三角形ABC面积=6,则梯形ACED的面积为 .
17.观察下列等式:第1个等式:a1==﹣1;第2个等式:a2==﹣;第3个等式:a3==﹣;…仿照上面等式,写出第n个等式: ;请计算:a1+a2+a3+a4+…+an= .
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.计算:+﹣.
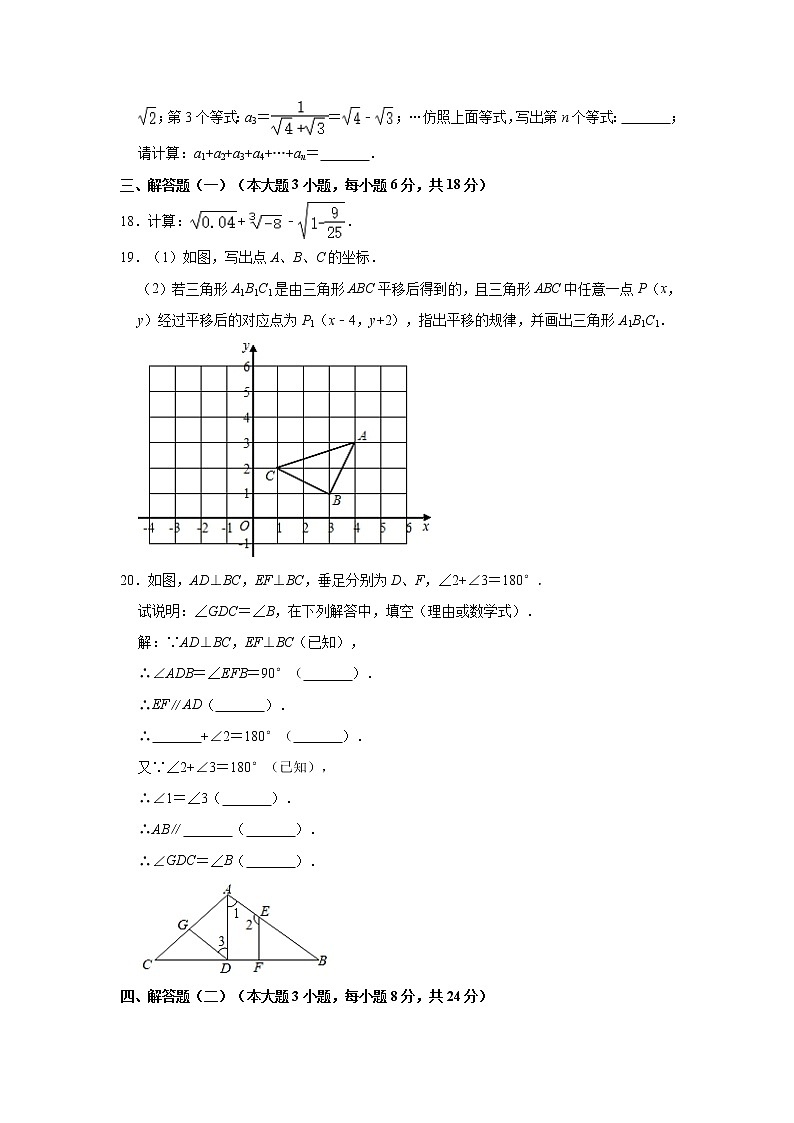
19.(1)如图,写出点A、B、C的坐标.
(2)若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣4,y+2),指出平移的规律,并画出三角形A1B1C1.
20.如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B,在下列解答中,填空(理由或数学式).
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90°( ).
∴EF∥AD( ).
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ).
∴AB∥ ( ).
∴∠GDC=∠B( ).
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.已知点P(8﹣2m,m+1).
(1)若点P在x轴上,求m的值.
(2)若点P的横坐标比纵坐标大4;求出点P的坐标.
22.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
23.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=70°,求∠BAD的度数.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图,长方形ABCD在平面直角坐标系中,其中点B,D坐标分别为(﹣4,﹣4)、(1,2),AD∥x轴,交y轴于M点,AB交x轴于N.
(1)直接写出A,C两点的坐标,并求出长方形ABCD的面积.
(2)一动点P从点A出发,以每秒1个单位长度的速度沿AB边向B点运动,在P点的运动过程中,连接MP,OP,写出∠AMP,∠MPO,∠PON 之间的数量关系?并证明.
(3)在(2)的条件下,是否存在某一时刻t,使得三角形AMP的面积等于长方形ABCD面积的?若存在,求t的值以及此时点P的坐标;若不存在,请说明理由.
25.如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点 E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在射线AG上取一点M(点M在点G下方),使∠ABM=5∠GBM,求证:∠PBM=∠DCH.
参考答案
一、选择题(本大题10小题,每小題3分,共30分)
1.下列四幅名车标志设计中能用平移得到的是( )
A. 本田
B.奥迪
C.奔驰
D.铃木
【分析】根据平移的定义结合图形进行判断.
解:根据平移的定义可知,只有B选项是由一个圆作为基本图形,经过平移得到.
故选:B.
2.﹣是的( )
A.相反数 B.倒数 C.绝对值 D.算术平方根
【分析】根据相反数的定义可解答.
解:﹣是的相反数》
故选:A.
3.点A(,﹣1)在( )象限.
A.第一 B.第二 C.第三 D.第四
【分析】根据平面直角坐标系中的点的坐标特征,即可解答.
解:点A(,﹣1)在第四象限,
故选:D.
4.下列各数中,无理数是( )
A. B.﹣11 C. D.3.1415926
【分析】根据无理数的概念求解即可.
解:A.是分数,属于有理数,故本选项不合题意;
B.﹣11是整数,属于有理数,故本选项不合题意;
C.是无理数,故本选项符合题意;
D.3.1415926是有限小数,属于有理数,故本选项不合题意;
故选:C.
5.将点A(2,﹣3)沿x轴向左平移3个单位长度后得到的点A′的坐标为( )
A.(﹣1,﹣6) B.(2,﹣6) C.(﹣1,﹣3) D.(5,﹣3)
【分析】利用点的平移和点的坐标的变化规律填空即可.
解:点A(2,﹣3)沿x轴向左平移3个单位长度后得到的点A′的坐标为(2﹣3,﹣3),
即(﹣1,﹣3),
故选:C.
6.对于命题“|a|=a(a为实数)”,能说明它是假命题的反例是( )
A.a=﹣2 B.a=0 C.a= D.a=2
【分析】反例就是满足条件,但是不满足结论.根据负数的绝对值等于它的相反数,a取任何一个负数都可以.
解:∵负数的绝对值等于它的相反数,
∴任何一个负数都可以,a=﹣2符合题意,
故选:A.
7.如图,AB∥CD,∠EGB=50°,∠CHF=( )
A.25° B.30° C.50° D.130°
【分析】根据平行线的性质可得∠EHD=∠EGB=50°,再利用对顶角的性质可求解.
解:∵AB∥CD,∠EGB=50°,
∴∠EHD=∠EGB=50°,
∴∠CHF=∠EHD=50°.
故选:C.
8.如图,直线l1∥l2,点A,C,D分别是l1,l2上的点,且CA⊥AD于点A,若∠ACD=30°,则∠1度数为( )
A.30° B.50° C.60° D.70°
【分析】首先根据l1∥l2,可得∠1=∠ADC,再根据∠ACD=30°,CA⊥AD,可得1=60°.
【解答】解∵l1∥l2.
∴∠1=∠ADC.
∵CA⊥AD,∠ACD=30°.
∴∠ADC=90°﹣30°=60°.
∴∠1=60°.
故选:C.
9.已知点P(﹣2,5),Q(n,5)且PQ=4,则n的值为( )
A.2 B.2或4 C.2或﹣6 D.﹣6
【分析】根据点P、Q的纵坐标相等判断出PQ∥x轴,再分点Q在点P的左边与右边两种情况讨论求解.
解:∵点P、Q的纵坐标都是5,
∴PQ∥x轴,
点Q在点P的左边时,n=﹣2﹣4=﹣6,
点Q在点P的右边时,n=﹣2+4=2,
所以,n=2或﹣6.
故选:C.
10.如果一个正数m的两个平方根是2x﹣2和6﹣3x,求17+3m的立方根( )
A.3 B.4 C.5 D.6
【分析】根据平方根、立方根的定义解答即可.
解:由题意,得:
2x﹣2+6﹣3x=0,
解得:x=4.
当x=4时,2x﹣2=6,6﹣3x=﹣6,
m=(±6)2=36.
所以17+3m=17+3×36=125,
所以17+3a的立方根为5.
故选:C.
二、填空题(本大题7小题,每小题4分,共28分)
11.5的平方根是 ± .
【分析】直接根据平方根的定义解答即可.
解:∵(±)2=5,
∴5的平方根是±.
故答案为:±.
12.化简|2﹣|= ﹣2 .
【分析】首先判断(2﹣)的正负情况,然后去绝对值.
解:∵4<5,
∴2<,
∴2﹣<0,
∴|2﹣|=﹣2.
故答案是:﹣2.
13.计算:(x+1)2=1,则x的值是: 0或﹣2 .
【分析】根据平方根的定义即可求出答案.
解:(x+1)2=1,
x+1=±1,
x=0或x=﹣2,
故答案为:0或﹣2.
14.已知点P在第三象限,且点P到x轴的距离为3,到y轴的距离为2,那么点P的坐标为 (﹣2,﹣3) .
【分析】根据第三象限内点的横坐标与纵坐标都是负数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
解:∵点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,
∴x=﹣2,y=﹣3,
∴点P的坐标是(﹣2,﹣3).
故答案为:(﹣2,﹣3).
15.命题“同角的余角相等”,将该命题改写成“如果…,那么…”的形式是: 如果两个角都是同一个角的余角,那么这两个角相等 .
【分析】根据命题写成“如果…,那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论解答.
解:命题“同角的余角相等”,将该命题改写成“如果…,那么…”的形式是:如果两个角都是同一个角的余角,那么这两个角相等.
故答案为:如果两个角都是同一个角的余角,那么这两个角相等.
16.如图,将三角形ABC沿BC方向平移4个单位长度,得到三角形DEF.若EC=1,三角形ABC面积=6,则梯形ACED的面积为 10 .
【分析】由平移的性质得到AD=BE=4,进而求出BC=3,由三角形的面积公式求出h,根据梯形的面积公式即可求出结论.
解:由平移的性质得AD=BE=4,
∵EC=1,
∴BC=BE﹣EC=3
设△ABC的边BC上的高为h,
∵三角形ABC面积=6,
∴BC•h=6,
∴×3h=6,
∴h=4,
∴梯形ACED的面积=(CE+AD)h=(1+4)×4=10,
故答案为:10.
17.观察下列等式:第1个等式:a1==﹣1;第2个等式:a2==﹣;第3个等式:a3==﹣;…仿照上面等式,写出第n个等式: an==﹣ ;请计算:a1+a2+a3+a4+…+an= ﹣1 .
【分析】仿照前面三个等式,即可写出第n个等式,再根据前面已知a1,a2,a3的值和所求出的an的值,进行计算即可解答.
解:仿照上面等式,写出第n个等式:an==﹣;
a1+a2+a3+a4+…+an
=﹣1+﹣+﹣+...+﹣
=﹣1;
故答案为:an==﹣;﹣1.
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.计算:+﹣.
【分析】先计算被开方数,再开方,最后加减.
解:原式=0.2﹣2﹣
=0.2﹣2﹣
=0.2﹣2﹣0.8
=﹣2.6.
19.(1)如图,写出点A、B、C的坐标.
(2)若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣4,y+2),指出平移的规律,并画出三角形A1B1C1.
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可.
解:(1)A(4,3),B(3,1),C(1,2);
(2)如图,三角形A1B1C1即为所求.
20.如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B,在下列解答中,填空(理由或数学式).
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90°( 垂直的定义 ).
∴EF∥AD( 同位角相等两直线平行 ).
∴ ∠1 +∠2=180°( 两直线平行同旁内角互补 ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( 同角的补角相等 ).
∴AB∥ DG ( 内错角相等两直线平行 ).
∴∠GDC=∠B( 两直线平行同位角相等 ).
【分析】根据平行线的判定和性质,垂直的定义,同角的补角相等知识一一判断即可.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.已知点P(8﹣2m,m+1).
(1)若点P在x轴上,求m的值.
(2)若点P的横坐标比纵坐标大4;求出点P的坐标.
【分析】(1)根据x轴上的点纵坐标为0,可得m+1=0,进行计算即可解答;
(2)根据题意可得8﹣2m=m+1+4,从而求出m的值,然后进行计算即可解答.
解:(1)由题意得:
m+1=0,
解得:m=﹣1,
∴m的值为:﹣1;
(2)由题意得:
8﹣2m=m+1+4,
解得:m=1,
∴当m=1时,8﹣2m=6,m+1=2,
∴点P的坐标为(6,2).
22.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
【分析】(1)根据邻补角的概念求出∠BOC,根据角平分线的定义计算,得到答案;
(2)求出∠AOE,根据题意分别求出∠AOF、∠EOF,该解角平分线的定义证明即可.
解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
23.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=70°,求∠BAD的度数.
【分析】(1)由∠1=∠BCE,可得到直线AD与EC平行,可得到∠2与∠4间关系,再由∠2+∠3=180°判断AC与EF的位置关系;
(2)由(1)的结论及垂直可得到∠BAC的度数,再由平行线及角平分线的性质得到∠2的度数,利用角的和差关系可得结论.
解:(1)AC∥EF.理由如下:
∵∠1=∠BCE,
∴AD∥CE,
∴∠2=∠4,
∵∠2+∠3=180°,
∴∠4+∠3=180°,
∴EF∥AC;
(2)∵AD∥EC,CA平分∠BCE,
∴∠ACD=∠4=∠2,
∵∠1=70°,∠1=∠2+∠ACD,
∴∠2=35°,
∵EF∥AC,EF⊥AB于F,
∴∠BAC=∠F=90°,
∴∠BAD=∠BAC﹣∠2=55°.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图,长方形ABCD在平面直角坐标系中,其中点B,D坐标分别为(﹣4,﹣4)、(1,2),AD∥x轴,交y轴于M点,AB交x轴于N.
(1)直接写出A,C两点的坐标,并求出长方形ABCD的面积.
(2)一动点P从点A出发,以每秒1个单位长度的速度沿AB边向B点运动,在P点的运动过程中,连接MP,OP,写出∠AMP,∠MPO,∠PON 之间的数量关系?并证明.
(3)在(2)的条件下,是否存在某一时刻t,使得三角形AMP的面积等于长方形ABCD面积的?若存在,求t的值以及此时点P的坐标;若不存在,请说明理由.
【分析】(1)利用点A、C的坐标和矩形的性质易得B(﹣4,﹣4),D(1,2),然后根据矩形面积公式计算矩形ABCD的面积;
(2)分类讨论:当点P在线段AN上时,作PQ∥AM,如图,利用平行线的性质易得∠QPM=∠AMP,∠QPO=∠PON,则∠MPO=∠AMP+∠PON;当点P在线段NB上时,同样方法可得∠MPO=∠AMP﹣∠PON;
(3)由于AM=4,AP=t,根据三角形面积公式得到S△AMP=2t,再利用三角形AMP的面积等于长方形面积的可计算出t=5,则AP=5,然后根据点的坐标的表示方法写出P点坐标.
解:(1)∵点B、D坐标分别为(﹣4,﹣4)、(1,2),
而四边形ABCD为矩形,
∴A(﹣4,2),C(1,﹣4);
∴矩形ABCD的面积=(1+4)×(2+4)=30;
(2)当点P在线段AN上时,作PQ∥AM,如图,
∵AM∥ON,
∴AM∥PQ∥ON,
∴∠QPM=∠AMP,∠QPO=∠PON,
∴∠QPM+∠QPO=∠AMP+∠PON,
即∠MPO=∠AMP+∠PON;
当点P在线段NB上时,同样方法可得∠MPO=∠AMP﹣∠PON;
(3)存在.
∵AM=4,AP=t,
∴S△AMP=×4×t=2t,
∵三角形AMP的面积等于长方形面积的,
∴2t=30×=10,
∴t=5
∴AP=5,
∵AN=2,
∴P点坐标为(﹣4,﹣3).
25.如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点 E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在射线AG上取一点M(点M在点G下方),使∠ABM=5∠GBM,求证:∠PBM=∠DCH.
【分析】(1)由AD∥BC,得∠GAD=∠BGA,又AG平分∠BAD,有∠BAG=∠GAD,故∠BAG=∠BGA;
(2)CF平分∠BCD,∠BCD=90°,知∠GCF=45°,而AD∥BC,有∠AEF=∠GCF=45°,根据∠ABG=50°,得∠DAB=180°﹣50°=130°,又AG平分∠BAD,得∠BAG=∠GAD=65°,即得∠AFC=65°﹣45°=20°;
(3)根据平行线的性质、三角形外角性质、角的和差即可得解.
【解答】(1)证明:∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD,
∴∠BAG=∠BGA;
(2)解:∵CF平分∠BCD,∠BCD=90°,
∴∠GCF=45°,
∵AD∥BC,
∴∠AEF=∠GCF=45°,∠DAB+∠ABG=180°,
∵∠ABG=50°,
∴∠DAB=180°﹣50°=130°,
∵AG平分∠BAD,
∴∠BAG=∠GAD=65°,
∵∠GAD=∠AFC+∠AEF,
∴∠AFC=65°﹣45°=20°;
(3)证明:设∠ABC=4x,
∵∠ABP=3∠PBG,∠ABP+∠PBG=∠ABC,
∴∠ABP=3x,∠PBG=x,
由(1)知,∠BAG=∠BGA,
∵AG∥CH,
∴∠BCH=∠AGB==90°﹣2x,
∵∠BCD=90°,
∴∠DCH=90°﹣(90°﹣2x)=2x,
∴∠ABM=∠ABP+∠PBG+∠GBM=3x+x+∠GBM=4x+∠GBM,
∵∠ABM=5∠GBM,
∴∠GBM=x,
∴∠PBM=∠PBG+∠GBM=2x,
∴∠PBM=∠DCH.
广东省中山市小榄镇2023-2024学年八年级上学期期中考试数学试题: 这是一份广东省中山市小榄镇2023-2024学年八年级上学期期中考试数学试题,文件包含广东省中山市小榄镇2023-2024学年八年级上学期期中考试数学试题docx、广东省中山市小榄镇2023-2024学年八年级上学期期中考试数学答案docx等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
广东省中山市小榄镇2023-2024年九年级上学期期中数学试题: 这是一份广东省中山市小榄镇2023-2024年九年级上学期期中数学试题,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省中山市小榄镇2023-2024学年七年级上学期数学期中试卷: 这是一份广东省中山市小榄镇2023-2024学年七年级上学期数学期中试卷,共4页。












