


2022新高考数学临考押题卷及答案解析(三)
展开2022年高考临考押题卷(三)
数学(新高考卷)
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、 单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
1.设集合,则( )
A. B. C. D.
2.已知复数z满足.则( )
A.1 B.2 C. D.
3.如图1,在高为h的直三棱柱容器中,,.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为(如图2),则容器的高h为( )
A.3 B.4 C. D.6
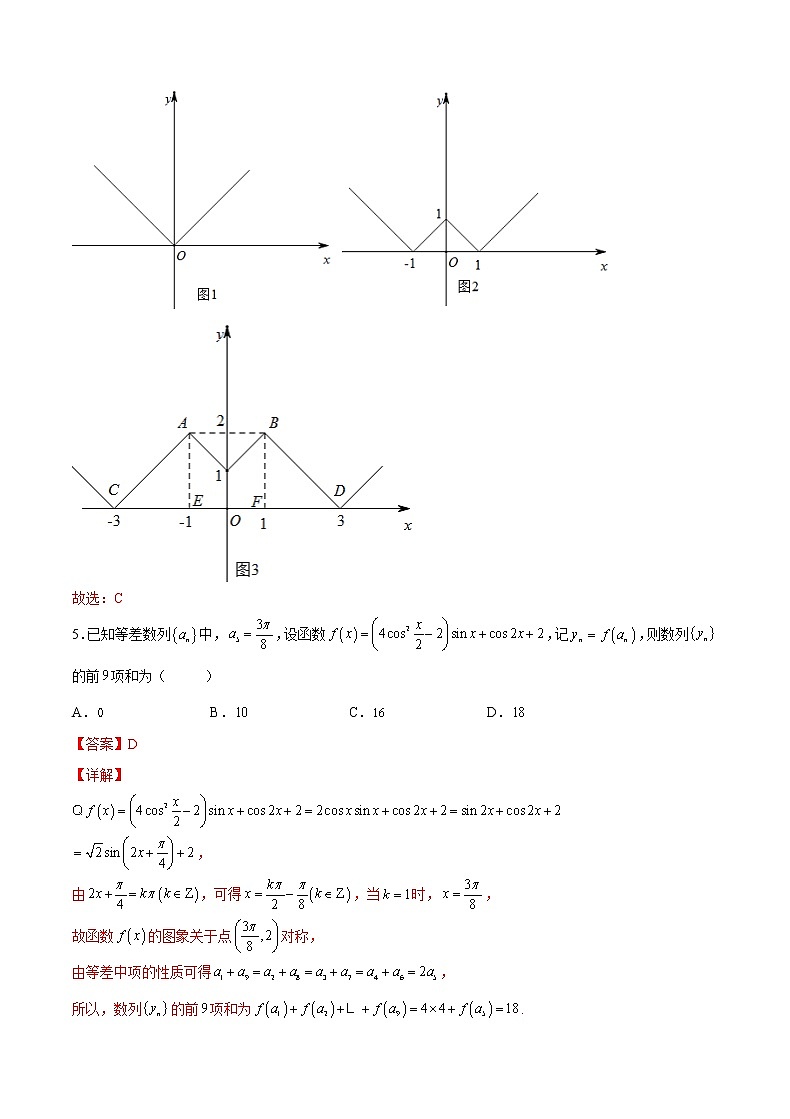
4.设函数,,,则函数的图象与轴所围成图形中的封闭部分面积是( )
A.6 B.8 C.7 D.9
5.已知等差数列中,,设函数,记,则数列的前项和为( )
A. B. C. D.
6.过抛物线焦点F的直线与该抛物线及其准线都相交,交点从左到右依次为A,B,C.若,则线段BC的中点到准线的距离为( )
A.3 B.4 C.5 D.6
7.如图为一个直角三角形工业部件的示意图,现在AB边内侧钻5个孔,在BC边内侧钻4个孔,AB边内侧的5个孔和BC边内侧的4个孔可连成20条线段,在这些线段的交点处各钻一个孔,则这个部件上最多可以钻的孔数为( ).
A.190 B.199 C.69 D.60
8.已知函数,直线是曲线的一条切线,则的取值范围是( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.已知向量,将向量绕坐标原点逆时针转角得到向量,则下列说法正确的是( )
A. B.
C. D.
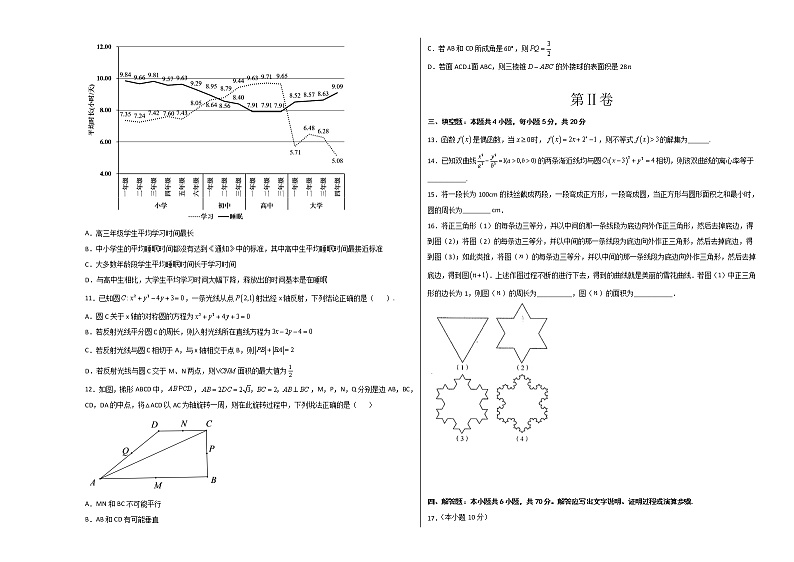
10.睡眠很重要,教育部《关于进一步加强中小学生睡眠管理工作的通知》中强调“小学生每天睡眠时间应达到10小时,初中生应达到9小时,高中生应达到8小时”.某机构调查了1万个学生时间利用信息得出下图,则以下判断正确的有( )
A.高三年级学生平均学习时间最长
B.中小学生的平均睡眠时间都没有达到《通知》中的标准,其中高中生平均睡眠时间最接近标准
C.大多数年龄段学生平均睡眠时间长于学习时间
D.与高中生相比,大学生平均学习时间大幅下降,释放出的时间基本是在睡眠
11.已知圆,一条光线从点射出经x轴反射,下列结论正确的是( ).
A.圆C关于x轴的对称圆的方程为
B.若反射光线平分圆C的周长,则入射光线所在直线方程为
C.若反射光线与圆C相切于A,与x轴相交于点B,则
D.若反射光线与圆C交于M、N两点,则面积的最大值为
12.如图,梯形ABCD中,,,M,P,N,Q分别是边AB,BC,CD,DA的中点,将△ACD以AC为轴旋转一周,则在此旋转过程中,下列说法正确的是( )
A.MN和BC不可能平行
B.AB和CD有可能垂直
C.若AB和CD所成角是,则
D.若面ACD⊥面ABC,则三棱锥的外接球的表面积是28π
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分
13.函数是偶函数,当时,,则不等式的解集为______.
14.已知双曲线的两条渐近线均与圆相切,则该双曲线的离心率等于___________.
15.将一段长为100cm的铁丝截成两段,一段弯成正方形,一段弯成圆,当正方形与圆形面积之和最小时,圆的周长为________ cm.
16.将正三角形(1)的每条边三等分,并以中间的那一条线段为底边向外作正三角形,然后去掉底边,得到图(2);将图(2)的每条边三等分,并以中间的那一条线段为底边向外作正三角形,然后去掉底边,得到图(3);如此类推,将图()的每条边三等分,并以中间的那一条线段为底边向外作三角形,然后去掉底边,得到图.上述作图过程不断的进行下去,得到的曲线就是美丽的雪花曲线.若图(1)中正三角形的边长为1,则图()的周长为__________,图()的面积为___________.
四、解答题:本小题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)
已知是数列的前项和,,___________.
①,;②数列为等差数列,且的前项和为.从以上两个条件中任选一个补充在横线处,并求解:
(1)求;
(2)设,求数列的前项和.
18.(本小题12分)
羽毛球看似小巧,但羽毛球运动却有着丰富的文化内涵,简洁的场地、几个人的组合,就可以带来一场充满乐趣、斗智斗勇、健身休闲的竞技比赛,参与者可以根据自己的年龄、性别、身体条件、技术水平,选择适合自己的运动强度和竞技难度.小胡和小李两名员工经常利用业余时间进行羽毛球比赛,规定每一局比赛中获胜方记1分,失败方记0分,没有平局,谁先获得5分就获胜,比赛结束,假设每局比赛小胡获胜的概率都是,各局比赛的结果相互独立.
(1)求比赛结束时恰好打了6局的概率;
(2)若现在是小胡的比分落后,记表示结束比赛还需打的局数,求的分布列及数学期望.
19.(本小题12分)
在中,角的对边分别,.
(1)求;
(2)若的周长为4,面积为,求.
20.(本小题12分)
如图,在三棱锥中,平面平面,,为的中点.
(1)证明:;
(2)已知是边长为1的等边三角形,且三棱锥的体积为,若点在棱
21.(本小题12分)
已知椭圆的离心率为,且点在椭圆上.
(1)求椭圆的方程;
(2)若四边形的顶点在椭圆上,且对角线过原点,直线和的斜率之积为,证明:四边形的面积为定值.
22.(本小题12分)
已知函数,曲线在点处的切线方程为.
(1)求,的值;
(2)若,是两个正数,且,证明:.
2022新高考数学临考押题卷及答案解析(五): 这是一份2022新高考数学临考押题卷及答案解析(五),文件包含临考押题卷05解析版docx、临考押题卷05考试版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
2022新高考数学临考押题卷及答案解析(一): 这是一份2022新高考数学临考押题卷及答案解析(一),文件包含临考押题卷01解析版docx、临考押题卷01考试版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
2022新高考数学临考押题卷及答案解析(六): 这是一份2022新高考数学临考押题卷及答案解析(六),文件包含临考押题卷06解析版docx、临考押题卷06考试版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。












