2022新高考数学临考押题卷及答案解析（一）

这是一份2022新高考数学临考押题卷及答案解析（一），文件包含临考押题卷01解析版docx、临考押题卷01考试版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
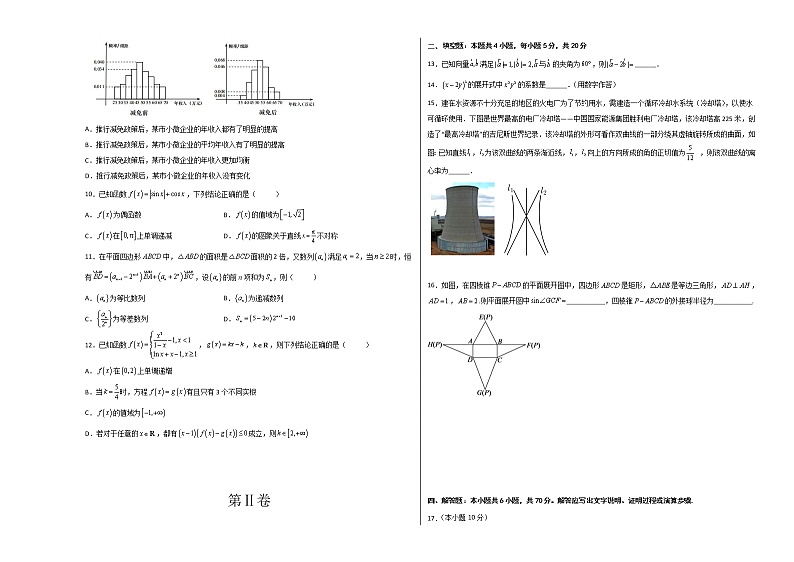
2022年高考临考押题卷（一）数学（新高考卷）（考试时间：120分钟  试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。4．考试结束后，将本试卷和答题卡一并交回。一、 单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.1．已知全集，，则（       ）A． B． C． D．【答案】B【详解】由题意，全集，且，根据集合补集的概念及运算，可得.故选：B.2．复数满足，则（       ）A． B． C．2 D．【答案】A【详解】因为，所以，所以.故选：A3．已知，则的值为（       ）A． B． C． D．【答案】A【详解】因，所以.故选：A4．甲乙两选手进行象棋比赛，已知每局比赛甲获胜的概率为0.6，乙获胜的概率为0.4，若采用三局二胜制，则甲最终获胜的概率为（       ）A．0.36 B．0.352 C．0.288 D．0.648【答案】D【详解】由题意可得甲最终获胜有两种情况：一是前两局甲获胜，则获胜的概率为二是前两局甲胜一局，第三局甲获胜，则获胜的概率为，而这两种情况是互斥的，所以甲最终获胜的概率为，故选：D5．已知抛物线C：（）的焦点为F，点M在抛物线C上，射线FM与y轴交于点，与抛物线C的准线交于点N，，则p的值等于（       ）A． B．2 C． D．4【答案】B【详解】解：设点M到抛物线的准线的距离为|MM′|，抛物线的准线与x轴的交点记为点B. 由抛物线的定义知，|MM′|＝|FM|.因为，所以，即，所以，而，解得p＝2,故选：B.6．某品牌暖水瓶的内胆规格如图所示，分为①②③④四个部分（水瓶内胆壁厚不计），它们分别为一个半球，一个大圆柱，一个圆台和一个小圆柱．若其中圆台部分的体积为cm3，且水瓶灌满水后盖上瓶塞时水溢出cm3，则盖上瓶塞后水瓶的最大盛水量为（            ）A．cm3 B．cm3 C．cm3 D．cm3【答案】A【详解】半球体积，大圆柱的体积，圆台的体积，小圆柱的体积，所以最大盛水量为.故选：A7．在如今这个5G时代，6G研究已方兴未艾．2021年8月30日第九届未来信息通信技术国际研讨会在北京举办．会上传出消息，未来6G速率有望达到1Tbps，并启用毫米波、太赫兹、可见光等尖端科技，有望打造出空天地融合的立体网络，预计6G数据传输速率有望比5G快100倍，时延达到亚毫秒级水平．香农公式是被广泛公认的通信理论基础和研究依据，它表示：在受噪声干扰的信道中，最大信息传递率C取决于信道带宽W、信道内信号的平均功率S，信道内部的高斯噪声功率N的大小，其中叫做信噪比．若不改变带宽W，而将信噪比从11提升至499，则最大信息传递率C会提升到原来的（       ）参考数据： ．A．2.4倍 B．2.5倍 C．2.6倍 D．2.7倍【答案】B【详解】设提升前最大信息传递率为，提升后最大信息传递率为，则由题意可知，，，所以倍.所以最大信息传递率C会提升到原来的倍.故选：B.8．已知函数有两个不同的极值点，且不等式恒成立，则实数t的取值范围是（       ）A． B． C． D．【答案】A【详解】，因为函数有两个不同的极值点，，所以方程有两个不相等的正实数根，于是有，解得.因为不等式恒成立，所以恒成立.，设，，故在上单调递增，故，所以.因此实数t的取值范围是.故选：A二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.9．某市为了更好的支持小微企业的发展，对全市小微企业的年税收进行适当的减免，为了解该地小微企业年收入的变化情况，对该地小微企业减免前和减免后的年收入进行了抽样调查，将调查数据整理，得到如下所示的频率分布直方图，则下列结论正确的是（       ）A．推行减免政策后，某市小微企业的年收入都有了明显的提高B．推行减免政策后，某市小微企业的平均年收入有了明显的提高C．推行减免政策后，某市小微企业的年收入更加均衡D．推行减免政策后，某市小微企业的年收入没有变化【答案】BC【详解】对于A从图中无法确定推行减免政策后，某市小微企业的年收入是否都有了明显的提高，故A错误，对于B从图中可以看出，减免前占比最多的平均年收入为万元，其次是万元及万元，减免后占比最多的为万元，其次是万元及万元，明显增多，所以平均年收入也有明显提高，B正确.对C，从图中看出，推行减免政策后，年收入的中位数是，而减免前年收入的中位数是，所以减免后年收入更加均衡，所以C错误对于 D从图中看出，某市小微企业的年收入有明显变化，所以D错误.故选:BC10．已知函数，下列结论正确的是（       ）A．为偶函数 B．的值域为C．在上单调递减 D．的图象关于直线不对称【答案】AB【详解】对于A：因为的定义域为R，且，所以函数是偶函数，即选项A正确；对于B：由题意，得，即，当时，，则，即；当时，，则，即；综上所述，的值域为，即选项B正确；对于C：当时，，且，令，得，令，得，即在上单调递增，在上单调递减，即选项C错误；对于D：由选项B得的最大值为，且，即的图象关于直线对称，即选项D错误.故选：AB.11．在平面四边形ABCD中，的面积是面积的2倍，又数列满足，当时，恒有，设的前n项和为，则（       ）A．为等比数列 B．为递减数列C．为等差数列 D．【答案】BCD【详解】设与交于点，，，共线，所以存在实数，使得，所以，所以，所以，，所以，，，不是等比数列，A错；因为，所以，即，所以是等差数列，C正确；又因为，则，即，，所以当时，，即，所以是递减数列，B正确；因为，，所以两式相减得，所以，D正确．故选：BCD．12．已知函数，，，则下列结论正确的是（       ）A．在上单调递增B．当时，方程有且只有3个不同实根C．的值域为D．若对于任意的，都有成立，则【答案】BCD【解析】【详解】对于A：.因为，，所以，所以.所以在上不是增函数.故A错误；对于B：当时，方程可化为：或.由可解得：.对于，显然代入方程成立，所以是方程的根.当时，记..所以令，解得：；令，解得：；所以在上单增，在上单减.所以.所以在上没有零点；而在上单减，且，，所以在上有且只有一个零点.综上所述：当时，方程有且只有3个不同实根.故B正确；对于C：对于.当时，.，所以；当时，..令，解得：；令，解得：；所以在上单减，在上单增.所以；故的值域为成立.故C正确.对于D：对于任意的，都有成立，所以及恒成立.若恒成立，则有.令，只需.令，则.则.所以，即.若恒成立，当，无论k取何值，不等式均成立，所以.当，则有.令，只需..记，则，所以在上单减，所以，即，所以在上单减，所以所以.综上所述：.故D正确.故选：BCD二、 填空题：本题共4小题，每小题5分，共20分13．已知向量满足与的夹角为，则______．【答案】【详解】根据题意，，又，则.故答案为：．14．的展开式中的系数是______．（用数字作答）【答案】【详解】的展开式的通项公式为，令可得所以的展开式中的系数是故答案为：15．建在水资源不十分充足的地区的火电厂为了节约用水，需建造一个循环冷却水系统（冷却塔），以使水可循环使用．下图是世界最高的电厂冷却塔——中国国家能源集团胜利电厂冷却塔，该冷却塔高225米，创造了“最高冷却塔”的吉尼斯世界纪录．该冷却塔的外形可看作双曲线的一部分绕其虚轴旋转所成的曲面，如图：已知直线，为该双曲线的两条渐近线，，向上的方向所成的角的正切值为，则该双曲线的离心率为______． 【答案】【详解】解：设一条渐近线向上的方向与虚轴向上的方向所成的角为，则，解得或（舍），即，故，所以．故答案为：.16．如图，在四棱锥的平面展开图中，四边形ABCD是矩形，是等边三角形，，，.则平面展开图中___________，四棱锥的外接球半径为___________. 【答案】     ##     ##【详解】因为在四棱锥的平面展开图中，四边形ABCD是矩形，是等边三角形，，，，所以，所以，，，如图，连接交于点，四棱锥的外接球球心为，在四棱锥中，，，所以平面，因为平面，所以平面平面，取的中点，连接，因为为等边三角形，所以，因为平面平面，平面，所以平面，设的外接圆圆心为，连接，则平面，平面，则∥，可证得∥，所以四边形是矩形，连接，由于为等边三角形，所以，所以,设四棱锥的外接球半径为，则，解得，故答案为：，17．已知是公差为2的等差数列，，且是和的等比中项．(1)求的通项公式；(2)设数列满足，求的前n项和．【答案】(1)(2)【解析】(1)依题意，是公差为2的等差数列，，且是和的等比中项，即，即，所以.(2)依题意①，当时，，当时，②，①-②得：，所以.③，④，③-④得：，所以.18．已知的内角、、的对边分别为、、，且的面积为．(1)求；(2)若，的角平分线与边相交于点，延长至点，使得，求．【答案】(1)(2)【解析】(1)解：由题可知，所以，由余弦定理，所以，可得，因为，所以.(2)解：不妨令，因为，可得，，又因为为的角平分线，所以，，得，所以在中，由余弦定理可得，即，在中，可得，，所以，为等边三角形，所以，在中，由余弦定理可得，得．19．如图①，在梯形中，，，，为的中点，以为折痕把折起，连接，，得到如图②的几何体，在图②的几何体中解答下列两个问题．(1)证明：；(2)请从以下两个条件中选择一个作为已知条件，求二面角的余弦值．①四棱锥的体积为2；②直线与所成角的余弦值为．注：如果选择两个条件分别解答，按第一个解答计分．【解析】(1)证明：在图①中因为，，为中点所以，，所以为平行四边形，所以，同理可证，在图②中，取中点，连接，，，因为，所以，，因为，所以平面，因为平面，所以.(2)若选择①：因为平面，平面，所以平面平面且交线为，所以过点作，则平面，因为，所以四棱锥的体积，所以，所以与重合，所以平面，建系如图，则，，， ，平面法向量为，设平面法向量为，因为，，所以，得，设二面角的大小为，则，所以二面角的余弦值为.若选择②：因为，所以即为异面直线与所成角，在中，，所以所，以，所以，因为平面，平面，所以平面平面且交线为，所以平面，建系如图，则，，， ，平面法向量为，设平面法向量为，因为，，所以，得，设二面角的大小为，则，所以二面角的余弦值为.20．第56届世界乒乓球锦标赛将于2022年在中国成都举办，国球运动又一次掀起热潮.现有甲乙两人进行乒乓球比赛，比赛采用7局4胜制，每局为11分制，每赢一球得1分.(1)已知某局比赛中双方比分为8：8，此时甲先连续发球2次，然后乙连续发球2次，甲发球时甲得分的概率为，乙发球时乙得分的概率为，各球的结果相互独立，求该局比赛甲以11：9获胜的概率；(2)已知在本场比赛中，前两局甲获胜，在后续比赛中，每局比赛甲获胜的概率为，乙获胜的概率为，且每局比赛的结果相互独立.两人又进行了X局后比赛结束，求X的分布列与数学期望.【答案】(1)(2)见解析，【解析】(1)解：设事件“在比分为8：8的条件下甲以11：9获胜”，则.(2)解：随机变量X的所有可能取值为：2，3，4，5，，，，，所以随机变量X的分布列为：X2345P 所以.21．已知椭圆C：（）的左，右焦点分别为，，上，下顶点分别为A，B，四边形的面积和周长分别为2和.(1)求椭圆C的方程；(2)若直线l：（）与椭圆C交于E，F两点，线段EF的中垂线交y轴于M点，且为直角三角形，求直线l的方程.【答案】(1)(2)或【解析】(1)由题意知，解得故椭圆的方程为(2)设联立，整理得由韦达定理得，，，所以线段EF的中垂线方程为，令，解得，，，又为直角三角形，且，，即所以直线l的方程或22．已知函数（其中a为参数）．(1)求函数的单调区间；(2)若对任意都有成立，求实数a的取值集合；(3)证明：（其中，e为自然对数的底数）．【解析】(1)解：因为函数，定义域为，所以，当时，，函数在上递增；当时，令，得，当时，，函数在上递减；当时，，函数在上递增； 所以当时，函数的单调增区间是，无减区间；当时，函数的单调增区间是，减区间是；(2)当时，在上递增，又，当时，，所以不成立；当时，由（1）得，因为对任意都有成立，所以，令，则，令，得，当时，，当时，，所以当时，取得最大值，所以实数a的取值集合是；(3)由（2）知：，令，则，即，则，所以，由（2）知：，令，则，即，则，所以，故.