高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系导学案

这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系导学案，共9页。
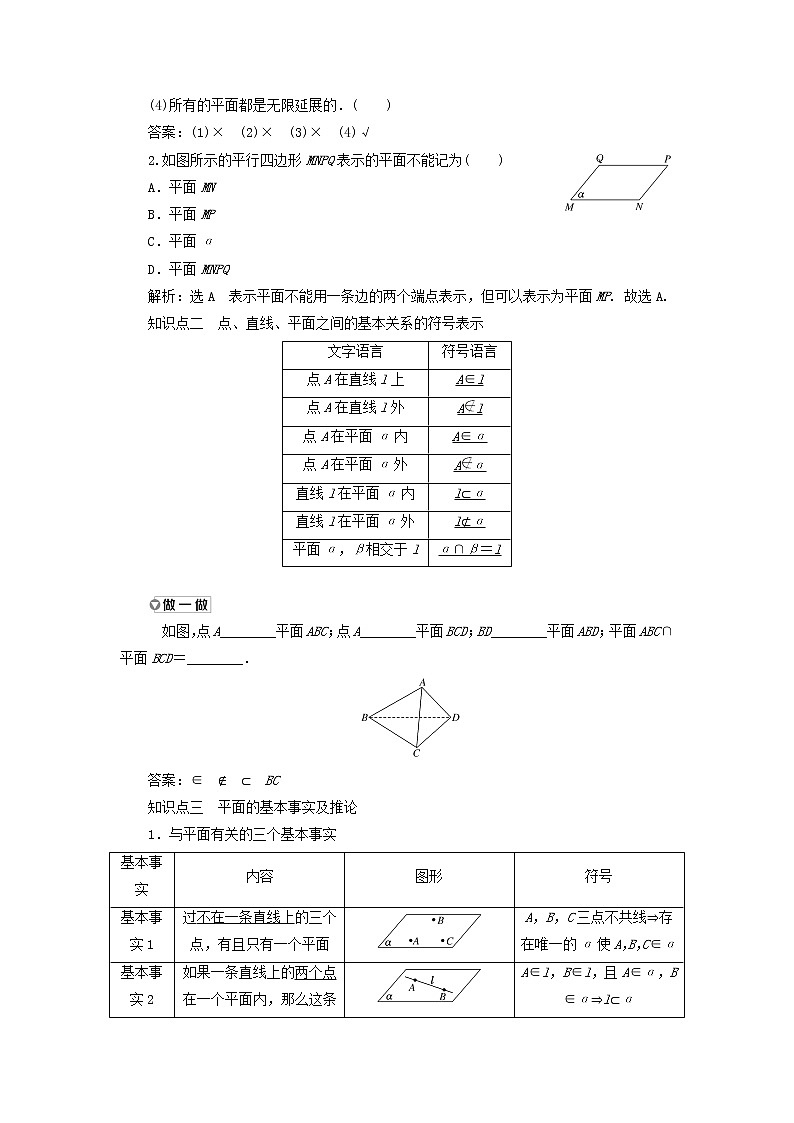
平面新课程标准解读核心素养1.借助日常生活中的实物，在直观认识空间点、直线、平面的基础上，抽象出空间点、直线、平面的概念数学抽象，直观想象2.了解基本事实和确定平面的推论逻辑推理在生活中，用两个合页和一把锁就可以将一扇门固定，将一把直尺置于桌面上，通过是否漏光就能检查桌面是否平整．[问题]　你知道如此做的原理吗？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　知识点一　平面的画法与表示1．平面的画法画法我们常用矩形的直观图，即平行四边形表示平面当平面水平放置时，常把平行四边形的一边画成横向当平面竖直放置时，常把平行四边形的一边画成竖向图示2．平面的表示方法(1)用希腊字母表示，如平面α，平面β，平面γ；(2)用代表平面的平行四边形的四个顶点的大写英文字母表示，如平面ABCD；(3)用代表平面的平行四边形的相对的两个顶点的大写英文字母表示，如平面AC，平面BD.1．判断正误．(正确的画“√”，错误的画“×”)(1)书桌面是平面．(　　)(2)8个平面重叠起来要比6个平面重叠起来厚．(　　)(3)一个平面的面积是16 cm2.(　　)(4)所有的平面都是无限延展的．(　　)答案：(1)×　(2)×　(3)×　(4)√2.如图所示的平行四边形MNPQ表示的平面不能记为(　　)A．平面MNB．平面MPC．平面αD．平面MNPQ解析：选A　表示平面不能用一条边的两个端点表示，但可以表示为平面MP. 故选A.知识点二　点、直线、平面之间的基本关系的符号表示文字语言符号语言点A在直线l上A∈l点A在直线l外Al点A在平面α内A∈α点A在平面α外Aα直线l在平面α内l⊂α直线l在平面α外l⊄α平面α，β相交于lα∩β＝l 　如图，点A________平面ABC；点A________平面BCD；BD________平面ABD；平面ABC∩平面BCD＝________．答案：∈　∉　⊂　BC知识点三　平面的基本事实及推论1．与平面有关的三个基本事实基本事实内容图形符号基本事实1过不在一条直线上的三个点，有且只有一个平面A，B，C三点不共线⇒存在唯一的α使A，B，C∈α基本事实2如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内A∈l，B∈l，且A∈α，B∈α⇒l⊂α基本事实3如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线P∈α，且P∈β⇒α∩β＝l，且P∈l2．基本事实1、2的三个推论推论内容图形作用推论1经过一条直线和这条直线外一点，有且只有一个平面确定平面的依据推论2经过两条相交直线，有且只有一个平面推论3经过两条平行直线，有且只有一个平面1．如何理解基本事实1中的“有且只有一个”？提示：这里的“有”是说图形存在，“只有一个”是说图形唯一，本公理强调的是存在性和唯一性两个方面，因此“有且只有一个”，必须完整地使用，不能仅用“只有一个”来代替“有且只有一个”，否则就没有表达存在性．确定一个平面中的“确定”是“有且只有一个”的同义词，也就是存在性和唯一性这两个方面的，这个术语今后学习中会经常出现．2．两个不重合的平面可能存在有限个公共点吗？提示：不能．要么没有公共点，要么有无数个公共点．3．如果两个不重合的平面有无数个公共点，那么这些公共点有什么特点？提示：这些公共点落在同一条直线上．立体几何三种语言的相互转化[例1]　用符号表示下列语句，并画出图形：(1)平面α与β相交于直线l，直线a与α，β分别相交于点A，B；(2)点A，B在平面α内，直线a与平面α交于点C，点C不在直线AB上．[解]　(1)用符号表示：α∩β＝l，a∩α＝A，a∩β＝B，如图．(2)用符号表示：A∈α，B∈α，a∩α＝C，C∈/AB，如图．三种语言的转换方法(1)用文字语言、符号语言表示一个图形时，首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何，试着用文字语言表示，再用符号语言表示；(2)要注意符号语言的意义，如点与直线的位置关系只能用“∈”或“∉”，直线与平面的位置关系只能用“⊂”或“⊄”．[提醒]　根据符号语言或文字语言画相应的图形时，要注意实线和虚线的区别．　　　　 [跟踪训练]根据图形用符号表示下列点、直线、平面之间的关系：(1)点P与直线AB；(2)点C与直线AB；(3)点M与平面AC；(4)点A1与平面AC；(5)直线AB与直线BC；(6)直线AB与平面AC；(7)平面A1B与平面AC.解：(1)点P∈直线AB；(2)点C ∉直线AB；(3)点M∈平面AC；(4)点A1∉平面AC；(5)直线AB∩直线BC＝点B；(6)直线AB⊂平面AC；(7)平面A1B∩平面AC＝直线AB.点、线共面问题[例2]　如图，已知直线a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C.求证：直线a，b，c和l共面．[证明]　法一(辅助平面法)：因为a∥b，所以a，b确定一个平面α.因为A∈a，B∈b，所以A∈α，B∈α.又A∈l，B∈l，所以l⊂α.因为C∈l，所以C∈α，所以直线a与点C同在平面α内．因为a∥c，所以直线a，c确定一个平面β.因为C∈c，c⊂β，所以C∈β，即直线a与点C同在平面β内．由推论1，可得平面α和平面β重合，则c⊂α.所以a，b，c，l共面．法二(纳入平面法)：因为a∥b，所以a，b确定一个平面α.因为A∈a，B∈b，所以A∈α，B∈α.又A∈l，B∈l，所以l⊂α.则a，b，l都在平面α内，即b在a，l确定的平面内．同理可证c在a，l确定的平面内．因为过a与l只能确定一个平面，所以a，b，c，l共面于a，l确定的平面．证明点、线共面的方法证明点、线共面的主要依据是基本事实1、基本事实2及其推论，常用的方法有：(1)辅助平面法，先证明有关点、线确定平面α，再证明其余点、线确定平面β，最后证明平面α，β重合；(2)纳入平面法，先由条件确定一个平面，再证明有关的点、线在此平面内．　　　　 [跟踪训练]已知A∈l，B∈l，C∈l，D∉l，如图．求证：直线AD，BD，CD共面．证明：因为直线l与点D可以确定平面α，所以只需证明AD，BD，CD都在平面α内．因为D∉l，所以l与D可以确定平面α.因为A∈l，所以A∈α.又D∈α，所以AD⊂α.同理，BD⊂α，CD⊂α，所以AD，BD，CD在同一平面α内，即它们共面.点共线、线共点问题[例3]　如图所示，在正方体ABCD­A1B1C1D1中，E，F分别为AB，AA1的中点．求证：CE，D1F，DA三线交于一点．[证明]　如图，连接EF，D1C，A1B，因为E为AB的中点，F为AA1的中点，所以EF綉A1B.又因为A1B綉D1C，所以EF綉D1C，所以E，F，D1，C四点共面，可设D1F∩CE＝P.又D1F⊂平面A1D1DA，CE⊂平面ABCD，所以点P为平面A1D1DA与平面ABCD的公共点．又因为平面A1D1DA∩平面ABCD＝DA，所以据基本事实3可得P∈DA，即CE，D1F，DA三线交于一点．[母题探究](变条件、变设问)若将本例条件中的“E，F分别为AB，AA1的中点”改成“E，F分别为AB，AA1上的点，且D1F∩CE＝M”，求证：点D，A，M三点共线．证明：因为D1F∩CE＝M，且D1F⊂平面A1D1DA，所以M∈平面A1D1DA，同理M∈平面BCDA，从而M在两个平面的交线上，因为平面A1D1DA∩平面BCDA＝AD，所以M∈AD成立．所以点D，A，M三点共线．1．证明三点共线的方法(1)首先找出两个平面，然后证明这三点都是这两个平面的公共点，根据基本事实3可知，这些点都在两个平面的交线上；(2)选择其中两点确定一条直线，然后证明另一点也在此直线上．2．证明三线共点的步骤(1)首先说明两条直线共面且交于一点；(2)说明这个点在另两个平面上，并且这两个平面相交；(3)得到交线也过此点，从而得到三线共点．　　　　 [跟踪训练]1．如图所示，在空间四边形各边AD，AB，BC，CD上分别取E，F，G，H四点，如果EF，GH交于一点P，求证：点P在直线BD上．证明：若EF，GH交于一点P，则E，F，G，H四点共面，又因为EF⊂平面ABD，GH⊂平面CBD，所以P∈平面ABD，且P∈平面CBD，又因为平面ABD∩平面CBD＝BD，由基本事实3可得P∈BD.2.已知△ABC在平面α外，AB∩α＝P，AC∩α＝R，BC∩α＝Q，如图．求证：P，Q，R三点共线．证明：法一：∵AB∩α＝P，∴P∈AB，P∈平面α.又AB⊂平面ABC，∴P∈平面ABC.∴由基本事实3可知：点P在平面ABC与平面α的交线上，同理可证Q，R也在平面ABC与平面α的交线上．∴P，Q，R三点共线．法二：∵AP∩AR＝A，∴直线AP与直线AR确定平面APR.又∵AB∩α＝P，AC∩α＝R，∴平面APR∩平面α＝PR.∵B∈平面APR，C∈平面APR，∴BC⊂平面APR.又∵Q∈平面APR，Q∈α，∴Q∈PR.∴P，Q，R三点共线.平面的交线问题[例4]　如图所示正方体ABCD­A1B1C1D1中，E是棱CC1上一点．试说明D1，A，E 3点确定的平面与平面ABCD相交，并画出这两个平面的交线．[解]　因为A∈面D1AE，A∈面ABCD，所以面D1AE∩面ABCD≠∅，即面D1AE与面ABCD相交．延长D1E与DC，设它们相交于F，连接AF，如图所示，则F∈直线D1E，直线D1E⊂面D1AE，F∈直线DC，直线DC⊂面ABCD，则F∈面D1AE∩面ABCD，从而AF即为面D1AE与面ABCD的交线．找两个平面交线的突破口基本事实3告诉我们，如果两个平面有一个公共点，那么它们必定还有其他公共点，只要找出这两个平面的两个公共点，就找到了它们的交线．因此找两个平面的交线的突破口就是找这两个平面的两个公共点．　　　　 [跟踪训练]如图，E，F分别是正方体ABCD­A1B1C1D1的棱CC1，AA1的中点，试画出平面BED1F与平面ABCD的交线．解：如图，在平面AA1D1D内，D1F与DA不平行，分别延长D1F与DA，则D1F与DA必相交，设交点为M.因为M∈D1F，M∈DA，D1F⊂平面BED1F，DA⊂平面ABCD，所以M∈平面BED1F∩平面ABCD，又B∈平面BED1F∩平面ABCD，连接MB，则平面BED1F∩平面ABCD＝MB.故直线MB即为所求两平面的交线．1．经过空间任意三点作平面(　　)A．只有一个　　　　　　 B．可作两个C．可作无数多个  D．只有一个或有无数多个解析：选D　当三点在一条直线上时，过这三点能作无数个平面；当三点不在同一条直线上时，过这三点的平面有且只有一个．故选D.2．如果A点在直线a上，而直线a在平面α内，点B在α内，可以表示为(　　)A．A⊂a，a⊂α，B∈α  B．A∈a，a⊂α，B∈αC．A⊂a，a∈α，B⊂α  D．A∈a，a∈α，B∈α解析：选B　A点在直线a上，而直线a在平面α内，点B在α内，表示为A∈a，a⊂α，B∈α.3．若平面α与平面β相交，点A，B既在平面α内又在平面β内，则点A，B必在________．解析：设α∩β＝l，因为A，B∈α且A，B∈β，所以A，B∈l.答案：α与β的交线上4．不重合的三条直线，若相交于一点，最多能确定________个平面．解析：三条直线相交于一点，最多可确定3个平面，如图所示，直线a，b，c相交于点A，直线a，b确定平面α，直线b，c确定平面β，直线a，c确定平面γ，共3个平面．答案：35．若α∩β＝l，A，B∈α，C∈β，试画出平面ABC与平面α，β的交线．解：∵若α∩β＝l，A，B∈α，∴AB是平面ABC与α的交线，延长BA交l于D，则D∈平面ABC，∵C∈β，∴CD是平面ABC与β的交线，则对应的图示如图．