高中北师大版 (2019)6.1 探究w对y=sinwx的图象的影响综合训练题

1.6　函数y=Asin(ωx+φ)的性质与图象

1.6.1　探究ω对y=sin ωx的图象的影响

1.6.2　探究φ对y=sin(x+φ)的图象的影响

 1.6.3　探究A对y=Asin(ωx+φ)的图象的影响

1.函数y=2sin+1的最大值是(　　)

A.1 B.2 C.3 D.4

【解析】函数y=2sin+1的最大值为2+1=3.

【答案】C

2.已知函数f(x)=sin(ω>0)的最小正周期为π，则f=(　　)

A.- B. C. D.-

【解析】由=π，得ω=2，此时f(x)=sin.

所以f=sin.

【答案】B

3.函数y=3sin的一个单调递减区间为(　　)

A. B.

C. D.

【解析】y=3sin=-3sin，当x∈时，x-，此时y=sin在区间上单调递增，而y=-3sin在区间上单调递减，即单调递减区间是.

【答案】B

4.已知简谐运动f(x)=2sinx+φ|φ|<的图象经过点(0，1)，则该简谐运动的最小正周期T和初相φ分别为(　　)

A.T=6，φ= B.T=6，φ=

C.T=6π，φ= D.T=6π，φ=

【解析】T==6，

因为图象过(0，1)点，所以sin φ=.

因为-<φ<，所以φ=.

【答案】A

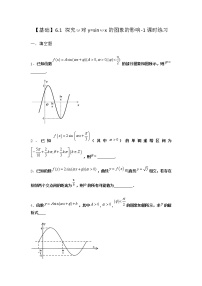
5.下列函数中，图象的一部分如图所示的是(　　)

A.y=sinx+ B.y=sin2x-

C.y=cos4x- D.y=cos2x-

【解析】设y=Asin(ωx+φ)，显然A=1，

又图象过点-，0，，1，

所以解得ω=2，φ=.

所以函数解析式为y=sin2x+=cos2x-.

【答案】D

6.已知ω>0，0<φ<π，直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴，则φ=(　　)

A. B. C. D.

【解析】由题意可知，函数f(x)的周期T=2×=2π，故ω=1，所以f(x)=sin(x+φ).令x+φ=kπ+(k∈Z)，将x=代入可得φ=kπ+(k∈Z).因为0<φ<π，所以φ=.

【答案】A

7.(多选)关于函数f(x)=4sin2x+(x∈R)的说法正确的是(　　)

A.y=f(x)的解析式可改写为y=4cos2x-

B.y=f(x)是以2π为最小正周期的周期函数

C.y=f(x)的图象关于点-，0对称

D.y=f(x)的图象关于直线x=-对称

【解析】4sin2x+=4cos-2x=4cos2x-，A正确;f(x)的最小正周期为T==π，B不正确;而C中f-=0，-，0是对称中心，故C正确;f(x)的对称直线满足2x++kπ，即x=，k∈Z，将x=-代入，k=∉Z，D不正确.

【答案】AC

8.函数y=6sin的振幅是　　　　，周期是　　　　，频率是　　　　，初相是　　　　，图象最高点的坐标是　　　　. 

【解析】由题意，得A=6，T==8π，，φ=-.

当=2kπ+(k∈Z)，

即x=8kπ+(k∈Z)时，函数取得最大值6.

【答案】6　8π　　-　8kπ+，6(k∈Z)

9.将函数y=sin的图象上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y=g(x)的图象，则函数g(x)在上的最大值和最小值分别为　　　和　　　. 

【解析】依据图象变换得函数g(x)=sin.

因为x∈，所以4x+，

所以当4x+时，g(x)取最大值;当4x+时，g(x)取最小值-.

【答案】　-

10.设函数f(x)=sin(2x+φ)(-π<φ<0)，y=f(x)图象的一条对称轴是直线x=.

(1)求φ;

(2)求函数y=f(x)的单调区间及最值.

解(1)y=f(x)图象的一条对称轴是直线x=，

则有sin+φ=±1，即+φ=kπ+(k∈Z)，

所以φ=kπ+(k∈Z)，又-π<φ<0，则φ=-.

(2)令2kπ-≤2x-≤2kπ+(k∈Z)，

则kπ+≤x≤kπ+(k∈Z)，

即函数y=f(x)的单调递增区间为kπ+，kπ+(k∈Z).

再令2kπ+≤2x-≤2kπ+(k∈Z)，

则kπ+≤x≤kπ+(k∈Z)，

即函数y=f(x)的单调递减区间为

kπ+，kπ+(k∈Z).

当2x-=2kπ+，即x=kπ+(k∈Z)时，

函数取得最大值1;

当2x-=2kπ-，即x=kπ+(k∈Z)时，

函数取得最小值-1.

1.(多选)已知函数y=，以下说法正确的是(　　)

A.周期为

B.偶函数

C.函数图象的一条对称轴为直线x=

D.函数在区间上单调递减

【解析】根据函数图象(图略)可知，函数的周期T=;因为f(-x)=sin-2x-=sin2x+，所以该函数既不是奇函数，也不是偶函数;令2x-，即x=，k∈Z，当k=0时，x=，故函数的一条对称轴为直线x=;函数y=sin2x-在区间上单调递减，但y=sin2x-在区间上单调递增.

【答案】AC

2.(多选)(2020济南高二期中)函数f(x)=2sin(2x+φ)0<φ<，且f(0)=1，则下列结论中不正确的是 (　　)

A.f(φ)=2

B.，0是f(x)图象的一个对称中心

C.φ=

D.x=-是f(x)图象的一条对称轴

【解析】由f(0)=1，且0<φ<，可得φ=，选项C错误;可得f(x)=2sin2x+，把x=代入f(x)=2sin2x+，得f(φ)=2，选项A正确;f=2，f(x)取得最大值，选项B错误;而f-=-1，非最值，选项D错误.

【答案】BCD

3.将函数f(x)=3sin图象上所有点的横坐标伸长到原来的2倍，再向右平移个单位长度，得到函数y=g(x)的图象，则y=g(x)图象的一条对称轴是(　　)

A.x= B.x=

C.x= D.x=

【解析】将函数f(x)=3sin图象上所有点的横坐标伸长到原来的2倍，可得函数y=3sin的图象，再向右平移个单位长度，可得y=3sin2x-+=3sin的图象，故g(x)=3sin.

令2x-=kπ+，k∈Z，得到x=，k∈Z，则得y=g(x)图象的一条对称轴是x=.故选C.

【答案】C

4.要得到y=sin的图象，需将函数y=cos的图象上所有的点至少向左平移　　　　个单位长度. 

【解析】cos=sin，将y=sin的图象上所有的点向左平移φ(φ>0)个单位长度得y=sin的图象.令=2kπ+，所以φ=4kπ-，k∈Z.所以当k=1时，φ=是φ的最小正值.

【答案】

5.函数f(x)=Asin+1(A>0，ω>0)的最大值为3，其图象相邻两条对称轴之间的距离为.

(1)求函数f(x)的解析式;

(2)设α∈(0，2π)，f=2，求α的值.

解(1)因为函数f(x)的最大值为3，所以A+1=3，即A=2.

因为函数图象相邻两条对称轴之间的距离为，

所以最小正周期T=π，所以ω=2.所以函数f(x)的解析式为f(x)=2sin2x-+1.

(2)f=2sin+1=2，即sin.

因为0<α<2π，所以-<α-，

所以α-或α-，故α=或α=π.

6.已知函数f(x)=2sinωx+φ-+1(0<φ<π，ω>0)为偶函数，且函数f(x)的图象的两相邻对称轴间的距离为.

(1)求f的值;

(2)将函数f(x)的图象向右平移个单位长度后，再将得到的图象上各点的横坐标伸长为原来的4倍，纵坐标不变，得到函数g(x)的图象，求函数g(x)的单调递减区间.

解(1)因为f(x)为偶函数，所以φ-=kπ+(k∈Z)，

所以φ=kπ+(k∈Z).

又0<φ<π，所以φ=，

所以f(x)=2sinωx++1=2cos ωx+1.

又函数f(x)的图象的两相邻对称轴间的距离为，

所以T==2×，所以ω=2，

所以f(x)=2cos 2x+1，

所以f=2cos2×+1=+1.

(2)将f(x)的图象向右平移个单位长度后，

得到函数fx-的图象，

再将所得图象上各点的横坐标伸长为原来的4倍，

纵坐标不变，得到f的图象，

所以g(x)=f=2cos2+1=2cos+1.

当2kπ≤≤2kπ+π(k∈Z)，即4kπ+≤x≤4kπ+(k∈Z)时，g(x)单调递减.所以函数g(x)的单调递减区间是4kπ+，4kπ+(k∈Z).