浙江省金华市义乌市八年级上学期期末含解析练习题

 八年级上学期期末数学试卷

一、单选题

1．点P（−5，3）在（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

2．如图，己知图形X和直线l，以直线l为对称轴，图形X的轴对称图形是(　　)

A． B．

C． D．

3．一个不等式的解集在数轴上表示如图所示，则这个不等式可能是（　　）

A． B． C． D．

4．如图给出的三角形有一部分被遮挡，则这个三角形可能是（　　）

A．直角三角形 B．锐角三角形 C．钝角三角形 D．等边三角形

5．是不等式的一个解，则的值不可能是（　　）

A．1 B．2 C．3 D．4

6．下列叙述有误的是（　　）

A．三角形任何两边的和大于第三边

B．对称轴一定垂直平分连结两个对称点的线段

C．所有的等边三角形都是全等图形

D．物体在平面上的位置可以用第几行第几列来确定，也可以用方向和距离来确定

7．在正比例函数y＝kx中，y的值随着x值的增大而减小，则一次函数y＝kx+k在平面直角坐标系中的图象大致是（　　） 

A． B．

C． D．

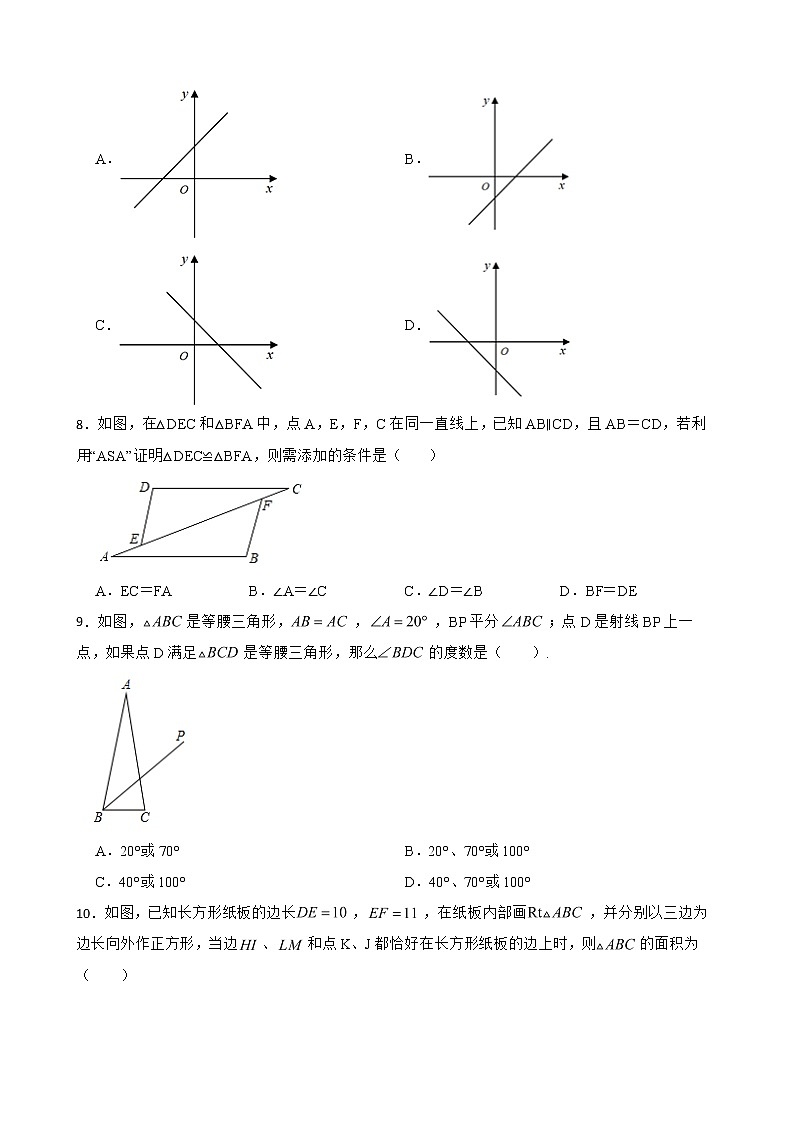
8．如图，在△DEC和△BFA中，点A，E，F，C在同一直线上，已知AB∥CD，且AB＝CD，若利用“ASA”证明△DEC≌△BFA，则需添加的条件是（　　）

A．EC＝FA B．∠A＝∠C C．∠D＝∠B D．BF＝DE

9．如图，是等腰三角形，，，BP平分；点D是射线BP上一点，如果点D满足是等腰三角形，那么的度数是（　　）.

A．20°或70° B．20°、70°或100°

C．40°或100° D．40°、70°或100°

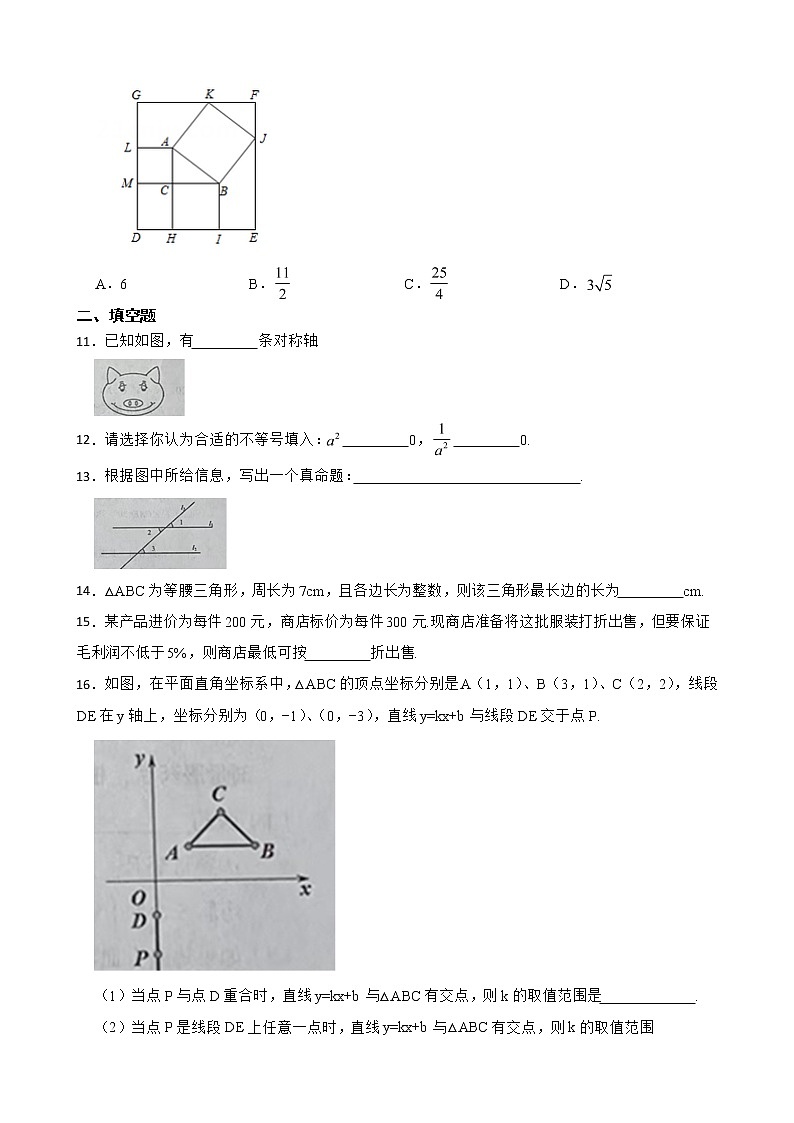
10．如图，已知长方形纸板的边长，，在纸板内部画，并分别以三边为边长向外作正方形，当边、和点K、J都恰好在长方形纸板的边上时，则的面积为（　　）

A．6 B． C． D．

二、填空题

11．已知如图，有　     　条对称轴.

12．请选择你认为合适的不等号填入：　     　0，　     　0.

13．根据图中所给信息，写出一个真命题：　                           　.

14．△ABC为等腰三角形，周长为7cm，且各边长为整数，则该三角形最长边的长为　     　cm.

15．某产品进价为每件200元，商店标价为每件300元.现商店准备将这批服装打折出售，但要保证毛利润不低于5%，则商店最低可按　     　折出售.

16．如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（1，1）、B（3，1）、C（2，2），线段DE在y轴上，坐标分别为（0，−1）、（0，−3），直线y=kx+b与线段DE交于点P.

（1）当点P与点D重合时，直线y=kx+b与△ABC有交点，则k的取值范围是　         　.

（2）当点P是线段DE上任意一点时，直线y=kx+b与△ABC有交点，则k的取值范围是　         　.

三、解答题

17．解不等式组.

18．如图，在每个小正方形的边长为1个单位的网格中建立平面直角坐标系，已知线段的两个端点均在格点（网格线的交点）上，且，.

（1）将线段向上平移2个单位，再向右平移5个单位得到线段，画出线段（点，分别为A，B的对应点）；

（2）若点为线段上任意一点，经过（1）的平移后，在线段上对应的点的坐标为　               　.

19．如图，已知一次函数，与x轴的交点横坐标分别为6和，、的交点P（3，n）.

（1）求、的函数解析式；

（2）x取何值时，函数的图象在函数图象的上方？

20．如图，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且BE=BF.

（1）求证：△ABE≌△CBF；

（2）若∠CAE=30°，求∠ACF的度数.

21．某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，那么当成人按规定量服药后，根据图象回答下列问题：

（1）服药　     　小时，血液中含药量最高，达到每毫升　     　微克，接着逐步衰减.服药后5小时，血液中含药量每毫升　     　微克.

（2）如果每毫升血液中含药量为3微克及以上时治疗疾病有效.某老师要在上午8：00~11：30之间参加活动，则该老师在哪个时间段内服药，才能使药效持续有效？请你通过计算说明.

22．12月，浙江突发疫情，我市立即启动疫情应急处置模拟演练.为配合演练顺利开展，某校需要购进A、B两款体温枪共100只.已知购进A型体温枪花费1000元，B型体温枪花费1500元，A型体温枪的价格比B型高50元，B型体温枪的数量是A型的两倍.

（1）求每只A型、B型体温枪的价格；

（2）若购进B型体温枪的数量不超过A型体温枪的2倍，设购进A型体温枪x只，这100只体温枪的总费用为y元.

①求y关于x的函数关系式；

②某校实际购买时，发现某店对A型体温枪进行降价处理，比原价降低a元出售（，且a为正整数），且限定一次性最多购买A型体温枪50只，当a满足什么条件时，能使该校购进这100只体温枪总费用最小.

23．如图，长方形，点E是上的一点，将沿折叠后得到，且点O在长方形内部.已知，.

（1）如图1，若，求四边形的面积.

（2）如图2，延长交于F，连结，将沿折叠，当点D的对称点恰好为点O时，求四边形的面积.

（3）如图3，在（2）的条件下，延长交于点G，连结，将沿折叠，当点C的对称点恰好为点O时，求四边形的面积.

24．如图，已知为等腰直角三角形，且面积为4.点D是的中点，点F是直线上一动点，连结.

（1）求线段的长；

（2）当点E在射线上，且时，连结，若，试判断是否为等腰三角形，并说明理由；

（3）直线上是否存在点F（F不与重合），使的其中两边之比为？若存在，求出的长；若不存在，请说明理由.

答案解析部分

【解析】【解答】解：∵点P的坐标为（-5，3），

∴点P的横坐标为负数，纵坐标为正数，

∴点P在第二象限.

故答案为：B.

【分析】若A（m，n），当m>0，n>0时，点A在第一象限；当m<0，n>0时，点A在第二象限；当m<0，n<0时，点A在第三象限；当m>0，n<0时，点A在第四象限，据此判断即可得出答案.

【解析】【解答】解：以直线l为对称轴，图形X的轴对称图形是选项C中的图形.
故答案为：C.
【分析】轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合，观察各选项中的图形可得答案.

【解析】【解答】解：∵−1处是空心圆点，且折线向右，

∴这个不等式的解集是x＞−1.

故答案为：A.

【分析】根据数轴上表示不等式解集的方法：大向右，小向左，实心等于，空心不等，即可得出答案.

【解析】【解答】解：由图形可得：该三角形为锐角三角形.

故答案为：B.

【分析】观察图形可知：图中的三角形有两个锐角，且第三个角也小于90°，据此可判断出三角形的形状.

【解析】【解答】解：∵

是不等式的一个解，

∴

故答案为：A.

【分析】根据x=1为不等式的解集可得b>1，据此判断.

【解析】【解答】解：A、三角形任何两边的和大于第三边，正确；

B、对称轴一定垂直平分连结两个对称点的线段，正确；

C、所有的等边三角形不一定全等，选项错误；

D、物体在平面上的位置可以用第几行第几列来确定，也可以用方向和距离来确定，正确.

故答案为：C.

【分析】根据三角形的三边关系可判断A；根据轴对称图形的概念可判断B；根据全等图形的概念可判断C；根据坐标确定位置的方法可判断D.

【解析】【解答】解：∵正比例函数y＝kx中，y的值随着x值的增大而减小，

∴k＜0，

∴一次函数y＝kx+k与y轴的交点在y轴的负半轴，

∴一次函数y＝kx+k的图像经过第二、三、四象限，

故答案为：D．

【分析】根据正比例的性质与系数的关系可得k<0，再利用一次函数的图象与系数的关系可得答案。

【解析】【解答】解：需添加的条件是∠D=∠B，

理由是：∵AB∥CD，

∴∠A=∠C，

在△DEC和△BFA中，

，

∴△DEC≌△BFA（ASA）.

故答案为：C.

【分析】根据平行线的性质可得∠A=∠C，由已知条件可知AB=CD，然后找出与AB、CD相邻的另一组角即可.

【解析】【解答】解：当时，如图所示，

，，

，

平分，

，

，

，

当时，如图所示，

，，

，

平分，

，

，

.

当时，如图所示，

，，

，

平分，

，

，

，

故的度数是：、或.

故答案为：D.

【分析】当BC=CD时，根据等腰三角形的性质以及内角和定理可得∠ABC=80°，根据角平分线的概念可得∠CBD=40°，然后根据等腰三角形的性质可得∠BDC的度数；当BD=BC时，同理可得∠ABC=80°，∠CBD=40°，然后根据等腰三角形的性质以及内角和定理可得∠BDC的度数；当DB=DC时，同理可得∠CBD=40°，然后根据等腰三角形的性质以及内角和定理可得∠BDC的度数.

【解析】【解答】解：延长CA与GF交于点N，延长CB与EF交于点P，

设AC=b，BC=a，则AB=，

∵四边形ABJK是正方形，四边形ACML是正方形，四边形BCHI是正方形，

∴AB=BJ，∠ABJ=90°，

∴∠ABC+∠PBJ=90°=∠ABC+∠BAC，

∴∠BAC=∠JBP，

∵∠ACB=∠BPJ=90°，

∴△ABC≌△BJK（AAS），

同理△ABC≌△BJK≌△JKF≌△KAN，

∴AC=BP=JF=KN=NG=b，BC=PJ=FK=AN=PE=a，

∵DE=10，EF=11，

∴2b+a=10，2a+b=11，

∴a+b=7，

∴a2+b2=49-2ab，

∵长方形DEFG的面积=十个小图形的面积和，

∴10×11=3ab+ab×4+a2+b2+（）2，

整理得：5ab+2（a2+b2）=110，

把a2+b2=49-2ab，代入得：5ab+2（49-2ab）=110，

∴ab=12，

∴△ABC的面积为ab=6.

故答案为：A.

【分析】延长CA交GF于N，延长CB交EF交于P，设AC=b，BC=a，则AB=，由正方形性质得AB=BJ，∠ABJ=90°，根据同角的余角相等得∠BAC=∠JBP，利用AAS证明△ABC≌△BJK，同理可证△ABC≌△BJK≌△JKF≌△KAN，根据全等三角形的对应边相等及正方形的性质得AC=BP=JF=KN=NG=b，BC=PJ=FK=AN=PE=a，根据DE=10，EF=11可得a+b=7，结合完全平方公式可得a2+b2=49-2ab，根据图形可知：长方形DEFG的面积=十个小图形的面积和，据此可得5ab+2(a2+b2)=110，联立可得ab的值，进而可得△ABC的面积.

【解析】【解答】解：由题可知，共有条对称轴.

故答案为：1.

【分析】观察图形可知：沿着中间的竖直线折叠可使原图形的左右两边重合，据此可得对称轴的条数.

【解析】【解答】解：a20；；

故答案为：，.

【分析】根据偶次幂的非负性以及分式的分母不能为0进行解答.

【解析】【解答】解：如果，那么 （答案不唯一）

故答案为：如果，那么.

【分析】根据平行线的判定定理写出一个真命题即可.

【解析】【解答】解：设腰长为x，则底边为7-2x.

∵7-2x-x＜x＜7-2x+x，

∴1.75＜x＜3.5，

∵三边长均为整数，

∴x可取的值为2或3，

故各边的长为2，2，3或3，3，1.

∴该三角形最长边的长为3cm.

故答案为：3.

【分析】设腰长为x，则底边为7-2x，根据三角形的三边关系可得x的范围，结合x为整数可得x的值，进而得到三角形的三边长，据此可得最长边的长.

【解析】【解答】解：设售价可以按标价打x折，

根据题意，得：200+200×5%≤300×，

解得：x≥7，

答：售价最低可按标价的7折.

故答案为：7.

【分析】设售价可以按标价打x折，由题意可得售价为300×元，利润为200×5%元，根据进价+利润可得售价，据此列出不等式，求解即可.

【解析】【解答】解：（1）当直线y=kx+b经过A（1，1），D（0，−1）时，

，解得，

当直线y=kx+b经过B（3，1），D（0，−1）时，

，解得，

当直线y=kx+b经过C（2，2），D（0，−1）时，

，解得，

所以直线y=kx+b与△ABC有交点，则k的取值范围是：；

（2）当直线y=kx+b经过A（1，1）时，

k+b=1，即b=1-k，

∵点P是线段DE上任意一点，且D （0，−1）、E （0，−3），即，

∴，

解得：，

当直线y=kx+b经过B（3，1）时，

3k+b=1，即b=1-3k，

∵点P是线段DE上任意一点，且D （0，−1）、E （0，−3），即，

∴，

解得：，

∴直线y=kx+b与△ABC有交点，则k的取值范围是.

故答案为：（1）；（2）.

【分析】（1）分别求出直线y=kx+b经过A（1，1），D（0，−1）或B（3，1），D（0，−1）或C（2，2），D（0，−1）时对应的k、b的值，进而可得k的范围；

（2）将A（1，1）代入y=kx+b中可得b=1-k，根据点P为线段DE上的点可得k的范围；同理求出直线过点B时k的范围，据此不难求出满足题意的k的范围.

【解析】【分析】首先分别求出两个不等式的解集，然后根据口诀：同大取大，同小取小，大小小大中间找，大大小小无解了，取其公共部分即为不等式组的解集.

【解析】【解答】解：（2）在线段A′B′上对应的点P′的坐标为（m＋5，n＋2）.

故答案为：（m＋5，n＋2）.

【分析】（1）分别将点A、B向上平移2个单位，再向右平移5个单位得到点A′、B′，连接可得线段A′B′；
（2）将点P（m，n）先向上平移2个单位，再向右平移5个单位就可得到点P′的坐标.

【解析】【分析】（1）易得直线l2与x轴的交点为（-1，0），代入y=x+a中求出a的值，据此可得直线l2的解析式；将P（3，n）代入l2解析式中求出n的值，可得点P的坐标，将P点的坐标以及（6，0）代入y=kx+b中求出k、b，进而可得直线l1的解析式；
（2）联立两一次函数解析式求出x、y，可得交点坐标，然后找出y=kx+b的图象在y=x+5上方部分所对应的x的范围即可.

【解析】【分析】（1）易得∠CBF=∠ABE=90°，由已知条件可知AB=BC，BE=BF，然后根据全等三角形的判定定理SAS进行证明；
（2）易得∠CAB=∠ACB=45°，则∠BAE=∠CAB-∠CAE=15°，根据全等三角形的性质可得∠BCF=∠BAE=15°，然后根据∠ACF=∠BCF+∠ACB进行计算.

【解析】【解答】（1）解：设直线AB的解析式为y=kx+b，由题意，得

，解得：，

∴y=-x+8（2<x8），

当x=5时，y=3，

由函数图象，得

服药后2小时，血液中含药量最高为每毫升6微克.服药后5小时，血液中含药量每毫升3微克

故答案为：2，6，3；

【分析】（1）设直线AB的解析式为y=kx+b，将（2，6）、（8，0）代入求出k、b的值，据此可得函数解析式，令x=5，求出y的值，据此解答；
（2）当x≤2时，设y与x之间的函数关系式y=k1x，将（2，6）代入求出k1的值，据此可得函数解析式，令y=3，求出x的值，据此解答.

【解析】【分析】（1）设每只A型温枪的价格为m元，则每只B型温枪的价格为（m-50）元，由题意可得1000元可购买A型体温枪的数量为只，1500元可购买B型体温枪的数量为只，然后根据B型体温枪的数量是A型的两倍建立方程，求解即可；
（2）①设购进A型体温枪x只，则购进B型体温枪（100-x）只，根据数量×单价可得y与x的关系式，根据“购进B型体温枪的数量不超过A型体温枪的2倍”列出不等式，求出x的范围，据此解答；
②根据数量×单价可得y与x的关系式，然后根据一次函数的性质进行解答.

【解析】【分析】（1）根据长方形的性质得∠A=∠D=∠C=90°，CD=AB=4，AD=BC=，根据折叠的性质可得△OBE≌△ABE，根据含30°角的直角三角形的性质可得AE=BE，利用勾股定理可得AB，然后求出AE，接下来根据S四边形ABOE=S△ABE+S△OBE=2S△ABE进行计算；
（2）根据全等三角形的性质可得OE=AE， OB=AB=4，根据折叠的性质可得△OEF≌△DEF，则OE =DE，OF=DF，推出OE=AE=DE=AD=，设OF=DF=x，则FC=4-x，BF=4＋x，利用勾股定理求出x，然后根据S四边形ABFE=S△ABE+S△BEF进行计算；
（3）根据全等三角形的性质可得OF=DF，根据折叠的性质可得△CGF≌△OGF，得到OF=FC， ∠FOG=90°，则DF=FC=DC=2，设OG=a，则CG=a，在Rt△BOG中，由勾股定理可得a的值，然后根据S四边形BEFG=S△BEF+S△BFG进行计算.

【解析】【分析】（1）根据等腰直角三角形的性质以及三角形的面积公式可得AB=AC=2，然后利用勾股定理求解即可；
（2）过点F作FH⊥BE于点H，根据等腰直角三角形的性质可得∠ABC=∠BCA=45°，根据已知条件求出BF，利用勾股定理可得BH，根据中点的概念可得BD=DC=2，则DH=BH-BD=6，然后在Rt△DHF中，应用勾股定理求出DF，然后求出DE，据此判断；
（3）根据等腰直角三角形的性质可得∠BAC=∠FAC=90°，①当AC∶CF=1∶时，易得CF、AF的值，然后根据BF=AB+ AF进行计算；②当AC∶AF=1∶时，同理可得BF的值；③当AF∶AC=1∶时，同理可得BF.