

浙教版数学复习阶梯训练:二次函数含解析(优生集训)4
展开
这是一份浙教版数学复习阶梯训练:二次函数含解析(优生集训)4,共22页。试卷主要包含了综合题等内容,欢迎下载使用。
二次函数 (优生集训)
一、综合题
1.九(4)班数学兴趣小组经过市场调查,整理出童威的某种高端商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销售(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在前49天销售中,每销售一件商品就捐赠m元(0<m<10)给希望工程.若前49天销售获得的最大日利润为5408元,则m= .
2.如图1,已知抛物线y=ax2经过点(﹣2,1).
(1)求抛物线的解析式;
(2)若直线y= x+2交抛物线于点C、D,点P是直线CD下方的抛物线上一动点,若S△PCD最大,求此时点P的坐标,并求出S△PCD的最大值;
(3)如图2,直线y=kx+2与抛物线交于点E,F,点P是抛物线上的动点,延长PE,PF分别交直线y=﹣2于M,N两点,MN交y轴于Q点,求QM•QN的值.
3.已知抛物线与x轴交于点A、点B,与y轴交于点C(0,3),顶点坐标(﹣2,﹣1).
(1)求抛物线的解析式.
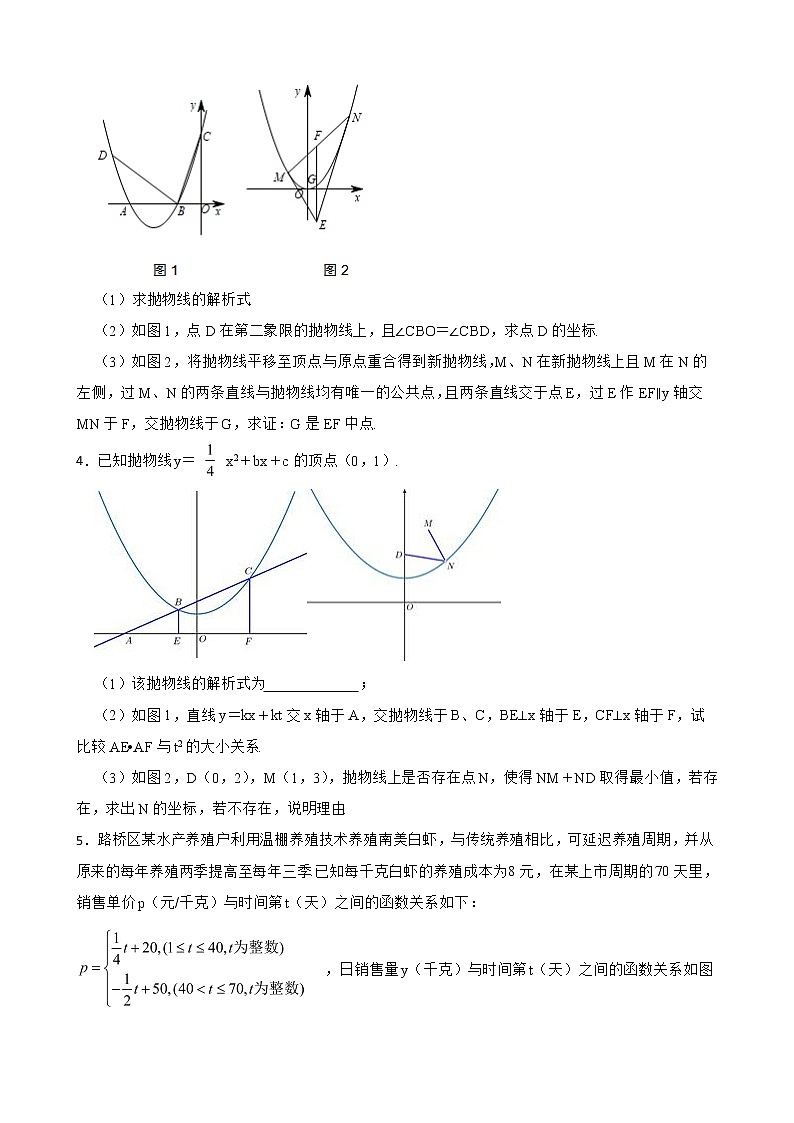
(2)如图1,点D在第二象限的抛物线上,且∠CBO=∠CBD,求点D的坐标.
(3)如图2,将抛物线平移至顶点与原点重合得到新抛物线,M、N在新抛物线上且M在N的左侧,过M、N的两条直线与抛物线均有唯一的公共点,且两条直线交于点E,过E作EF∥y轴交MN于F,交抛物线于G,求证:G是EF中点.
4.已知抛物线y= x2+bx+c的顶点(0,1).
(1)该抛物线的解析式为 ;
(2)如图1,直线y=kx+kt交x轴于A,交抛物线于B、C,BE⊥x轴于E,CF⊥x轴于F,试比较AE•AF与t2的大小关系.
(3)如图2,D(0,2),M(1,3),抛物线上是否存在点N,使得NM+ND取得最小值,若存在,求出N的坐标,若不存在,说明理由.
5.路桥区某水产养殖户利用温棚养殖技术养殖南美白虾,与传统养殖相比,可延迟养殖周期,并从原来的每年养殖两季提高至每年三季.已知每千克白虾的养殖成本为8元,在某上市周期的70天里,销售单价p(元/千克)与时间第t(天)之间的函数关系如下: ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量y与时间t的函数关系式;
(2)求第几天的日销售利润最大?最大利润是多少元?
(3)在实际销售的前40天中,该养殖户决定每销售1千克白虾,就捐赠 元给公益事业.在这前40天中,已知每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
6.在平面直角坐标系中,已知抛物线C:y=ax2+2x﹣1(a≠0)和直线l:y=kx+b,点A(﹣3,﹣3),B(1,﹣1)均在直线l上.
(1)求出直线l的解析式;
(2)当a=﹣1,二次函数y=ax2+2x﹣1的自变量x满足m≤x≤m+2时,函数y的最大值为﹣4,求m的值;
(3)若抛物线C与线段AB有两个不同的交点,求a的取值范围.
7.如图,抛物线 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且 .
(1)求抛物线的函数关系式;
(2)若P是抛物线上且位于直线 上方的一动点,求 的面积的最大值及此时点P的坐标;
(3)在线段 上是否存在一点M,使 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
8.如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
(1)n=3m-9(用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值;
(3)①设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
9.如图,抛物线 与 轴交于 、 两点,与 轴交于点 .直线 与抛物线交于 、 两点,与 轴交于点 ,点 的坐标为 .
(1)求抛物线的解析式与直线 的解析式;
(2)若点 是抛物线上的点且在直线 上方,连接 、 ,求当 面积最大时点 的坐标及该面积的最大值;
(3)若点 是 轴上的点,且 ,求点 的坐标.
10.科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
(1)直接写出与之间的函数关系式;
(2)求出与之间的函数关系式;
(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
11.如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(﹣1,0),B(0,3),顶点为C.平移此抛物线,得到一条新的抛物线,且新抛物线上的点D(3,﹣1)为原抛物线上点A的对应点,新抛物线顶点为E,它与y轴交于点G,连接CG,EG,CE.
(1)求原抛物线对应的函数表达式;
(2)在原抛物线或新抛物线上找一点F,使以点C,E,F,G为顶点的四边形是平行四边形,并求出点F的坐标;
(3)若点K是y轴上的一个动点,且在点B的上方,过点K作CE的平行线,分别交两条抛物线于点M,N,且点M,N分别在y轴的两侧,当MN=CE时,请直接写出点K的坐标.
12.已知O为坐标原点,直线l:y=﹣ x+2与x轴、y轴分别交于A、C两点,点B(4,2)关于直线l的对称点是点E,连接EC交x轴于点D.
(1)求证:AD=CD;
(2)求经过B、C、D三点的抛物线的函数表达式;
(3)当x>0时,抛物线上是否存在点P,使S△PBC= S△OAE?若存在,求点P的坐标;若不存在,说明理由.
13.某品牌汽车销售店销售某种品牌的汽车,每辆汽车的进价16(万元).当每辆售价为22(万元)时,每月可销售4辆汽车.根据市场行情,现在决定进行降价销售.通过市场调查得到了每辆降价的费用 (万元)与月销售量 (辆)( )满足某种函数关系的五组对应数据如下表:
4
5
6
7
8
0
0.5
1
1.5
2
(1)请你根据所给材料和初中所学的函数知识写出 与 的关系式 ;
(2)每辆原售价为22万元,不考虑其它成本,降价后每月销售利润y=(每辆原售价- -进价)x,请你根据上述条件,求出月销售量 为多少时,销售利润最大?最大利润是多少?
14.如图,直线 与x轴交于点B,与y轴交于点A,点P为线段 的中点,点Q是线段 上一动点(不与点O、A重合).
(1)请直接写出点A、点B、点P的坐标;
(2)连接 ,在第一象限内将 沿 翻折得到 ,点O的对应点为点E.若 ,求线段 的长;
(3)在(2)的条件下,设抛物线 的顶点为点C.
①若点C在 内部(不包括边),求a的取值范围;
②在平面直角坐标系内是否存在点C,使 最大?若存在,请直接写出点C的坐标;若不存在,请说明理由.
15.如图,在平面直角坐标系 中,平行四边形 的 边与y轴交于E点,F是 的中点,B、C、D的坐标分别为 .
(1)求过B、E、C三点的抛物线的解析式;
(2)试判断抛物线的顶点是否在直线 上;
(3)设过F与 平行的直线交y轴于Q,M是线段 之间的动点,射线 与抛物线交于另一点P,当 的面积最大时,求P的坐标.
16.已知抛物线 与x轴交于点 和 ,与y轴交于点C,顶点为P,点N在抛物线对称轴上且位于x轴下方,连 交抛物线于M,连 、 .
(1)求抛物线的解析式;
(2)如图1,当 时,求M点的横坐标;
(3)如图2,过点P作x轴的平行线l,过M作 于D,若 ,求N点的坐标.
17.如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 .
(1)求抛物线的解析式;
(2) 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;
(3) 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.
18.已知二次函数 .
(1)若 , ,求方程 的根的判别式的值;
(2)如图所示,该二次函数的图象与 轴交于点 、 ,且 ,与 轴的负半轴交于点 ,点 在线段 上,连接 、 ,满足 , .
①求证: ;
②连接 ,过点 作 于点 ,点 在 轴的负半轴上,连接 ,且 ,求 的值.
19.抛物线 交 轴于 , 两点( 在 的左边).
(1) 的顶点 在 轴的正半轴上,顶点 在 轴右侧的抛物线上.
①如图(1),若点 的坐标是 ,点 的横坐标是 ,直接写出点 , 的坐标;
②如图(2),若点 在抛物线上,且 的面积是12,求点 的坐标;
(2)如图(3), 是原点 关于抛物线顶点的对称点,不平行 轴的直线 分别交线段 , (不含端点)于 , 两点,若直线 与抛物线只有一个公共点,求证 的值是定值.
20.红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件.一个月可售出5万件;月销售单价每涨价1元,月销售量就减少 万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
21.已知抛物线 与x轴相交于 , 两点,与y轴交于点C,点 是x轴上的动点.
(1)求抛物线的解析式;
(2)如图1,若 ,过点N作x轴的垂线交抛物线于点P,交直线 于点G.过点P作 于点D,当n为何值时, ;
(3)如图2,将直线 绕点B顺时针旋转,使它恰好经过线段 的中点,然后将它向上平移 个单位长度,得到直线 .
① ▲ ;
②当点N关于直线 的对称点 落在抛物线上时,求点N的坐标.
22.如图,已知抛物线 与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为 .
(1)求抛物线的解析式;
(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由.
(3)如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且 .在y轴上是否存在点F,使得 为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系 中,抛物线 与x轴相交于O,A两点,顶点P的坐标为 .点B为抛物线上一动点,连接 ,过点B的直线与抛物线交于另一点C.
(1)求抛物线的函数表达式;
(2)若点B的横坐标与纵坐标相等, ,且点C位于x轴上方,求点C的坐标;
(3)若点B的横坐标为t, ,请用含t的代数式表示点C的横坐标,并求出当 时,点C的横坐标的取值范围.
24.已知抛物线
(1)当 时,请判断点(2,4)是否在该抛物线上;
(2)该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;
(3)已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
25.如图,已知二次函数的图象与x轴交于A和B(-3,0)两点,与y轴交于C(0,-3),对称轴为直线 ,直线y=-2x+m经过点A,且与y轴交于点D,与抛物线交于点E,与对称轴交于点F.
(1)求抛物线的解析式和m的值;
(2)在y轴上是否存在点P,使得以D、E、P为顶点的三角形与△AOD相似,若存在,求出点P的坐标;若不存在,试说明理由;
(3)直线y=1上有M、N两点(M在N的左侧),且MN=2,若将线段MN在直线y=1上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号).
答案解析部分
【解析】【解答】解:(3)根据题意得, ,
函数的对称轴 ,
当 时,函数取得最大值,即 即 ,
解得: , (不合题意,舍去),
故m的值为6.
故答案为:6.
【分析】(1)根据利润=单价乘以销售量分段列出函数关系式可求解;
(2)根据分段函数的性质,可分别得出最大值,根据有理数大小的比较,可判断求解;
(3)在确定函数表达式的基础上,确定函数的对称轴可求解.
【解析】【分析】(1)将点(-2,1)代入y=ax2中求出a,据此可得抛物线的解析式;
(2)过点P作直线PE∥y轴交CD于E,设P(m,m2),则E(m,m+2),表示出PE,联立直线与抛物线解析式求出x、y,得到点C、D的坐标,然后根据三角形的面积公式以及面积间的和差关系表示出S△PCD,由二次函数的性质可得最大值以及对应的点P的坐标;
(3)设E(x1,x12),F(x2,x22),P(n,n2),表示出直线PE、PF的解析式,求出点M、N的横坐标,联立y=kx+2与抛物线的解析式得到关于x的一元二次方程,根据根与系数的关系可得x1+x2=4k,x1x2=-8,然后根据QM·QN=-xM·xN进行计算.
【解析】【分析】(1)由题意可设二次函数的解析式为y=a(x+2)2-1,将(0,3)代入可求出a,据此可得二次函数的解析式;
(2)过点C作CE∥x轴交直线BD与点E,由平行线的性质可得∠ECB=∠CBO,结合∠CBO=∠DBC可推出EB=EC,令二次函数解析式中的y=0,求出x,可得A(-3,0),B(-1,0),设E(m,3),表示出EC、EB,根据EB=EC可得m的值,进而得到点E的坐标,利用待定系数法求出直线BE的解析式,联立二次函数解析式求出x、y,据此可得点D的坐标;
(3)易得平移后的函数解析式为y=x2,设M(m,m2),N(n,n2),表示出直线ME、NE的解析式,分别联立直线ME、NE与二次函数的解析式,并结合根的判别式可得k1=2a,k2=2b,然后联立直线ME、NE的解析式可得x、y,得到点E的坐标,表示出直线MN的解析式,金额得到EF、GF,据此证明.
【解析】【解答】解:(1)将点(0,1)代入 中,得c=1,
由图象可知,抛物线 的对称轴为y轴,
所以 ,
解得b=0,
∴抛物线的解析式为: ,
故答案为: ;
【分析】(1)将点(0,1)代入y=x2+bx+c中可得c,根据函数的对称轴为y轴可得b的值,据此可得抛物线的解析式;
(2)设A的横坐标为x1,B的横坐标为x2,C的横坐标为x3,易得B、E的横坐标均为x2,C、F的横坐标均为x3,联立直线与抛物线解析式可得x2-4kx+4+4kt=0,由根与系数的关系可得x2+x3=4k,x2x3=4+4kt,令直线解析式中的y=0,求出x,即x1,然后表示出AE·AF,据此解答;
(3)过点N作NG⊥x轴,垂足为G,过点N作NJ⊥y轴,垂足为J,设N(a,a2+1),则J(a2+1,0),G(a,0),由勾股定理表示出ND,推出ND=NG,过点M作MH⊥x轴,垂足为H,交抛物线于M0,连接M0D,过点M0作M0K⊥y轴,垂足为K,连接KM0,设M0(b,b2+1),则H(b,0),由勾股定理表示出M0D,推出M0D=M0H,过点N作NI⊥MH,垂足为I,则四边形IHGN是矩形,得到NG=IH,根据点M0的横坐标为1,求出y的值,据此可得点N的坐标.
【解析】【分析】(1)设y=kt+b,将(1,198)、(70,60)代入求出k、b,据此可得y与t的关系式;
(2)当1≤t≤40时,w=(t+20-8)y,当40
相关试卷
这是一份浙教版数学复习阶梯训练:二次函数含解析(优生加练),共25页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。
这是一份浙教版数学复习阶梯训练:二次函数含解析(优生集训)1,共23页。试卷主要包含了综合题等内容,欢迎下载使用。
这是一份浙教版数学复习阶梯训练:二次函数含解析(优生集训)5,共20页。试卷主要包含了综合题等内容,欢迎下载使用。









