2022年（通用版）中考数学二轮复习核心专题复习专题08 几何初步及三角形相关计算（原卷+解析版）

专题08   几何初步及三角形相关计算

复习考点攻略

考点一   直线、射线、线段相关概念和性质

1．直线的性质

（1）两条直线相交，只有一个交点；

（2）经过两点有且只有一条直线，即两点确定一条直线；

（3）直线的基本事实：经过两点有且只有一条直线．

2．线段的性质：两点确定一条直线，两点之间，线段最短，两点间线段的长度叫两点间的距离．

3．线段的中点性质：若C是线段AB中点，则AC=BC=AB；AB=2AC=2BC．

4．两条直线的位置关系

在同一平面内，两条直线只有两种位置关系：平行和相交．

5．垂线的性质

（1）两条直线相交所构成的四个角中有一个角是直角，则这两条直线互相垂直，其中一条直线叫做另一条直线的垂线；

（2）①经过一点有且只有一条直线与已知直线垂直；②直线外一点与直线上各点连接的所有线段中，垂线段最短．

6．点到直线的距离：从直线外一点向已知直线作垂线，这一点和垂足之间线段的长度叫做点到直线的距离．

7. 角：有公共端点的两条射线组成的图形．

8．角平分线

（1）定义：在角的内部，以角的顶点为端点把这个角分成两个相等的角的射线

（2）角平分线的性质：①若OC是∠AOB的平分线，则∠AOC=∠BOC =∠AOB，∠AOB=2∠AOC =2∠BOC．②角平分线上的点到角两边的距离相等。

9．度、分、秒的运算方法

1°=60′，1′=60″，1°=3600″．

1周角=2平角=4直角=360°．

10．余角和补角

（1） 余角：∠1＋∠2＝90°⇔∠1与∠2互为余角；

（2）补角：∠1＋∠2＝180°⇔∠1与∠2互为补角．

（3）性质：同角（或等角）的余角相等；同角（或等角）的补角相等．

11．方向角和方位角

在描述方位角时，一般应先说北或南，再说偏西或偏东多少度，而不说成东偏北（南）多少度或西偏北（南）多少度．当方向角在45°方向上时，又常常说成东南、东北、西南、西北方向．

【例1】如图，在数轴上有A、B、C、D四个整数点（即各点均表示整数），且2AB=BC=3CD，若A、D两点表示的数分别为-5和6，且AC的中点为E，BD的中点为M，BC之间距点B的距离为BC的点N，则该数轴的原点为

A．点E B．点F

C．点M D．点N

【例2】如图，∠AOB=180°，∠BOC=80°，OD平分∠AOC，∠DOE=3∠COE，求∠BOE．

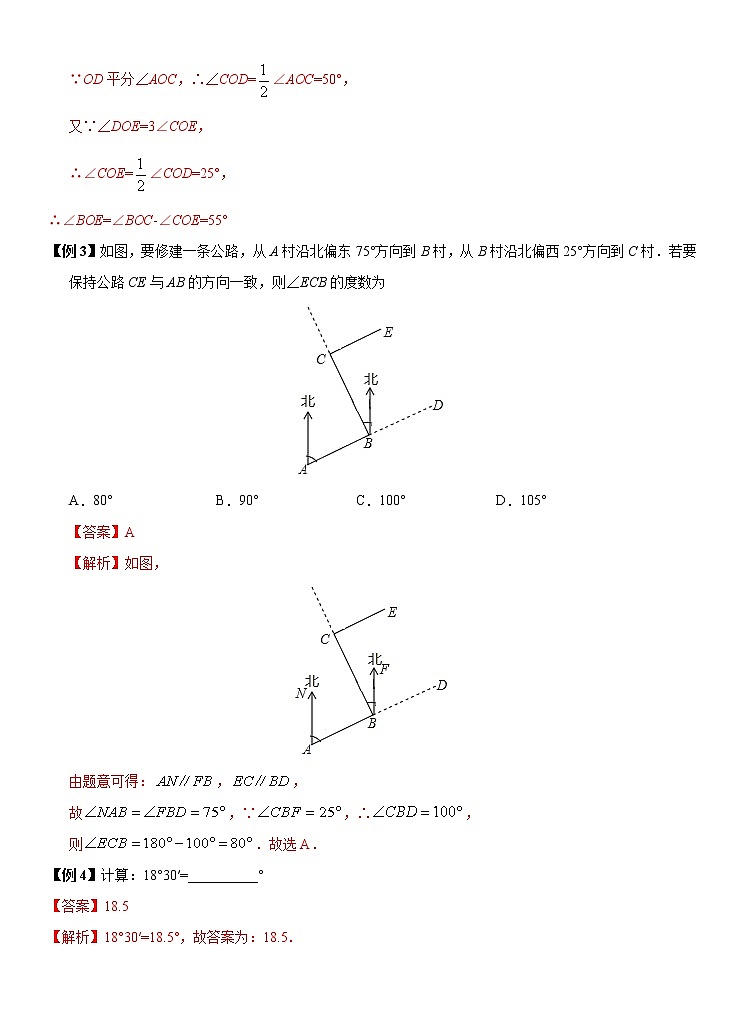
【例3】如图，要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，则∠ECB的度数为

A．80°    B．90°    C．100°    D．105°

【例4】计算：18°30′=__________° 

考点二    立体图形

1．常见的立体图形有：球、柱体和锥体．圆柱和棱柱的区别：圆柱的底面是圆，棱柱的底面是多边形；圆柱的侧面是曲面，棱柱的侧面是四边形；圆锥和棱锥的区别：圆锥的底面是圆，侧面是曲面；棱锥的底面是多边形，侧面是三角形．

2．点动成线，线动成面，面动成体，线没有粗细，点没有大小．

3．设立体图形的面数为F，顶点数为V，棱数为E，则F+V-E=2．

4．正方体的平面展开图有如下11种类型：

【例5】如图是一个正方体包装盒的表面积展开图，若在其中的三个正方形A、B、C内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在A、B、C内的三个数依次为

A．0，-2，1 B．0，1，2 

C．1，0，-2 D．-2，0，1

考点三  三角形的基本概念

(1)三角形的概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

(2)三角形的三边之间的关系：三角形两边的和大于第三边，三角形两边的差小于第三边。

【注意】三角形三边关系定理及推论的作用：

①判断三条已知线段能否组成三角形。

②当已知两边时，可确定第三边的范围。

③证明线段不等关系。

（3）三角形的高、中线、角平分线

角平分线：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线（注意与角的角平分线区分）。

中线：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。（三角形的中线平分三角形的面积）

高线：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。

（4）三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫做三角形的稳定性。三角形的这个性质在生产生活中应用很广，需要稳定的东西一般都制成三角形的形状（注意与平行四边形的不稳定性区分）。

（5）三角形的角：

①三角形的内角和等于180°。 

推论：直角三角形的两个锐角互余。有两个角互余的三角形是直角三角形。

②三角形的外角：三角形的一边与另一边的延长线组成的角，叫做三角形的外角。

③三角形内外角的关系：三角形的外角等于与它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角。

三角形的外角和等于360°。

(6)三角形的面积：三角形的面积=×底×高

【例6】以下列各组线段为边，能组成三角形的是

A．2cm，5cm，8cm B．3cm，3cm，6cm

C．3cm，4cm，5cm D．1cm，2cm，3cm

【例7】如图，在△ABC中，∠ACB=68°，若P为△ABC内一点，且∠1=∠2，则∠BPC=__________．

【例8】在△ABC中，∠BAC=115°，DE、FG分别为AB、AC的垂直平分线，则∠EAG的度数为

A．50°     B．40°    C．30°    D．25°

考点四   特殊三角形

1. 等腰三角形

（1）等腰三角形的性质定理及推论：

定理：等腰三角形的两个底角相等（简称：等边对等角）

推论1：等腰三角形顶角平分线平分底边并且垂直于底边。即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。

推论2：等边三角形的各个角都相等，并且每个角都等于60°。

（2）等腰三角形的其他性质：

①等腰直角三角形的两个底角相等且等于45°

②等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）。

③等腰三角形的三边关系：设腰长为a，底边长为b，则<a

④等腰三角形的三角关系：设顶角为顶角为∠A，底角为∠B、∠C，则∠A=180°—2∠B，∠B=∠C=

（3）等腰三角形的判定：

定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）。这个判定定理常用于证明同一个三角形中的边相等。

推论1：三个角都相等的三角形是等边三角形

推论2：有一个角是60°的等腰三角形是等边三角形。

推论3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

2. 等边三角形

（1）等边三角形的性质定理及推论：

①等边三角形是轴对称图形，其对称轴是“三边的垂直平分线” 。

②三条边上的中线、高线及三个内角平分线都相交于一点。      

③等边三角形的三个内角都等于60°。

（2）等边三角形的判定：  

①三条边都相等的三角形是等边三角形。

②三个内角都相等的三角形是等边三角形。

③有一个内角是60°的等腰三角形是等边三角形。

3.直角三角形

①在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

②在直角三角形中，斜边上的中线等于斜边的一半。

③勾股定理：如果直角三角形的两条直角边长分别为a、b，斜边长为c，那么a2+b2=c2。

④勾股定理的逆定理：如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形。

【例9】若等腰三角形的一个底角为72°，则这个等腰三角形的顶角为　　．

【例10】如图，在△ABC中，AB=AC，∠BAC=90°，BD是中线，AF⊥BD，F为垂足，过点C作AB的平行线交AF的延长线于点E．

求证：（1）∠ABD=∠FAD；

（2）AB=2CE．

【例11】如图，在等边三角形ABC中，AE=CD，AD，BE交于P点，BF⊥AD于F．

（1）求证：△ABE≌△CAD；

（2）求证：BF=PF．

第一部分 选择题

一、选择题（本题有10小题，每题3分，共30分）

1.已知AB=10，C是射线AB上一点，且AC=3BC，则BC的长为（    ）

A．2.5    B．    C．2.5或5   D．或5

2.一副三角尺按如图所示摆放，已知∠1比∠2的3倍少10°，则∠1的值为（    ）

A．20° B．70°

C．25° D．65°

3.下列各图中，可以是一个正方体的表面展开图的是（    ）

A． B． 

C． D．

4.如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的相对面上的字

A．的 B．中 

C．国 D．梦

5.将一副三角板按如图方式摆放，∠1与∠2不一定互补的是（    ）

A． B． 

C． D．

6．如图，A，B，C，D是直线L上顺次四点，M，N分别是AB，CD的中点，且MN=6 cm，BC=1 cm，则AD的长等于（    ）

A．10 cm B．11 cm 

C．12 cm D．13 cm

7. 小芳有两根长度为6cm和9cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为__________的木条．

A．2cm B．3cm

C．12cm D．15cm

8.如图，下列有四个说法，正确的个数是

①∠B＞∠ACD；②∠B+∠ACB=180°–∠A；③∠A+∠B=∠ACD；④∠HEC＞∠ B．

A．1个 B．2个 

C．3个 D．4个

9．如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为点E，DE=1，则BC=

A．    B．2    C．3    D．+2

10.如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，那么下列式子中正确的是

A．γ=2α+β B．γ=α+2β 

C．γ=α+β D．γ=180°–α–β

第二部分  填空题

二、填空题（本题有6小题，每题4分，共24分）

11.已知∠α和∠β互为补角，且∠β比∠α小30°，则∠β等于__________°．

12.如图，CE是△ABC的外角的平分线，若，则__________．

13.如图，在Rt△ABC中，∠A=90°，BD平分∠ABC交AC于D点，AB=4，BD=5，点P是线段BC上的一动点，则PD的最小值是__________．

14.如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3=__________度．

15.如图，以△ABC的顶点B为圆心，BA长为半径画弧，交BC边于点D，连接AD．若∠B＝40°，∠C＝36°，则∠DAC的大小为　    　．

16.如图,在△ABC中,AB＝AC,点D在AC上,且BD＝BC＝AD,则∠A＝______度.

第三部分   

第四部分  解答题

二、解答题（本题有7小题，共46分）

17.已知线段AB=12，CD=6，线段CD在直线AB上运动（A在B的左侧，C在D的左侧）．

（1）当D点与B点重合时，AC=__________；

（2）点P是线段AB延长线上任意一点，在（1）的条件下，求PA+PB–2PC的值；

（3）M、N分别是AC、BD的中点，当BC=4时，求MN的长．

18. 如图4—4—4所示，OB、OC是∠AOD内任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON＝α，∠BOC=β，用α、β表示∠AOD。

19.如图，在△ABC中，AB＝AC，AD⊥BC于点D．

（1）若∠C＝42°，求∠BAD的度数；

（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE＝FE．

20.如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．求证：

（1）点D在BE的垂直平分线上；

（2）∠BEC＝3∠ABE．

21.如图，中，点在边上，，将线段绕点旋转到的位置，使得，连接，与交于点

(1)求证：；

(2)若，，求的度数.

22.如图，点，，，在同一条直线上，，，，求证：．

23.如图所示，在等腰Rt△ABC中，∠CAB=90°，P是△ABC内一点，将△PAB绕A逆时针旋转90°得△DAC．

（1）试判断△PAD的形状并说明理由；

（2）连接PC，若∠APB=135°，PA=1，PB=3，求PC的长．