

2021达州高一下学期期末检测数学(理)试题含答案
展开达州市2021年普通高中一年级春季期末监测
数学试题(理科)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.
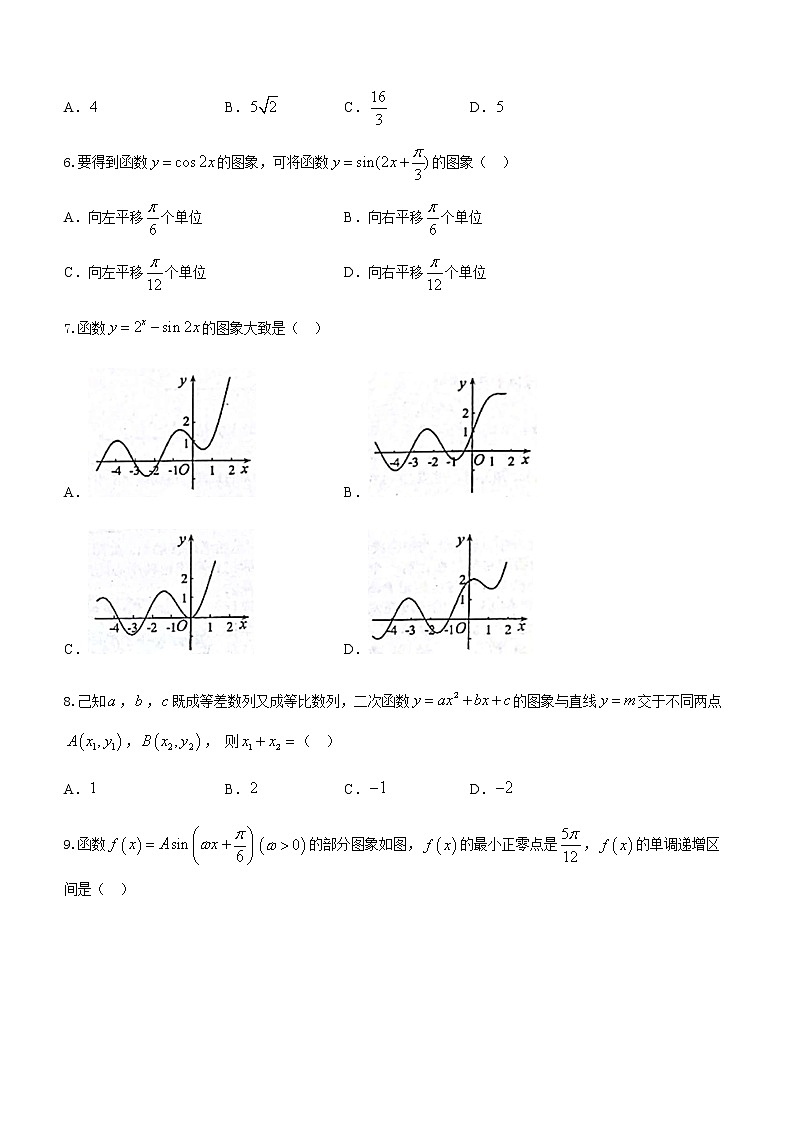
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B.
C. D.
2.三个实数,,的大小关系是( )
A. B.
C. D.
3.直线和直线的位置关系是( )
A.垂直 B.平行 C.重合 D.相交但不垂直
4.在等差数列中,,公差,则( )
A. B. C. D.
5.已知在中,,,,则( )
A. B. C. D.
6.要得到函数的图象,可将函数的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
7.函数的图象大致是( )
A. B.
C. D.
8.己知,,既成等差数列又成等比数列,二次函数的图象与直线交于不同两点,, 则( )
A. B. C. D.
9.函数的部分图象如图,的最小正零点是,的单调递增区间是( )
A. B.
C. D.
10.在中,若,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
11.在平行四边形中,,,,是线段的中点,则( )
A. B. C. D.
12.直线分别与直线和交于,两点,与交于点,为坐标原点,当到的距离最大时,( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13.在等比数列中,,,则 .
14.已知实数,满足则的最大值是 .
15.已知,, 过点且斜率为的直线与线段相交,点到直线的距离为,则实数的取值范围是_ .
16.汽车正常行驶中,轮胎上与道路接触的部分叫轮胎道路接触面.如图,一辆小汽车前左轮胎道路接触面上有一个标记, 标记到该轮轴中心的距离为.若该小汽车起动时,标记离地面的距离为,汽车以的速度在水平地面匀速行驶,标记离地面的高度(单位:)与小汽车行驶时间(单位:)的函数关系式是,其中,,,则 .
三、解答题 :共70分.解答应写出文字说明、证明过程或演算步骤.
17.下左图是台球赛实战的一个截图.白球在点处击中一球后,直线到达台球桌内侧边沿点,反弹后直线到达台球桌内侧另一边沿点,再次反弹后直线击中桌面上点处一球.以台球桌面内侧边沿所在直线为坐标轴建立如右图所示的平面直角坐标系.已知,.
(1)求直线的方程;
(2)若点的坐标是,求.(提示:直线与直线的斜率互,为相反数,.)
18.已知是数列的前项和,.
(1)求的通项公式;
(2)若,求数列前项和.
19.已知.
(1)若,对一切,恒成立,求实数的取值范围;
(2)若,,, 求的最小值.
20.已知.
(1)求函数的最小正周期;
(2)若,,求的值.
21.己知是等差数列,,是函数的两个不同零点.
(1)求数列的通项公式;
(2)若,,,都是数列前项中的项,,,是公比为的等比数列,,,成等差数列.当最大时,求.
22.如图,某人身高,他站的地点和云南大理文笔塔塔底在同水平线上,他直立时,测得塔顶的仰角(点在线段上,忽略眼睛到头顶之间的距离,下同).他沿线段向塔前进到达点,在点直立时,测得塔顶的仰角:塔尖MN的视角(是塔尖底,在线段上).
(1)求塔高;
(2)此人在线段上离点多远时,他直立看塔尖的视角最大?说明理由.
参考数据: ,,.
达州市2021年普通高中一年级春季期末检测
理科数学参考答案
一、选择题
1-5: 6-10: 11、12:
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)由,知,直线的方程是,
化简得直线方程为(或).
【方法二】由,知,直线的斜率,
直线的方程为,
化简得直线方程为(或)
(2)根据条件,直线的斜率为,
直线的方程是.
在方程中,令得点的纵坐标为.
由题意,,
直线的方程是,
,
解得(或).
18.解:(1)在中,令得,,即,
.
当时,,
,即,
.
是以为首项,以为公比的等比数列,
所以,,即.
(2),,
,
,
,
,
.
或,或.
19.解:(1)由题意可知,.
解得,,
所以,实数的取值范围是.
(2),,
.
,,
所以,,等号在时成立.
即最小值为.
20.解:(1)
,
.
所以,的最小正周期.
(2),,
.
,
,
.
.
21.解:(1)设数列的公差为.
,是函数的两个不同零点,
,.
,,
解得,,,或.
若,则,不合题意,舍.
.
所以,.
(2),
数列的前项是从到的连续个偶数.
由条件得,.
,,成等差数列,
.
.
由题意得,,即.
设,则当时,递增.因,,所以的最大值为.
,
,
.
.
22.解:(1),,
.
在中,由正弦定理得,,
又,
.
,
所以,.
(2)由(1)知,.
.
,
.
设此人应在线段上的处,,直立时,眼睛处于点,
则,,
,当且仅当,
即时,等号成立.
所以,他站在线段上到点的距离为为处时,看塔尖的视角最大.
2021达州高一下学期期末检测数学(理)试题图片版含答案: 这是一份2021达州高一下学期期末检测数学(理)试题图片版含答案
2021达州高一下学期期末检测数学(文)试题图片版含答案: 这是一份2021达州高一下学期期末检测数学(文)试题图片版含答案
2021内江高一下学期期末检测数学(理)试题扫描版含答案: 这是一份2021内江高一下学期期末检测数学(理)试题扫描版含答案,共7页。










