2021连云港赣榆一中高一下学期第二次月考数学试题含答案

这是一份2021连云港赣榆一中高一下学期第二次月考数学试题含答案，共25页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
赣榆一中高一月考数学试卷20210528
一、单选题（本大题共8小题，共40分）
1．已知复数（为虚数单位），则（ ）
A． B． C． D．
2.若，则的坐标可以是（ ）
A． B． C． D．
3．在不超过20的素数(注：如果一个大于1的整数除了1和自身外无其它正因数，则称这个整数为素数)中，随机选取2个不同的数，这两个数的和等于20的概率是（ ）
A． B． C． D．
4．某班有48名学生，在一次考试中统计出平均分为70分，方差为75，后来发现有2名同学的分数登错了，甲实得80分，却记了50分，乙得70分却记了100分，更正后平均分和方差分别是（ ）
A．70，75 B．70，50 C．75，1.04 D．65，2.35
5．已知sin= ，则cos的值为（ ）
A． B． C． D．
6．已知m，n为两条不同的直线，，为两个不同的平面，给出下列命题：
①若，则； ②若，则；
③若，则； ④若，则．
其中所有真命题的序号是（ ）
A．①② B．①②③ C．①②④ D．②
7．天气预报说，在今后的三天中，每一天下雨的概率均为，用数字0，1，2，3表示下雨，数字4，5，6，7，8，9表示不下雨，由计算机产生如下20组随机数：
977，864，191，925，271，932，812，458，569，683，431，257，394，027，556，488，730，113，537，908.由此估计今后三天中至少有一天下雨的概率为（ ）

A．0.6 B．0.7 C．0.75 D．0.8
8． 如图，中，为边上的中线，
E为延长线上一点，且，
若，，（ ）
A.2 B.4 C. D.
二、多选题（本大题共4小题，共20分）
9．某高中2020年的高考考生人数是2010年高考考生人数的1.5倍，为了更好地比较该校考生的升学情况，统计了该校2010年和2020年的高考升学率，得到如下柱状图：

则下列说法中正确的有（ ）
A． 与2010年相比，2020年一本达线人数有所减少
B．2020年二本达线率是2010年二本达线率的1.25倍
C．2010年与2020年艺体达线人数相同
D．与2010年相比，2020年不上线的人数有所增加
10．甲乙两个质地均匀且完全一样的四面体，每个面都是正三角形，甲四个面上分别标有数字1，2，3，4，乙四个面上分别标有数字5，6，7，8，同时抛掷这两个四面体一次，记事件为“两个四面体朝下一面的数字之和为奇数”，事件为“甲四面体朝下一面的数字为奇数”，事件为“乙四面体朝下一面的数字为偶数”，则下列结论正确的是（ ）
A． B．
C． D．
11.在中，角A，B，C所对的边分别为a，b，c，给出下列命题，其中正确的命题为（ ）
A．若，则；
B．若，则满足条件的有两个；
C．若，则是钝角三角形；
D．存在角A，B，C，使得成立；
12．如图，在正方体中，点在线段上运动，则（ ）

A．直线平面
B．二面角的大小为
C．三棱锥的体积为定值
D．异面直线与所成角的取值范围是


三、填空题（本大题共4小题，共20分）
16题

15题


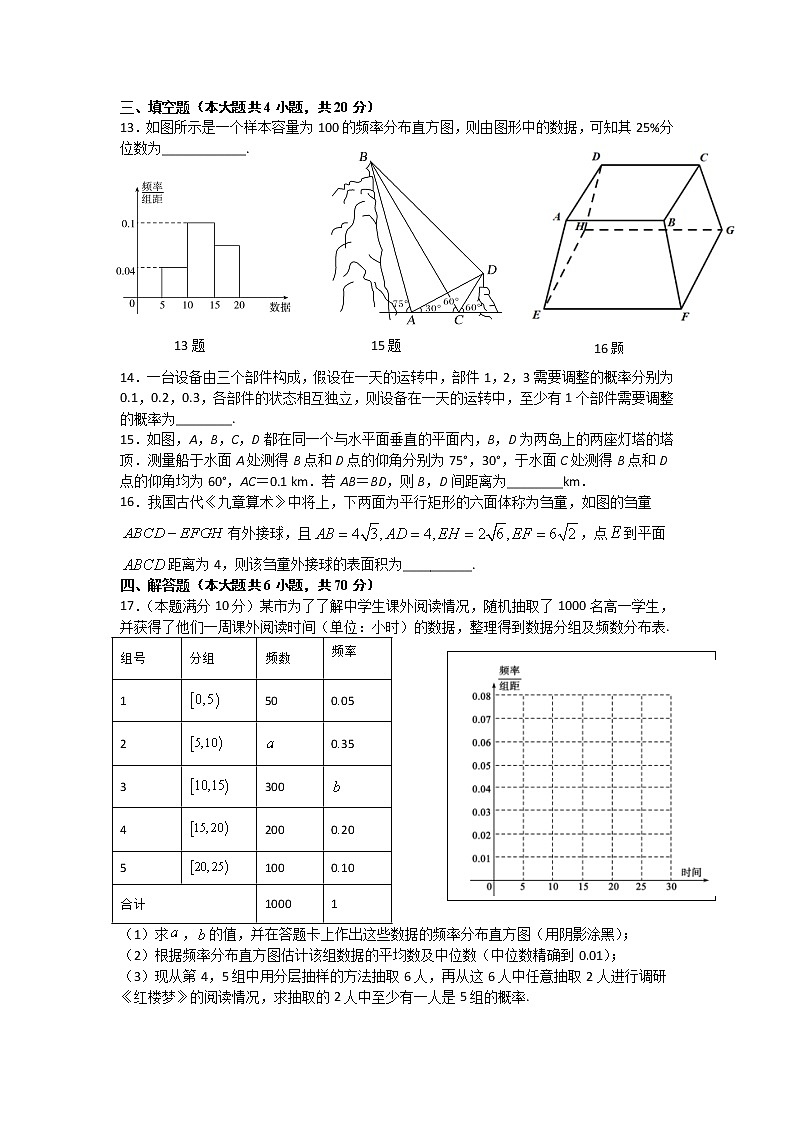
13．如图所示是一个样本容量为100的频率分布直方图，则由图形中的数据，可知其25%分位数为____________.
13题











14．一台设备由三个部件构成，假设在一天的运转中，部件1，2，3需要调整的概率分别为0.1，0.2，0.3，各部件的状态相互独立，则设备在一天的运转中，至少有1个部件需要调整的概率为________.
15．如图，A，B，C，D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶．测量船于水面A处测得B点和D点的仰角分别为75°，30°，于水面C处测得B点和D点的仰角均为60°，AC＝0.1 km．若AB＝BD，则B，D间距离为________km．
16．我国古代《九章算术》中将上，下两面为平行矩形的六面体称为刍童，如图的刍童有外接球，且，点到平面距离为4，则该刍童外接球的表面积为__________.
四、解答题（本大题共6小题，共70分）
17．（本题满分10分）某市为了了解中学生课外阅读情况，随机抽取了1000名高一学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.
组号
分组
频数

频率
1

50
0.05
2


0.35
3

300

4

200
0.20
5

100
0.10
合计
1000
1
（1）求，的值，并在答题卡上作出这些数据的频率分布直方图（用阴影涂黑）；
（2）根据频率分布直方图估计该组数据的平均数及中位数（中位数精确到0.01）；
（3）现从第4，5组中用分层抽样的方法抽取6人，再从这6人中任意抽取2人进行调研《红楼梦》的阅读情况，求抽取的2人中至少有一人是5组的概率.

18. （本题满分12分）如图，在四棱锥中，底面是矩形．（1）设为上靠近的三等分点，为上靠近的三等分点．求证：平面．
（2） 设是上靠近点的一个三等分点，
试问：在上是否存在一点，使平面
成立？若存在，请予以证明；若不存在，说明理由．

19．（本题满分12分）
在①②③三个条
件中选一个，补充在下面的横线处，然后解答问题．在中，角A，B，C所对的边分别是a，b，c，设的面积为S，已知________．
（1）求角C的值；（2）若，点D在边上，为的平分线，的面积为，求边长a的值．
20.（本题满分12分）如图，在四棱锥P—ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA＝AB，E为线段PB的中点．
（1）若F为线段BC的中点，求异面直线EF与PD所成角的余弦值；
20题


22题
（2）证明：点F在线段BC上移动时，△AEF始终为直角三角形．








21题




21.（本题满分12分）市政府拟在蝶湖建一个旅游观光项目，设计方案如下：
如图所示的圆是圆形湖的边界，沿线段建一个观景长廊，其中 是观景长廊的四个出入口且都在圆 上，已知： 百米， 百米,在湖中处和湖边处各建一个观景亭，且它们关于直线 对称,在湖面建一条观景桥观景亭的大小、观景长廊、观景桥的宽度均忽略不计，设Ð．
（1）若观景长廊 百米，，求由观景长廊所围成的四边形内的湖面面积；
（2）若 百米且规划建亭点P 在三角形 区域内（不包括边界），试判断四边形内湖面面积是否有最大值？若有，求出最大值，并写出此时的值；若没有，请说明理由．
22.（本题满分12分）已知四边形．现将沿BD边折起，使得平面平面BCD，．点P为线段的中点．请你用几何法解决下列问题：
（1）求证：平面ACD；（2）若M为CD的中点，求MP与平面BPC所成角的正弦值．
赣榆一中高一月考数学试卷20210528
一、单选题（本大题共8小题，共40分）
1．已知复数（为虚数单位），则（ ）
A． B． C． D．
【答案】D
【分析】
根据复数的除法运算法则，结合复数的模的公式进行求解即可.
【详解】
因为，
所以，
故选：D
2.若，则的坐标可以是（ ）
A． B． C． D．
【答案】C
【解析】四个选项模长均为，设，因为，所以，
故选:C.

3．在不超过20的素数(注：如果一个大于1的整数除了1和自身外无其它正因数，则称这个整数为素数)中，随机选取2个不同的数，这两个数的和等于20的概率是（ ）
A． B． C． D．
【答案】A
【解析】不超过20的素数有，从中任取2个，有种取法，
其中满足和等于20的取法有共2，
根据古典概型的概率公式得所求概率为.故选：A

4．某班有48名学生，在一次考试中统计出平均分为70分，方差为75，后来发现有2名同学的分数登错了，甲实得80分，却记了50分，乙得70分却记了100分，更正后平均分和方差分别是（ ）
A．70，75 B．70，50
C．75，1.04 D．65，2.35
【答案】B
【解析】因甲少记了30分，乙多记了30分，故平均分不变，设更正后的方差为s2，由题意得，
s2＝[(x1－70)2＋(x2－70)2＋…＋(80－70)2＋(70－70)2＋…＋(x48－70)2]，而更正前有：
75＝[(x1－70)2＋(x2－70)2＋…＋(50－70)2＋(100－70)2＋…＋(x48－70)2]，
化简整理得s2＝50.故选:B.
5．已知sin= ，则cos的值为（ ）
A． B． C． D．
【答案】C
【分析】
已知条件由诱导公式可化为，再由余弦的二倍角公式可解．
【详解】
解：，
，
．
故选：．

6．已知m，n为两条不同的直线，，为两个不同的平面，给出下列命题：
①若，则； ②若，则；
③若，则； ④若，则．
其中所有真命题的序号是（ ）
A．①② B．①②③ C．①②④ D．②
答案：A 易知①②正确；对于③，m，n可能平行，也可能异面，所以③错；对于④，n可能平行于，也可能n在平面内，所以④错，选A．


7．如图，中，为边上的中线，E为延长线上一点，且，若，，（ ）

A．2 B．4 C． D．
【答案】D
【解析】又因为，所以，解得，所以.故选D.



8．天气预报说，在今后的三天中，每一天下雨的概率均为，用数字0，1，2，3表示下雨，数字4，5，6，7，8，9表示不下雨，由计算机产生如下20组随机数：
977，864，191，925，271，932，812，458，569，683，
431，257，394，027，556，488，730，113，537，908.
由此估计今后三天中至少有一天下雨的概率为（ ）
A．0.6 B．0.7 C．0.75 D．0.8
【答案】B
【解析】代表今后三天都不下雨的随机数有977，864，458，569，556，488，共6组，记“今后三天中至少有一天下雨”为事件，“今后三天都不下雨”为事件，则与为对立事件.所以，故选：B.


二、多选题（本大题共4小题，共20分）
9．某高中2020年的高考考生人数是2010年高考考生人数的1.5倍，为了更好地比较该校考生的升学情况，统计了该校2010年和2020年的高考升学率，得到如下柱状图：

则下列说法中正确的有（ ）
A．与2010年相比，2020年一本达线人数有所减少
B．2020年二本达线率是2010年二本达线率的1.25倍
C．2010年与2020年艺体达线人数相同
D．与2010年相比，2020年不上线的人数有所增加
【答案】BD
【分析】
根据柱状图中的数据求解.
【详解】
设2010年高考考生人数为a，则2020年的高考考生人数是的1.5a，
A. 2010年一本达线人数为0.28a，2020年一本达线人数a，故错误；
B. 2020年二本达线率是，2010年二本达线率是，，故正确；
C. 2010年艺体达线人数0.08a， 2020年艺体达线人数，故错误；
D.与2010年不上线的人数0.32a,相比，2020年不上线的人数,故正确；
故选：BD
10．甲乙两个质地均匀且完全一样的四面体，每个面都是正三角形，甲四个面上分别标有数字1，2，3，4，乙四个面上分别标有数字5，6，7，8，同时抛掷这两个四面体一次，记事件为“两个四面体朝下一面的数字之和为奇数”，事件为“甲四面体朝下一面的数字为奇数”，事件为“乙四面体朝下一面的数字为偶数”，则下列结论正确的是（ ）
A． B．
C． D．
【答案】ABD
【解析】由已知，，
由已知有，，，
所以，则A正确；
，则B正确；
事件、、不相互独立，故错误，即C错误
，则D正确；综上可知正确的为ABD.故选:ABD．

11.在中，角A，B，C所对的边分别为a，b，c，给出下列命题，其中正确的命题为（ ）
A．若，则；
B．若，则满足条件的有两个；
C．若，则是钝角三角形；
D．存在角A，B，C，使得成立；
【答案】ABC
【解析】A.若，，由正弦定理可得：，则，所以该选项正确；
B. 若，，，则，因此满足条件的有两个，所以该选项正确；
C. 若，则，，，，是钝角三角形，所以该选项正确；
D. 由于当时，，，所以该选项不正确.故选：ABC

12．如图，在正方体中，点在线段上运动，则（ ）

A．直线平面
B．二面角的大小为
C．三棱锥的体积为定值
D．异面直线与所成角的取值范围是
【答案】AC
【解析】如图，

在A中，∵A1C1⊥B1D1，A1C1⊥BB1，B1D1∩BB1＝B1，
∴A1C1⊥平面BB1D1，∴A1C1⊥BD1，同理，DC1⊥BD1，
∵A1C1∩DC1＝C1，∴直线BD1⊥平面A1C1D，故A正确；
在B中，由正方体可知平面不垂直平面,故B错误；
在C中，∵A1D∥B1C，A1D⊂平面A1C1D，B1C⊄平面A1C1D，
∴B1C∥平面 A1C1D，
∵点P在线段B1C上运动，∴P到平面A1C1D的距离为定值，
又△A1C1D的面积是定值，∴三棱锥P﹣A1C1D的体积为定值，故C正确；
在D中，当点P与线段的端点重合时, 异面直线与所成角取得最小值为,故异面直线AP与A1D所成角的取值范用是，故D错误.故选：AC


三、填空题（本大题共4小题，共20分）
13．如图所示是一个样本容量为100的频率分布直方图，则由图形中的数据，可知其25%分位数为____________.

【答案】10.5
【解析】由图可知第一组的频率为，
前两组的频率之和为，
则可知其25%分位数在内，设为，
则，解得.故答案为：10.5.
14．一台设备由三个部件构成，假设在一天的运转中，部件1，2，3需要调整的概率分别为0.1，0.2，0.3，各部件的状态相互独立，则设备在一天的运转中，至少有1个部件需要调整的概率为________.
【答案】0.496
【分析】
先求没有1个部件需要调整的概率，再用1减即可.
【详解】
设分别为部件1，2，3需要调整的事件，则至少有1个部件需要调整的概率为

故答案为：0.496
15．如图，A，B，C，D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶．测量船于水面A处测得B点和D点的仰角分别为75°，30°，于水面C处测得B点和D点的仰角均为60°，AC＝0.1 km．若AB＝BD，则B，D间距离为________km．

【答案】
【分析】
在△ABC中，应用正弦定理求，由BD＝AB，即知B，D间距离.
【详解】
在△ABC中，∠BCA＝60°，∠ABC＝75°－60°＝15°，AC＝0.1 km，
由正弦定理，得：，
∴ (km)，又BD＝AB，
∴km．
故答案为：
16．我国古代《九章算术》中将上，下两面为平行矩形的六面体称为刍童，如图的刍童有外接球，且，点到平面距离为4，则该刍童外接球的表面积为__________.

【答案】
【分析】
由已知得，球心在上下底面中心的连线上，该连线与上下底面垂直，球心必在该垂线上，然后根据，利用直角三角形与直角三角形，即可列出外接球半径的方程，求解即可.
【详解】
假设为刍童外接球的球心，连接、交于点，连接、交于点，由球的几何性质可知、、在同一条直线上，

由题意可知，平面，平面，，
设，
在中，，
在矩形中，，
，
，
在中，，
在矩形中，，，，
设外接球半径，
，解得，
则，即，则该刍童的外接球半径为
该刍童外接球的表面积为：，
故答案为：.


四、解答题（本大题共6小题，共70分）
17．某市为了了解中学生课外阅读情况，随机抽取了1000名高一学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.
组号
分组
频数
频率
1

50
0.05
2


0.35
3

300

4

200
0.20
5

100
0.10
合计
1000
1

（1）求，的值，并在答题卡上作出这些数据的频率分布直方图（用阴影涂黑）；
（2）根据频率分布直方图估计该组数据的平均数及中位数（中位数精确到0.01）；
（3）现从第4，5组中用分层抽样的方法抽取6人，再从这6人中任意抽取2人进行调研《红楼梦》的阅读情况，求抽取的2人中至少有一人是5组的概率.
【解析】（1）根据频率分布直方表，可得，
解得，，
频率分布直方图，如图所示：

（2）该组数据的平均数：，
由题图可知，中位数应在10至15之间，设中位数为，
则，解得，故中位数的估计值为11.67.
（3）从第4，5组抽取的人数分别为4，2，第4组的4人，
设为，，，，第5组的2人，设为，，
则从该6人中选出2人的基本事件有，，，，，，，，，，，，，，，共15种，
其中都是第4组的基本事件有，，，，，，共6种，
所以至少有一名学生是5组的概率.

18.如图，在四棱锥中，底面是矩形．

（1）设为上靠近的三等分点，为上靠近的三等分点．求证：平面．
（2）设是上靠近点的一个三等分点，试问：在上是否存在一点，使平面成立？若存在，请予以证明；若不存在，说明理由．
【解析】（1）如图，取上靠近的三等分点，连接，
中，，
则又平面，平面，
平面，同理，平面，又，
∴平面平面，又平面，
∴平面．

（2）存在中点，使平面成立．
取中点，连，使，连．

是矩形，是的中点，
又是上靠近点的一个三等分点，且是中点，
是的中点，
中，，
又平面，平面，
平面，
故在上是存在中点，使平面成立．





19．在①②③三个条件中选一个，补充在下面的横线处，然后解答问题．在中，角A，B，C所对的边分别是a，b，c，设的面积为S，已知________．
（1）求角C的值；
（2）若，点D在边上，为的平分线，的面积为，求边长a的值．
【解析】（1）选①，由余弦定理得，
整理得，所以，又，故.
选②，因为，，
故，可得，又，故.
选③，可得，
所以，又，所以，故.
（2）在中，因为是的平分线，且，设，所以

，又，联立以上两式得：
，又，解得.




20.（12分）如图，在四棱锥P—ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA＝AB，E为线段PB的中点．

（1）若F为线段BC的中点，求异面直线EF与PD所成角的余弦值；
（2）证明：点F在线段BC上移动时，△AEF始终为直角三角形．
【答案】（1）；（2）证明见解析.
【分析】
（1）由中位线定理得，得∠DPC是异面直线EF与PD的所成角或其补角．利用线面垂直的判定与性质定理证明，在直角三角形中求得∠DPC的余弦；
（2）由线面垂直的性质得，从而可证与平面垂直，即证得，然后利用证明与平面垂直即得，证得结论成立．
【详解】
（1）在△PBC中，E为线段PB的中点，F为线段BC的中点，所以EF∥PC，
所以∠DPC是异面直线EF与PD的所成角或其补角．
因为PA⊥底面ABCD，CDÌ平面ABCD，所以PA⊥CD．
因为ABCD为正方形，所以AD⊥CD，
又因为PA∩AD＝A，PA，ADÌ平面PAD，所以CD⊥平面PAD．
因为PDÌ平面PAD，所以PD⊥CD．
在Rt△PAD中，PA＝AD，所以PD＝AD，
因为CD＝AD，所以在Rt△PCD中，PD＝CD，PC＝CD，
所以cos∠DPC＝＝，
即异面直线EF与PD所成角的余弦值为．
（2）证明：因为PA⊥底面ABCD，BCÌ平面ABCD，所以PA⊥BC．
因为ABCD为正方形，所以AB⊥BC，
又因为PA∩AB＝A，PA，ABÌ平面PAB，所以BC⊥平面PAB．
因为AEÌ平面PAB，所以AE⊥BC．
因为PA＝AB，E为线段PB的中点，所以AE⊥PB，
又因为PB∩BC＝B，PB，BCÌ平面PBC，所以AE⊥平面PBC．
又因为EFÌ平面PBC，所以AE⊥EF，
所以点F在线段BC上移动时，△AEF以∠AEF为直角的直角三角形．
【点睛】
本题考查求异面直线所成的角，考查用线面垂直证明线线垂直，求异面直线所成的角，一般有三步：作证算，证明空间线面平行与垂直时注意定理的条件要全面，列举出所有条件后可得结论．本题考查学生的空间想象能力，逻辑推理能力，运算求解能力．属于中档题．
21


22.已知四边形．现将沿BD边折起，使得平面平面BCD，．点P为线段的中点．请你用几何法解决下列问题：

（1）求证：平面ACD；
（2）若M为CD的中点，求MP与平面BPC所成角的正弦值．
【解析】，为等边三角形，为中点．

取中点﹐连接则，
平面平面平面平面平面
又，平面
平面又且
平面.
由可知，，所以，
作于H，连接BM，因为平面所以平面又点P为线段的中点，所以，　

又M为CD的中点，所以，所以，
在中，，所以满足，所以，所以，
设点M到面PCB的距离为，，所以，解得，
又，设MP与平面BPC所成角为，所以，
所以MP与平面BPC所成角的正弦值．