2020-2021学年7.3.5 已知三角函数值求角教案配套课件ppt

这是一份2020-2021学年7.3.5 已知三角函数值求角教案配套课件ppt，共13页。PPT课件主要包含了已知三角函数值求角，解唯一，角的范围决定解的个数，学习目标，改为在R上呢，当堂演练，问题探究，当堂小结，当堂达标，课后作业等内容，欢迎下载使用。

( )
（口答）求下列三角函数值
sinX= ,如何求角X？
1.掌握已知三角函数值求角的方法,会由已知的三角函数值求角,并会用符号arcsin y,arccs y,arctan y表示角.2.能根据三角函数值与角之间的对应关系求其在区间[0,2π]上对应的角.3.通过角与三角函数值之间的互求，培养灵活的解题能力，树立对立统一的观点.
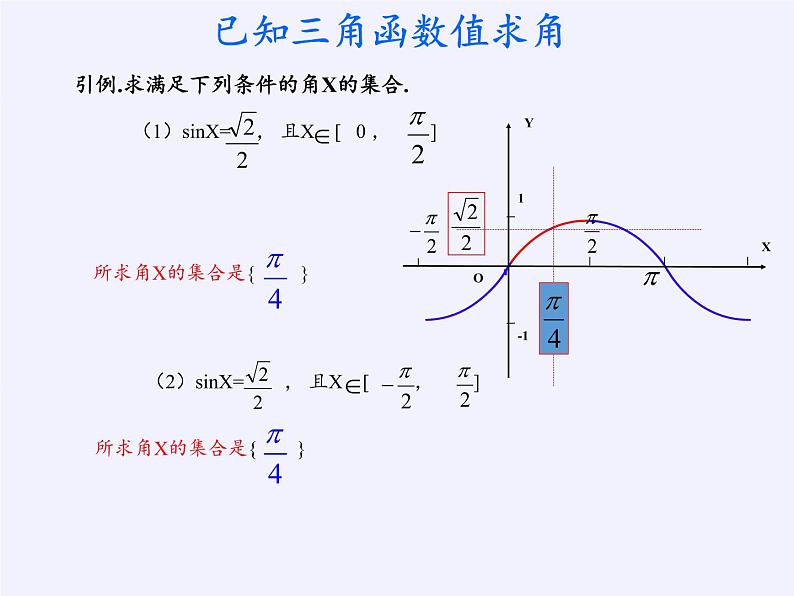
引例.求满足下列条件的角X的集合.
（1）sinX= ， 且X [ 0 ， ]
所求角X的集合是{ }
（2）sinX= ， 且X [ ， ]
所求角X的集合是{ }
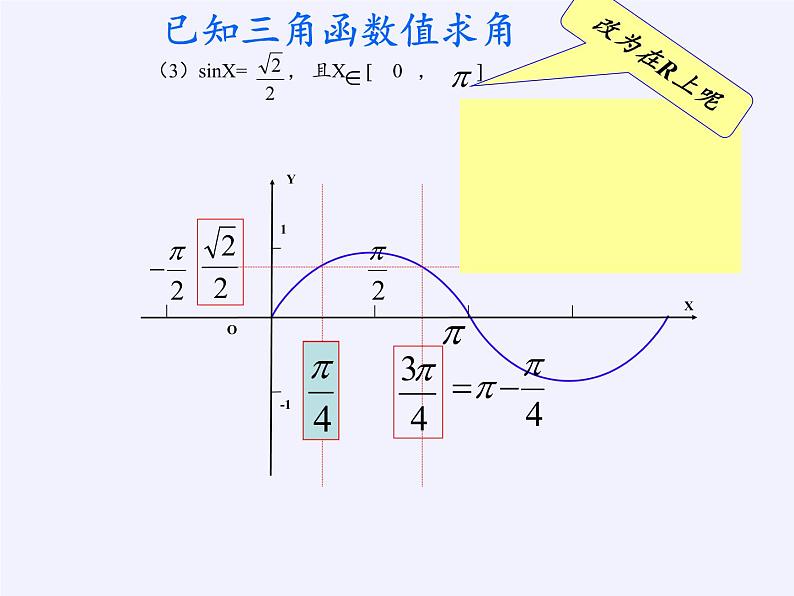
（3）sinX= ， 且X [ ， ]
可知在 X [0， ]上 符合条件的角有且只有两个，即第三象限的角 + = 或第四象限的角 - = .
思考1 已知sinX= ，且X [ 0 ， ] ，求X的取值集合
sinX= < 0 且X [ 0 ， ] ,
X是第三，四象限的角,
因为sin( + )=sin( - )=-sin = ,
于是所求的角X的集合是{ ， }
而满足条件sinX= 的锐角为 ,
找锐角时，如果正弦值为负，则求出与其绝对值对应的锐角 ；
如果正弦值为正，则可直接求出对应的锐角 .
满足条件sinX= 0.5 的锐角X =
思考2： 已知sinX= - 0.3332,且X [ 0 ， ] ，求角X的取值集合.
上题答案可以写成：{ + arcsin 0.3332 , - arcsin0.3332 }
满足条件sinX= 0.3458 的锐角X =
定义: 一般地，对于正弦函数y=sinx，如果已知函数值y(y [ -1 ，1 ])， 那么在 [ , ]上有唯一的x值和它对应，记为x=arcsin y(其中-1≤y ≤1, ).
例1：已知sinx=a，其中x ∈(0,2π),a ∈(-1,1),求角x的集合。
解： 0＜ a ＜1时，x ∈{arcsina, π-arcsina}; a=0时,x ∈{π}; -1 ＜a ＜0时，x ∈{π-arcsin|a|, 2π-arcsin|a|}
解题步骤归纳：1、找锐角；2、看范围；3、写集合。
思考3 例2：已知csx= ,且x ∈[0,2π）求角x的集合.
思考4 例3：已知tanx= ,且 x ∈（ , ）求角x的集合.
定义：如果我们限定x在区间[0, π]内取值，那么对区间[-1，1]上的任意一个值y，x只有唯一值与之对应。在区间[0, π ]上符合条件csx=y(-1 ≤y ≤1))的角x，记为x=arccsy.
例2答案｛ ，π+ ｝
定义：一般地，如果tanx=y(y ∈R),且x ∈( , ),那么对每一个正切值y，在开区间（ ， ）内，有且只有一个角x，使tanx=y,符合上述条件的角x，记为x=arctany,x ∈( , )
同学们我们本节课共同探讨了哪些知识？
2、求下列各式中的x(-π≤x≤ π)
(1)sinx= ;(2)csx= ; (3)tanx=-3.415; (4)tanx=-1.
3、若x= 是方程2cs(x+α)=1的解，其中α ∈（0，2π），则α=
1、教材60、61页A组题3题，5题 教材63页9题，10题2、教材61页A组4题，B组1题、2题