华师大版九年级下册3. 圆周角教学课件ppt

这是一份华师大版九年级下册3. 圆周角教学课件ppt，共29页。PPT课件主要包含了学习目标，复习引入，知识点等内容，欢迎下载使用。

1、掌握直径所对的圆周角是直角；直角所对的弦是直径。2、掌握圆周角的定义。3、掌握圆周角和圆心角的关系：同弧或等弧所对的圆周角。4、掌握圆内接四边形对角互补。
在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等。
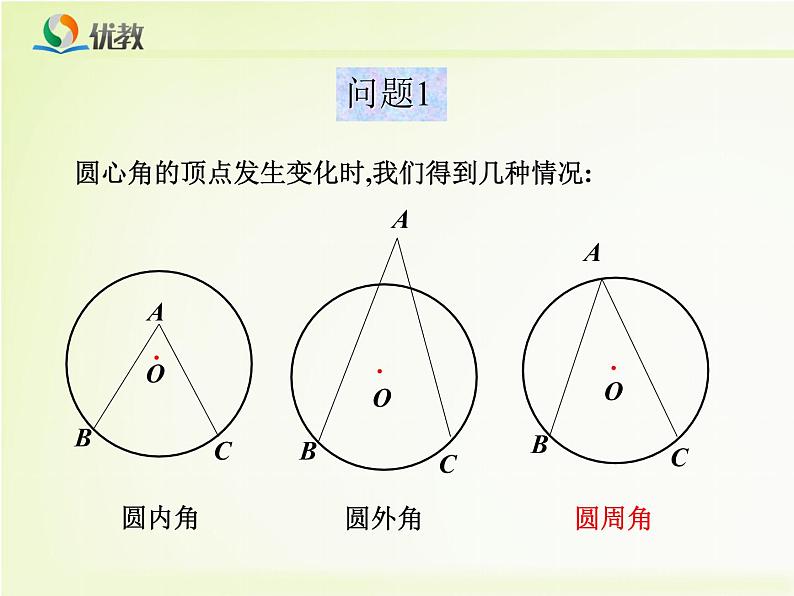
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？
1、你能说出圆周角的定义吗？举例说明。2、
如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？
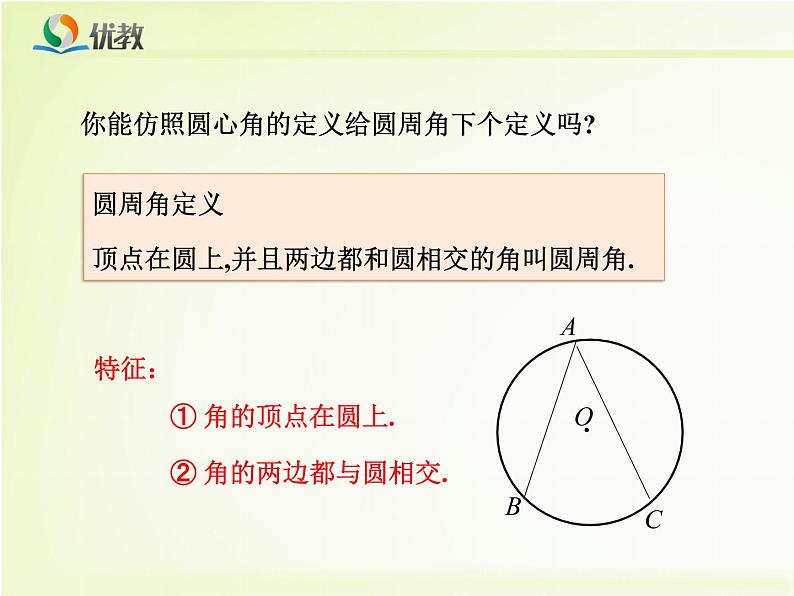
圆心角的顶点发生变化时,我们得到几种情况:
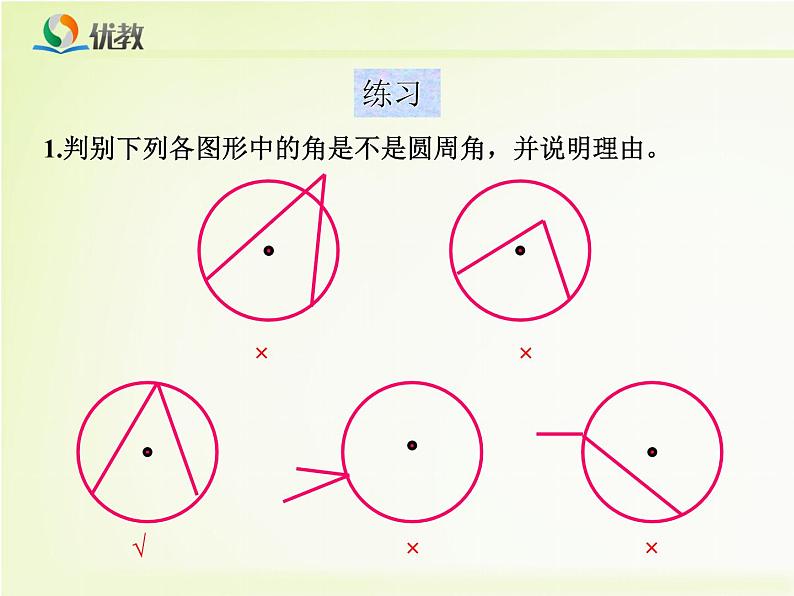
你能仿照圆心角的定义给圆周角下个定义吗?
圆周角定义顶点在圆上,并且两边都和圆相交的角叫圆周角.
1.判别下列各图形中的角是不是圆周角，并说明理由。
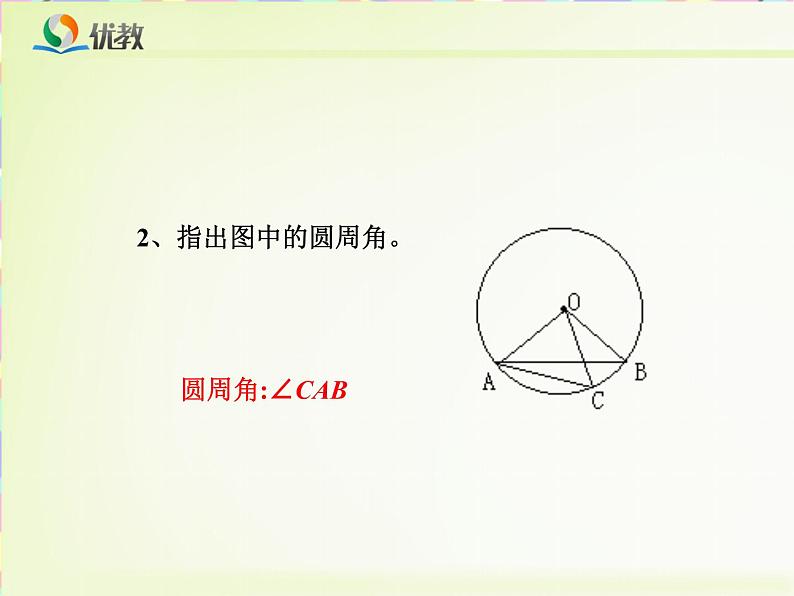
2、指出图中的圆周角。
如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？
解：∠ACB是直角（90°）∵OA=OB=OC∴ ∠OAC=∠OCA=∠OCB又∵∠OAC+∠OBC+∠ACB=180°∴∠ACB=∠OCA+∠OCB=180°÷2=90°
半圆或直径所对的圆周角都相等，都等于90°.
90°的圆周角所对的弦是圆的直径
1.同一条弧你能画多少个圆周角?多少个圆心角?用量角器量一量这些圆周角你有何发现？
2.再用量角器量出圆心角的度数,你有何发现呢?
3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况?
4、你能证明圆周角与圆心角之间的数量关系吗?
画一个圆心角，然后再画同弧所对的圆周角.
发现:一条弧所对的圆周角等于它所对的圆心角的一半.
发现:在同圆(或等圆)中,同弧或等弧所对的圆周角相等
分三种情况来证明：（1）圆心在∠BAC的一边上
（2）圆心在∠BAC的内部.
（3）圆心在∠BAC的外部.
在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。
4、在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x= ；
1、你能说出外接圆的定义吗？举例说明。
2、你能说出内接多边形的定义吗？举例说明。
3、你能猜想图中∠A与∠C的关系吗？4、你能说出问题3的证明过程吗？
圆内接多边形：如果一个圆经过一个多边形的各个顶点，这个圆叫做这个多边形的外接圆，这个多边形就叫做圆内接多边形．
圆周角定理的推论2(圆内接四边形的性质)：圆内接四边形的对角互补.
1、下列说法正确的是(　　)A．在圆内部的多边形叫做圆内接多边形B．过四边形的四个顶点的圆叫做这个四边形的外接圆C．任意一个四边形都有外接圆D．一个圆只有唯一一个内接四边形
2、下列多边形中一定有外接圆的是(　　)A．三角形 B．四边形C．五边形 D．六边形
3、下列命题中，不正确的是(　　)A．矩形有一个外接圆B．不在同一直线上的三点确定一个圆C．菱形有一个外接圆D．任何一个三角形都有一个外接圆
4、如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD＝105°，则∠DCE的大小是________．
5、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线上一点，∠CBE＝40°，则∠AOC等于(　　)A．20° B．40° C．80° D．100°
(2015·青岛)如图，圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠A＝55°，∠E＝30°,则∠F＝________.
（2018江苏中考） 如图，AB为⊙O的直径，CD是⊙O的弦，∠ADC=35∘，则∠CAB的度数为（　　）
（2010河南中考）如图，AB切⊙O于点A，BO交⊙O于点C，点D是弧CmA上异于点C、A的一点，若∠ABO=32∘，∠ADC的度数是 。
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等，都等于90°90°的圆周角所对的弦是圆的直径
4、圆内接四边形的角的关系：对角互补，若四边形ABCD为⊙O的内接四边形， 则∠A＋∠C＝180°，∠B＋∠D＝180°.