数学八年级上册第三章 勾股定理综合与测试学案
展开知识定位
掌握勾股定理的直接应用;
掌握构造勾股定理法。
掌握勾股定理的综合应用
知识梳理1:勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。公式的变形:a2 = c2- b2, b2= c2-a2 。
勾股定理在西方叫毕达哥拉斯定理,也叫百牛定理。它是直角三角形的一条重要性质,揭示的是三边之间的数量关系。它的主要作用是已知直角三角形的两边求第三边。勾股定理是一个基本的几何定理,它是用代数思想解决几何问题的最重要的工具之一,是数形结合的纽带之一。
勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
①已知的条件:某三角形的三条边的长度.②满足的条件:最大边的平方=最小边的平方+中间边的平方.③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
知识梳理2
勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。注意:①勾股数必须是正整数,不能是分数或小数。②一组勾股数扩大相同的正整数倍后,仍是勾股数。常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,13
判断直角三角形:如果三角形的三边长满足,那么这个三角形是直角三角形。(经典直角三角形:勾三、股四、弦五)
其他方法:(1)有一个角为的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:
(1)确定最大边(不妨设为);
(2)若,则是以为直角的三角形;
若,则此三角形为钝角三角形(其中为最大边);
若,则此三角形为锐角三角形(其中为最大边)
【题目】 若直角三角形两直角边的比是3:4,斜边长是20,求此直角三角形的面积。
【题目】 如图,公路和公路在点处交汇,且,点处有一所中学,=。假设拖拉机行驶时,周围以内会受到噪音的影响,那么拖拉机在公路上沿PN方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为,那么学校受影响的时间为多少秒?
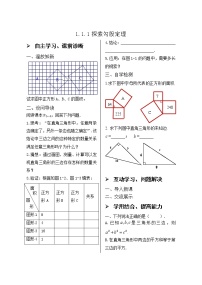
【题目】 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是______________。
【题目】 如图所示,是等腰直角三角形,,是斜边的中点,、分别是、边上的点,且,若,.求线段的长。
【题目】已知中,,,,求、、的值。
【题目】等边三角形的边长为2,求它的面积
【题目】直角三角形周长为,斜边长为,求直角三角形的面积
【题目】若直角三角形的三边长分别是,,,求。
习题演练
【题目】 以下列各组数为边长,能组成直角三角形的是( )
A、8,15,17 B、4,5,6 C、5,8,10 D、8,39,40
【题目】如图学校有一块长方形花园,有极少数人为了避开拐角而走“捷径”,在花园内走出了一条“路”。他们仅仅少走了__________步路(假设2步为1m),却踩伤了花草。
.
【题目】如图中的虚线网格我们称之为正三角形网格,它的每一个小三角形都是边长为1的正三角形,这样的三角形称为单位正三角形。
(1)直接写出单位正三角形的高与面积。
(2)图中的平行四边形含有多少个单位正三角形?平行四边形的面积是多少?
(3)求出图中线段的长(可作辅助线)。
【题目】如图所示,折叠矩形的一边,使点落在边的点处,已知,,求的长。
【题目】如图所示,在一次夏令营活动中,小明从营地点出发,沿北偏东方向走了到达点,然后再沿北偏西方向走了到达目的地点.
(1)求、两点之间的距离.
(2)确定目的地在营地的什么方向.
【题目】国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进行电网改造,某地有四个村庄、、、,且正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分.请你帮助计算一下,哪种架设方案最省电线.
【题目】作长为、、的线段.
【题目】如果的三边分别为、、,且满足,判断的形状.
【题目】如图,, 则的长是多少?
【题目】如图,已知:,,于.
求证:。
【题目】已知:如图,,,.求:四边形的面积.
【题目】.如图正方形,为中点,为上一点,且。请问与是否垂直?请说明。
初中数学苏科版八年级上册3.1 勾股定理导学案: 这是一份初中数学苏科版八年级上册3.1 勾股定理导学案,文件包含第12讲勾股定理教师版-数学八上同步精品讲义苏科版docx、第12讲勾股定理学生版-数学八上同步精品讲义苏科版docx等2份学案配套教学资源,其中学案共41页, 欢迎下载使用。
苏科版八年级上册第三章 勾股定理综合与测试导学案及答案: 这是一份苏科版八年级上册第三章 勾股定理综合与测试导学案及答案,共15页。学案主要包含了股四等内容,欢迎下载使用。
人教版八年级下册第十七章 勾股定理综合与测试学案及答案: 这是一份人教版八年级下册第十七章 勾股定理综合与测试学案及答案,文件包含人教版八年级数学下册同步讲义第08课勾股定理全章复习与巩固教师版docx、人教版八年级数学下册同步讲义第08课勾股定理全章复习与巩固学生版docx等2份学案配套教学资源,其中学案共37页, 欢迎下载使用。