《二次函数》复习参考课件

这是一份《二次函数》复习参考课件，共17页。

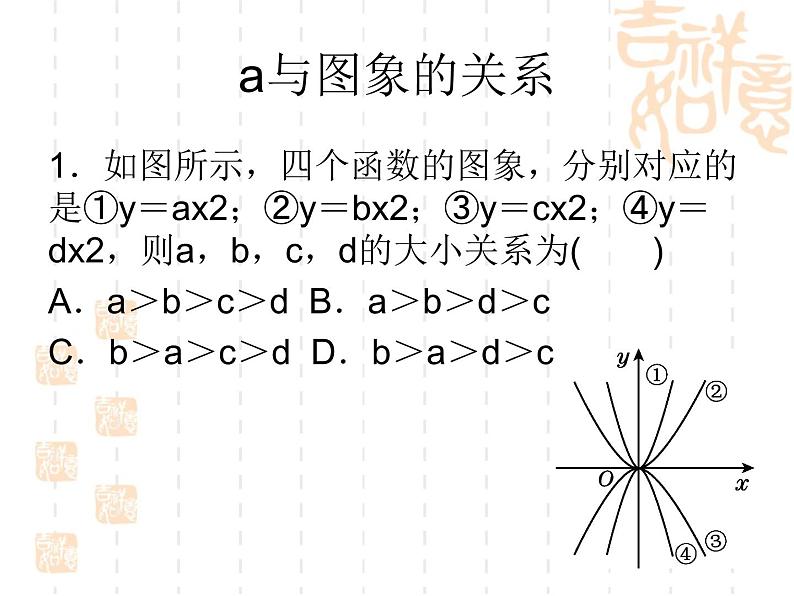
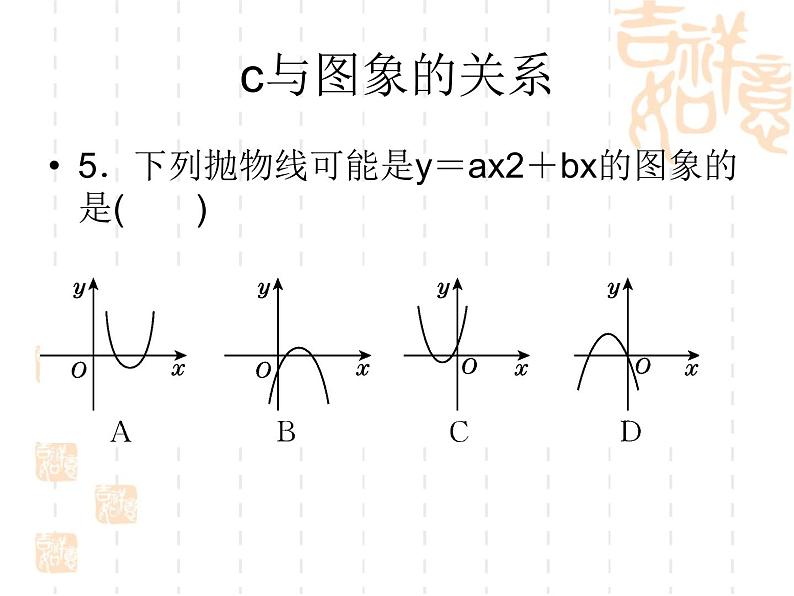
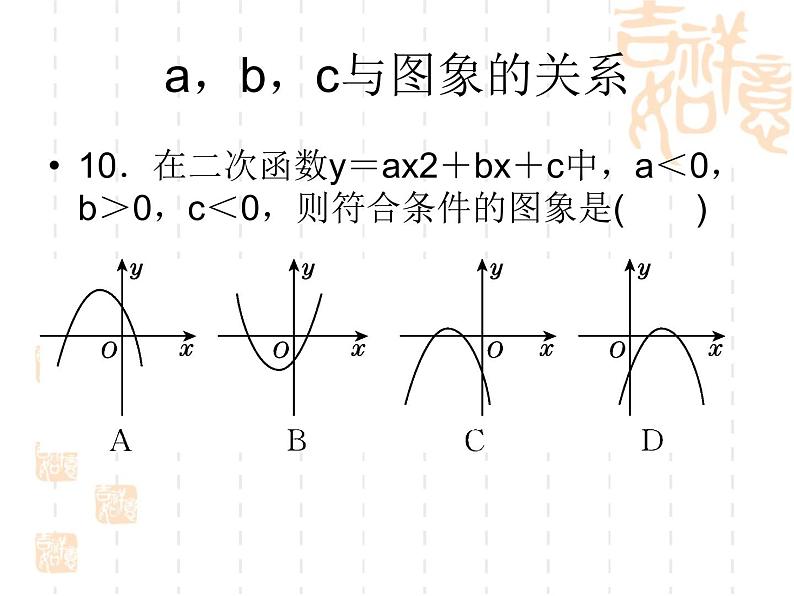
二次函数复习课面对中招4个专项： 1、二次函数的图象与系数的关系 2、求二次函数表达式的常见类型 3、函数中的决策问题 4、二次函数图象信息题的四种常见类型二次函数的图象与系数的关系名师点金：二次函数y＝ax2＋bx＋c(a≠0)的系数a，b，c与图象有着密切的关系：a的取值决定了开口方向和开口大小，a，b的取值影响对称轴的位置，c的取值决定了抛物线与y轴的交点位置，所以a，b，c这三个系数共同决定着抛物线的位置和大小，反之也可以根据二次函数图象情况确定a，b，c的符号或大小．a与图象的关系1．如图所示，四个函数的图象，分别对应的是①y＝ax2；②y＝bx2；③y＝cx2；④y＝dx2，则a，b，c，d的大小关系为(　　)A．a＞b＞c＞d B．a＞b＞d＞cC．b＞a＞c＞d D．b＞a＞d＞c b与图象的关系3．若二次函数y＝3x2＋(b－3)x－4的图象如图所示，则b的值是(　　)A．－5　　　　B．0　　　　C．3　　　　D．44．当抛物线y＝x2－nx＋2的对称轴是y轴时，n______0；当对称轴在y轴左侧时，n______0；当对称轴在y轴右侧时，n______0.(填“＞”“＜”或“＝”)c与图象的关系5．下列抛物线可能是y＝ax2＋bx的图象的是(　　)a，b，c与图象的关系10．在二次函数y＝ax2＋bx＋c中，a＜0，b＞0，c＜0，则符合条件的图象是(　　)求二次函数表达式的常见类型名师点金：求二次函数的表达式是解决二次函数问题的重要保证，在求解二次函数的表达式时一般选用待定系数法，但在具体题目中要根据不同条件，设出恰当的表达式，往往可以给解题过程带来简便．利用一般式求二次函数表达式1．已知一个二次函数的图象经过点A(1，0)，点B(0，6)和点C(4，6)，则这个二次函数的表达式为____________________．2．一个二次函数，当自变量x＝－1时，函数值y＝2；当x＝0时，y＝－1；当x＝1时，y＝－2.那么这个二次函数的表达式为______________．3．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c经过A(－2，－4)，O(0，0)，B(2，0)三点．利用顶点式求二次函数表达式4．已知二次函数y＝ax2＋bx＋c，当x＝1时，有最大值8，其图象的形状、开口方向与抛物线y＝－2x2相同，则这个二次函数的表达式是(　　)A．y＝－2x2－x＋3　　B．y＝－2x2＋4C．y＝－2x2＋4x＋8 D．y＝－2x2＋4x＋65．已知某二次函数的最大值是2，图象顶点在直线y＝x＋1上，并且图象经过点(3，－6)．求这个二次函数的表达式．利用平移法求二次函数表达式．(中考·绥化)把二次函数y＝2x2的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线对应的函数表达式是______________．8．已知y＝x2＋bx＋c的图象向右平移2个单位长度，再向下平移3个单位长度，得到的图象对应的函数表达式为y＝x2－2x－3.(1)b＝__，c＝____；(2)求原函数图象的顶点坐标；(3)求两个图象顶点之间的距离．函数中的决策问题名师点金：函数中的决策问题通常包括两类：一是利用一次函数进行决策，二是利用二次函数进行决策．其解题思路一般是先建立一次函数(二次函数)模型，将实际问题转化为函数问题，然后利用一次函数(二次函数)的图象和性质去分析、解决问题．利用一次函数作决策(中考·临沂)新农村社区改造中，有一部分楼盘要对外销售．某楼盘共23层，销售价格如下：第八层楼房售价为4 000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元．已知该楼盘每套楼房面积均为120米2.若购买者一次性付清所有房款，开发商有两种优惠方案：方案一：降价8%，另外每套楼房赠送a元装修基金；方案二：降价10%，没有其他赠送．(1)请写出售价y(元/米2)与楼层x(1≤x≤23，x取整数)之间的函数关系式；(2)老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更合算．二次函数图象信息题的四种常见类型名师点金：利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言，掌握二次函数的图象和性质，把握二次函数的特点是解决此类问题的关键．利用二次函数的图象比较大小．二次函数y＝－x2＋bx＋c的图象如图，若点A(x1，y1)，B(x2，y2)在此函数图象上，且x1