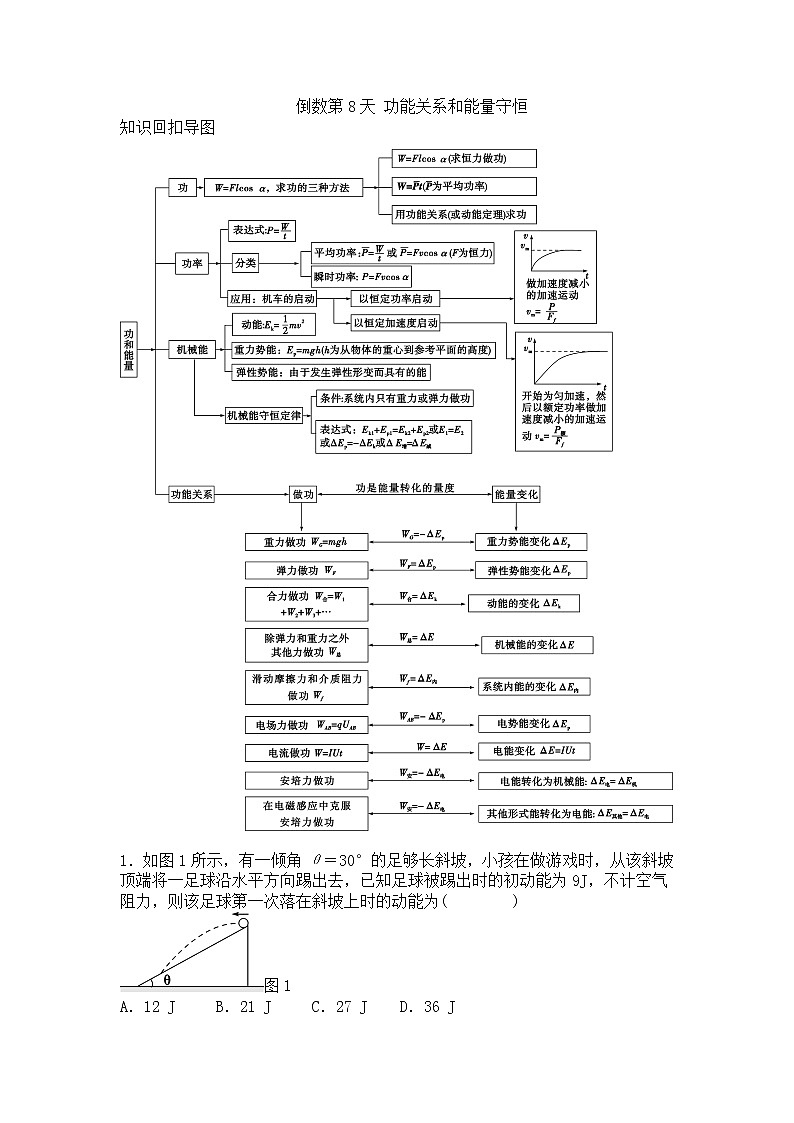
倒数第8天（功能关系和能量守恒）

倒数第8天 功能关系和能量守恒知识回扣导图1．如图1所示，有一倾角θ＝30°的足够长斜坡，小孩在做游戏时，从该斜坡顶端将一足球沿水平方向踢出去，已知足球被踢出时的初动能为9J，不计空气阻力，则该足球第一次落在斜坡上时的动能为(        )图1A．12 J     B．21 J     C．27 J    D．36 J解析足球被踢出后开始做平抛运动，第一次落在斜坡上时对足球的位移进行分解有tan 30°＝＝，得＝，足球第一次落在斜坡上时的动能为m(v＋v)＝21 J，只有选项B正确．答案B2．如图2所示，一质量为1 kg的小球静止在一竖直放置的轻弹簧上，弹簧的劲度系数为k＝50 N/m，现用一竖直向下的F＝10 N的恒力作用在小球上，当小球向下运动到最大速度时撤去F，则小球再回到初始位置时的速度大小为(弹簧形变过程中一直处于弹性限度内)(       )A．2 m/s  B. m/s   C．2 m/s  D. m/s解析小球从初始位置回到初始位置的过程中，重力、弹力做功为零，根据动能定理，WF＝mv2，从开始到最大速度时，小球向下运动的位移Δx＝，则F·Δx＝mv2，F·＝mv2，v＝＝2 m/s，A项正确．3．一条长12 m的传送带，倾角为30°，它能够将工件从地面送到卡车上，每个工件的质量为25 kg，传送带每分钟可传送16个工件，不考虑传送带对工件的加速，g＝10m/s2，下列说法正确的是(       )A．传送带每分钟对工件做的总功是2.4×104JB．摩擦力每分钟对工件做的总功是1.2×104JC．传送带的传送功率为100W  D．传送带的传送功率为200W解析传送工件时不计加速，则工件随传送带一起匀速上升，即摩擦力f＝mgsin  θ，传送带对工件做功实质是传送带的摩擦力f对工件做功，所以W＝nf·l＝16×mgsin 30°×l＝2.4×104 J，A项正确，B项错误；由功率定义，P＝＝W＝400W，知C、D项错误．答案A4．(多选)如图3所示，质量为m的滑块以一定初速度滑上倾角为θ的固定斜面，同时施加一沿斜面向上的恒力F＝mgsin θ.已知滑块与斜面间的动摩擦因数μ＝tanθ，取出发点为参考点，能正确描述滑块运动到最高点过程中产生的热量Q、滑块的动能Ek、机械能E随时间t变化关系及滑块的势能EP随位移x变化关系的是(      )图3解析滑块运动到最高点的过程中，所受的合外力等于沿斜面向下的摩擦力，滑块沿斜面向上做匀减速运动，运动到最高点的过程中产生的热量Q＝fx＝mgsin θ(vt－at2)，图A错误．由动能定理得－mgsin θ(vt－at2)＝Ek－mv2，Ek＝－mgsin θ(vt－at2)＋mv2，图B错误．滑块的重力势能Ep＝mgxsin θ，图C正确．根据题述知，F＝mgsin θ＝μmgcos θ，机械能E随时间t不变，图D正确．答案CD5.如图4所示，一轻绳一端连一小球B，另一端固定在O点，开始时球与O点在同一水平线上，轻绳拉直，在O点正下方距O点L处有一铁钉C，释放小球后，小球绕铁钉C恰好能做完整的竖直面内的圆周运动．图4(1)求绳的长度．(2)求小球第一次运动到最低点时的速度．(3)若让小球自然悬挂，小球恰好与水平面接触于F点，小球质量为m，在水平面上固定有倾角为θ的斜面，斜面高为h，小球与斜面AE及水平面EF间的动摩擦因数均为μ，EF段长为s，让一质量与小球质量相等的滑块从斜面顶端由静止滑下，滑块与小球碰撞后粘在一起，结果两者一起恰好能绕C在竖直面内做圆周运动，则滑块与小球碰撞过程中损失的机械能是多少(不计滑块在E处碰撞的能量损失)?解析(1)设轻绳长为R，则小球绕C在竖直面内做圆周运动时，半径为R－L，恰好能做竖直面内的圆周运动，则在最高点mg＝m根据机械能守恒有mg[R－2(R－L)]＝mv2   解得R＝ L.(2)由机械能守恒定律，小球到最低点时mgR＝mv′2得到v′＝.(3)若滑块与小球粘在一起且恰好能在竖直面内绕C做圆周运动，则碰撞后的共同速度也为v′＝  对滑块根据动能定理有mgh－μmgcos θ－Mgs＝mv  碰撞过程中损失的机械能为E损＝Mv－·2mv′2.解得E损＝mgh－mgL－μmg(hcot θ＋s)．答案　(1) L　(2)  (3)mgh－mgL－μmg(hcot θ＋s)