2021-2022学年辽宁省实验中学等五校协作体高一上学期期末考试数学试题含解析

2021-2022学年辽宁省实验中学等五校协作体高一上学期期末考试

数学试题

一、单选题

1．设集合，，则（       ）

A． B． C． D．

【答案】A

【分析】求函数的定义域求得集合，由此求得.

【详解】由得，所以，

所以.

故选：A

2．命题“，”的否定是（       ）

A．， B．，

C．， D．，

【答案】B

【分析】根据全称量词命题的否定的知识确定正确选项.

【详解】原命题是全称量词命题，其否定是存在量词命题，

注意到是否定结论而不是否定条件，所以B选项正确.

故选：B

3．已知向量，，且，则实数（       ）

A．2 B．1 C． D．

【答案】D

【分析】利用向量共线的坐标表示即可求解.

【详解】∵向量，，且，

∴，解得.

故选：D.

4．已知函数，则的最小值（       ）

A． B． C．0 D．1

【答案】A

【分析】结合函数的单调性确定正确选项.

【详解】对于函数，

任取，，

其中，所以，

所以在上递增.

，

令，

则，

由于在上递增，

当时有最小值为，

所以的最小值为.

故选：A

5．饕餮纹是青铜器上常见的花纹之一，最早见于长江中下游地区的良渚文化陶器和玉器上，盛行于商代至西周早期．将青铜器中的饕餮纹的一部分画到方格纸上，如图所示，每个小方格的边长为一个单位长度，有一点从点出发，每次向右或向下跳一个单位长度，且向右或向下跳是等可能的，那么点经过3次跳动后恰好是沿着饕餮纹的路线到达点的概率为（       ）

A． B． C． D．

【答案】B

【分析】利用古典概型的概率求解.

【详解】解：点从点出发，每次向右或向下跳一个单位长度，跳3次，

则样本空间{（右，右，右），（右，右，下），（右，下，右），（下，右，右），（右，下，下），（下，右，下），（下，下，右），（下，下，下）}，

记“3次跳动后，恰好是沿着饕餮纹的路线到达点B”为事件，则{（下，下，右）}，由古典概型的概率公式可知．

故选：B．

6．已知函数的定义域为，则的定义域为（       ）

A． B．

C． D．

【答案】B

【分析】根据抽象函数定义域的求法求得正确答案.

【详解】依题意函数的定义域为，

，

所以，

解得或，

所以的定义域为.

故选：B

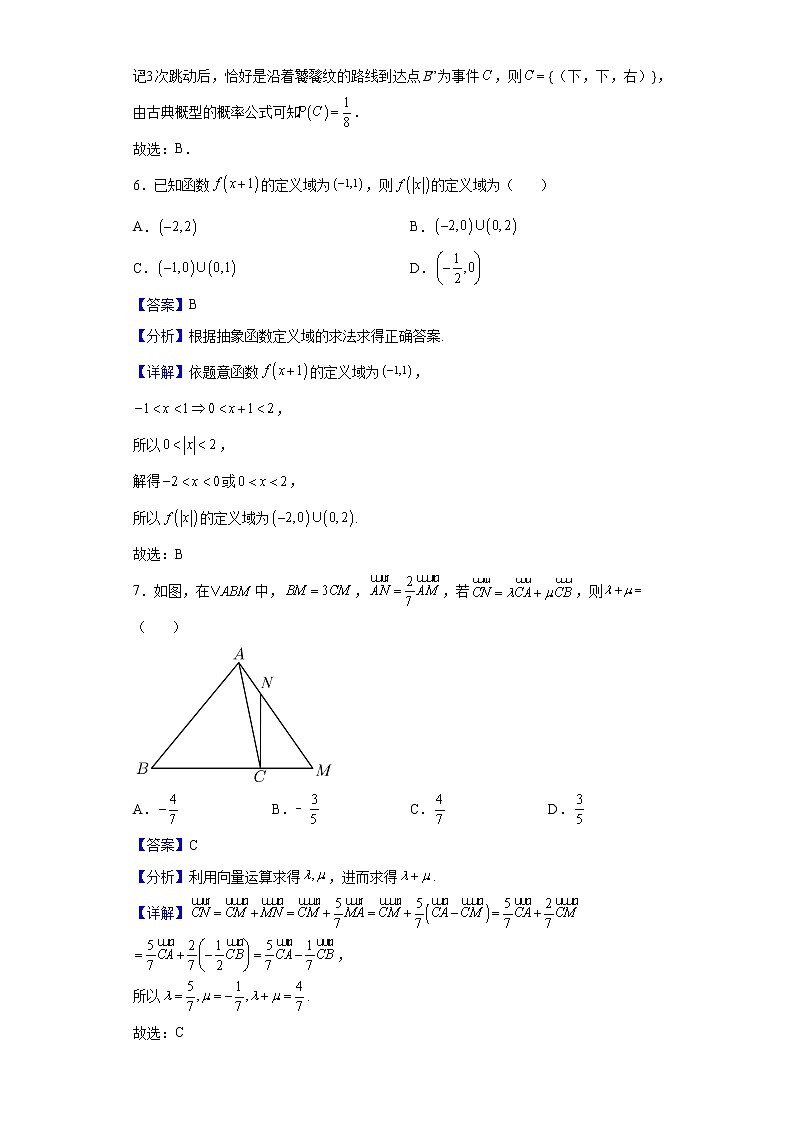
7．如图，在中，，，若，则（       ）

A． B． C． D．

【答案】C

【分析】利用向量运算求得，进而求得.

【详解】

，

所以.

故选：C

8．已知函数，分别是定义在上的奇函数和偶函数，且，若函数有唯一零点，则实数的值为（       ）

A．或 B．1或 C．或 D．或1

【答案】C

【分析】先根据题意求得函数的解析式，再结合函数的对称性得到的方程，解方程，即可求得的值，得到答案.

【详解】由题意，函数，分别是奇函数和偶函数，且，

可得，解得，

则，所以为偶函数，

又由函数关于直线对称，

且函数有唯一零点，可得，即，

即，解得或.

故选：C.

二、多选题

9．某学校为了调查学生一周在生活方面的支出情况，抽出了一个容量为的样本，其频率分布直方图如图所示，其中支出在内的学生有60人，则下列说法正确的是（       ）

A．样本中支出在内的频率为0.03

B．样本中支出不少于40元的人数为132

C．n的值为200

D．若该校有2000名学生，则约有600人支出在内

【答案】BCD

【分析】根据频率之和为补全频率分布直方图，由此对选项进行分析，从而确定正确选项.

【详解】设对应小长方形的高为，

，解得.

所以样本中支出在内的频率为，A选项错误.

，C选项正确.

样本中支出不少于40元的人数为，B选项正确.

该校有2000名学生，则约有人支出在内，D选项正确.

故选：BCD

10．已知函数的图象经过点，则（       ）

A．的图象经过点 B．的图象关于原点对称

C．单调递减区间是 D．在内的值域为

【答案】BD

【分析】由题意得，结合幂函数与反比例函数的图象与性质即可求解.

【详解】将点代入，可得，

则，

因为，故的图象不经过点(2，4)，A错误；

根据反比例函数的图象与性质可得：的图象关于原点对称, 单调递减区间是和，在内的值域为，故BD正确，C错误.

故选：BD.

11．已知函数是上的奇函数和上的增函数，则下列函数中是上的偶函数且在区间上为增函数的有（       ）

A． B． C． D．

【答案】ABC

【分析】根据函数的奇偶性和单调性对选项进行分析，从而确定正确选项.

【详解】依题意函数是上的奇函数和上的增函数，

，则当时，，且递增.

对于A选项，令，的定义域为，

，所以为偶函数，

当时，，所以在上为增函数. A选项正确.

对于B选项，令，的定义域为，

，所以为偶函数，

当时，，所以在上为增函数. B选项正确.

对于C选项，令，的定义域为，

，所以为偶函数，

当时，，

根据复合函数单调性同增异减可知在上为增函数. C选项正确.

对于D选项，令，的定义域为，

，所以D选项错误.

故选：ABC

12．下列关于向量，，的说法正确的是（       ）

A．的充要条件是存在不全为零的实数，使得

B．若且，则

C．若且，则

D．

【答案】ACD

【分析】利用共线向量定理可判断A，利用向量平行的概念可判断B，根据相等向量的定义可判断C，利用向量的加法可判断D.

【详解】对于A，若向量，均为零向量，显然符合题意，且存在不全为零的实数，使得；

若，则由两向量平行可知，存在，即，符合题意，由存在不全为零的实数，使得，根据共线向量定理可得；故A正确；

对于B，当时，若且，则与不一定平行，故B错误；

对于C，根据相等向量的定义可知若且，则，故C正确；

定义D，由向量的加法的几何意义可知，当向量，同向或至少有一个向量为零向量时右端等号成立，当向量，反向或至少有一个向量为零向量时左端等号成立，故D正确.

故选：ACD.

三、填空题

13．计算：_____________

【答案】

【分析】根据根式、指数、对数运算求得正确答案.

【详解】，

，，

，

，

所以

.

故答案为：

14．不等式的解集：_____________.

【答案】.

【分析】化简不等式为，结合分式不等式的解法，即可求解.

【详解】由题意，不等式，可化为，

根据分式不等式的解法，可得或，

即不等式的解集为.

故答案为：.

15．已知函数，，且，则____________（填>，<，≥，≤）.

【答案】

【分析】由进行化简，结合图象判断出的大小关系.

【详解】由得，.

由得，.

画出的图象如下图所示，

由图可知,.

所以，

故答案为：

16．已知函数，函数，若函数有4个零点，则实数的取值范围为_____________.

【答案】

【分析】先判断时，与有个交点.当时，对进行分类讨论，结合与图象交点的个数来求得的取值范围.

【详解】，

函数有4个零点，即与的图象有个交点.

当时，或，

所以当时，与的图象有个交点，

所以只需当时，与的图象有个交点，

下面只研究的情况：

当时，，（舍去）.

当时，，与的图象没有交点.

当时，若，则，此时与的图象有个交点，如下图所示，符合题意.

当时，与的图象没有个交点；

当时，与的图象有个交点，符合题意.

综上所述，的取值范围是.

故答案为：

四、解答题

17．已知甲、乙两组学生某次的测试成绩分数整理成如图所示的茎叶图.

(1)求甲组的平均数，并求乙组的25%分位数；

(2)现在老师想进行试卷分析，在甲组中，，各找一人成绩，组成一组，求79分、97分不全被选中的概率.

【答案】(1)，81；

(2).

【分析】（1）利用平均数的概念及百分位数的概念即得；

（2）利用古典概型概率公式及对立事件概率公式即求.

(1)

由茎叶图的数据可得，

甲组的平均数为，

因为，所以乙组的25%分位数是第3个数81；

(2)

记“79分、97分不全被选中”为事件A，

在甲组中，，各找一人成绩，组成一组，基本事件有种等可能的结果，其中79分、97分全被选中的基本事件有4种，

故，

∴.

18．甲乙两人轮流投篮，每人每次投一球，约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球4次时投篮结束，设甲每次投篮投中的概率为，乙每次投篮投中的概率为，且各次投篮互不影响.

(1)求乙获胜的概率；

(2)投篮结束时，乙只投了3个球的概率.

【答案】(1)

(2)

【分析】（1）利用列举法，结合相互独立事件概率计算公式，计算出所求概率.

（2）利用列举法，结合相互独立事件概率计算公式，计算出所求概率.

(1)

乙获胜包括种情况，计算概率如下：

乙投篮次时获胜：，

乙投篮次时获胜：，

乙投篮次时获胜：，

乙投篮次时获胜：，

所以乙获胜的概率为.

(2)

投篮结束时，乙只投了3个球，包括种情况，计算概率如下：

甲投第球时获胜：，

乙投第球时获胜：，

所以投篮结束时，乙只投了3个球的概率为.

19．已知函数.

(1)若函数在区间内存在零点，求实数的取值范围；

(2)若时，求证：函数在上有且只有一个零点.

【答案】(1)；

(2)详见解析.

【分析】（1）当时，可得，当时，利用二次函数的性质分类讨论即得；

（2）由题可得，利用幂函数及一次函数的性质可知函数为增函数，再利用零点存在定理即证.

(1)

当，即时，由，得，

∴符合题意，

当，即时，函数的对称轴为，

当函数在区间内有两个零点时，则，

解得，

当函数在区间内有一个零点时，或在此区间上单调递增，

∴或，即或且，

当，即时，由得，符合题意；

综上，实数的取值范围为.

(2)

由题可得，又与单调递增，

∴函数在上单调递增，又，

所以有且仅有一个，使，

故函数在上有且只有一个零点.

20．如图，在中，，，AD与BC相交于点M，设，.

(1)试用，表示向量；

(2)在线段AC上取一点E，在线段BD上取一点F，使得EF过点M，设，，求的最小值.

【答案】(1)

(2)

【分析】（1）利用三点共线求得.

（2）先求得的等量关系式，利用基本不等式求得的最小值.

(1)

设，

，

由于三点共线，所以.

所以.

(2)

依题意，，

由于过点，而，，所以，

由（1）得，

所以,

由于三点共线，所以，

，

当且仅当，时等号成立.

21．设为给定的实常数，若函数在其定义域内存在实数使得成立，则称函数为“函数”.

(1)若为“函数”，求实数的值；

(2)已知由（1）中的，且设.若对任意的，当时，都有成立，求实数的最大值.

【答案】(1)

(2)

【分析】（1）根据“函数”的定义求得的值.

（2）通过构造函数，利用所构造函数的减区间来求得的最大值.

(1)

依题意，为“函数”，

即，

即.

(2)

由（1）得，

对任意的，当时，都有成立，

即成立，

不妨设，则，

，

构造函数，则在区间上递减.

，

函数的对称轴为，开口向上.所以在上递增，

函数的对称轴为，开口向下.所以在上递减.

所以的最大值为.

22．已知函数（且），其反函数为.

(1)若函数值域为，求实数的取值范围；

(2)若对任意的，存在，使不等式恒成立，求实数的取值范围；

(3)若时，函数，，探究函数在上是否存在实数，使得，若存在，求出的取值范围，若不存在，请说明理由.

【答案】(1)；

(2)；

(3)答案见解析．

【分析】（1）由题意,解出,则的函数值可以取到所有正实数，从而求出的范围；

（2）不等式成立,根据函数的单调性,即可求出的范围；

（3）当时,求得,通过讨论的范围求其最大值，即可得到M的范围．

(1)

由可得，所以,

若值域为,

则的函数值可以取到所有正实数.

因为的值域为,所以,解得,

所以实数的取值范围是.

(2)

由(1)可知

当时,在上单调递增,故等价于,

故依题意可得对任意的,存在,使不等式恒成立,

则只需,即,解得（舍）.

当时,在上单调递减，故等价于,

故依题意可得对任意的,存在,使不等式恒成立,

则只需,即,则.

综上，实数的取值范围是．

(3)

当时,,则,则,

依题意只需.

令,则．

所以，，

当时，函数在上单调递减，所以，即；

当时, 函数，当且仅当时取等号，所以，即；

当时, 函数在上单调递增，所以，即．

所以，当时,的取值范围是，

当时,的取值范围是,

当时,的取值范围是．