2021-2022学年江西省景德镇市第一中学高一上学期期末数学试题含解析

这是一份2021-2022学年江西省景德镇市第一中学高一上学期期末数学试题含解析，共19页。试卷主要包含了单选题，多选题，填空题，双空题，解答题等内容，欢迎下载使用。
2021-2022学年江西省景德镇市第一中学高一上学期期末
数学试题
一、单选题
1．已知集合，集合，则（       ）
A． B．
C． D．
【答案】C
【分析】先求得集合A、B，再根据交集的运算法则求解即可.
【详解】因为，所以集合，集合或，
所以.
故选：C
2．总体由编号01，02，…，29，30的30个个体组成.利用下面的随机数表选取6个个体，选取方法是从如下随机数表的第1行的第6列和第7列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（       ）
第1行78   16   62   32   08   02   62   42   62   52   53   69   97   28   01   98
第2行32   04   92   34   49   35   82   00   36   23   48   69   69   38   74   81
A．19 B．25 C．26 D．27
【答案】B
【分析】利用随机数表法列举出样本的前个个体的编号，由此可得出结论.
【详解】由随机数表法可知，样本的前个个体的编号分别为、、、、，
因此，选出的第个个体的编号为.
故选：B
3．若函数，当时函数值，则的取值范围是（       ）
A． B．
C． D．
【答案】A
【分析】根据分段函数，分和两种情况，再求解不等式即可得到结果.
【详解】当时，则，所以，即；
当时，则，所以；
综上，.
故选：A.
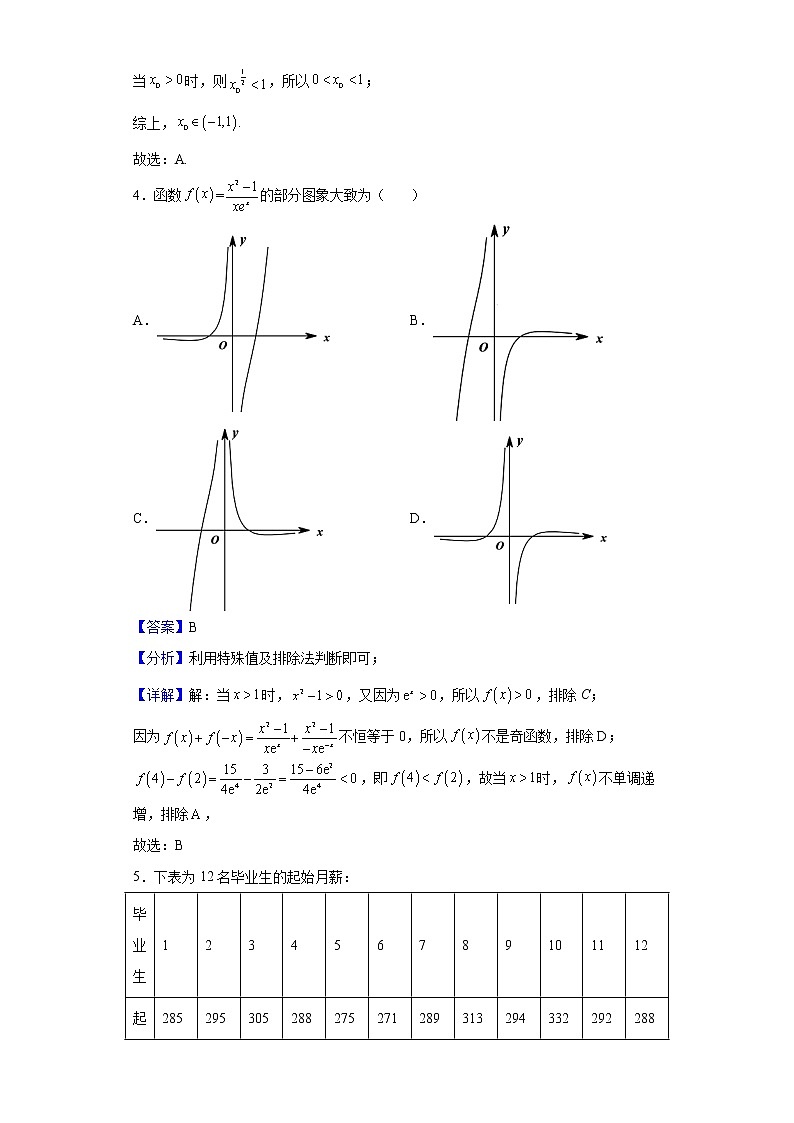
4．函数=的部分图象大致为（       ）
A． B．
C． D．
【答案】B
【分析】利用特殊值及排除法判断即可；
【详解】解：当时，，又因为，所以，排除C；
因为不恒等于0，所以不是奇函数，排除D；，即，故当时，不单调递增，排除，
故选：B
5．下表为12名毕业生的起始月薪：
毕业生
1
2
3
4
5
6
7
8
9
10
11
12
起始月薪
2850
2950
3050
2880
2755
2710
2890
3130
2940
3325
2920
2880

根据表中所给的数据计算75%分位数为（       ）A．2950 B．3050 C．3130 D．3000
【答案】D
【分析】根据百分位数的定义计算即可.
【详解】由小到大排列12个数据为2710，2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325；
因为，
所以75%分位数为，
故选：D
6．已知函数的值域为，那么实数的取值范围是（       ）
A． B．
C． D．
【答案】C
【分析】根据给定条件结合分段函数值域的意义可得在取尽一切负数，再列出不等式求解即可作答.
【详解】函数，而函数是增函数，当时，，则当时，函数值域为，
因函数的值域为，因此，在当时，函数取尽一切负数，
当，即时，，不符合题意，当时，，也不符合题意，当时，为增函数，由可得，
则需，解得，
所以实数的取值范围是：.
故选：C
7．净水机通过分级过滤的方式使自来水逐步达到纯净水的标准，其中第一级过滤一般由孔径为5微米的PP棉滤芯（聚丙烯熔喷滤芯）构成，其结构是多层式，主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质.假设每一层PP棉滤芯可以过滤掉三分之一的大颗粒杂质，过滤前水中大颗粒杂质含量为50mg/L，若要满足过滤后水中大颗粒杂质含量不超过2.5mg/L，则PP棉滤芯层数最少为（       ）（参考数据：，）
A．5 B．6 C．7 D．8
【答案】D
【分析】由题意得，经层滤芯过滤后水中大颗粒杂质含量为，则，两边取对数化简求解即可得答案.
【详解】由题意得，经层滤芯过滤后水中大颗粒杂质含量为，
则，得，
所以，
，
所以，，
得，
因为为正整数，
所以的最小值为8，
故选：D
8．已知函数，，对于任意，存在有，则实数的取值范围是（       ）
A． B．
C． D．
【答案】B
【分析】使，据此求解即可.
【详解】对于任意，存在有等价于.
由，函数单调递增，可得
，，对称轴为，
时，，
，
解得.
故选：B
二、多选题
9．从装有大小和形状完全相同的2个红球和3个黑球的口袋内任取2个球，下列各对事件中，互斥而不对立的是
A．“至少一个红球”和“都是红球”
B．“恰有一个红球”和“都是红球”
C．“恰有一个红球”和“都是黑球”
D．“至少一个红球”和“都是黑球”
【答案】BC
【分析】利用对立事件、互斥事件的定义直接求解．
【详解】解：从装有大小和形状完全相同的2个红球和3个黑球的口袋内任取2个球，
在中，“至少一个红球”和“都是红球”能同时发生，不是互斥事件，故错误；
在中，“恰有一个红球”和“都是红球”不能同时发生，是互斥而不对立事件，故正确；
在中，“恰有一个红球”和“都是黑球”不能同时发生，是互斥而不对立事件，故正确；
在中，“至少一个红球”和“都是黑球”是对立事件，故错误．
故选：．
【点睛】本题考查命题真假的判断，考查对立事件、互斥事件的定义等基础知识，考查运算求解能力，属于基础题．
10．某地在2020年采用旧高考模式（即分文科和理科，理科必选物理，文科不选物理），在2021年实行了新高考改革，采用新高考模式（即“3＋1＋2”模式，“1”指物理和历史必选其一）．图1是某地2020年高考理科学生总分分布扇形图，图2是某地2021年高考物理类学生（选择物理的学生）总分分布条形图．由于新高考改革，该地2021年选择物理的学生人数较2020年理科学生人数下降了13%，则下列说法正确的有（       ）

A．该地2020年高考理科学生总分在350分至450分段的学生人数占30%
B．该地2021年高考物理类学生总分在550分至650分段的学生人数是2020年高考理科学生总分同分段学生人数的2倍
C．该地2020年高考理科学生总分和2021年高考物理类学生总分的中位数均在450分至550分段
D．相比2020年高考理科学生总分不低于450分的人数，新高考模式下高考物理类学生总分不低于450分的人数占比增加
【答案】ACD
【分析】对A，由频率之和为1可计算总分在350分至450分段的学生人数比例；对B，通过对分数段在内的人数比例计算可判断错误；通过频率累计和可判断C、D项正确.
【详解】对A，2020年高考理科学生总分在350分至450分的学生人数占比为，故A项正确；
对B，由于2021年选择物理的学生人数较2020年理科学生人数下降了13%，假设2020年理科学生人数为单位1，则分数在内的人数为，2021年选择物理且分数在内的人数为，，故2021年高考物理类学生总分在550分至650分段的学生人数小于2020年高考理科学生总分同分段学生人数的2倍，故B项错误；
对C，2020年高考理科学生总分小于450分的人数占比为，小于550分的人数占比为，故中位数应该在450分至550分段．
同理，2021年高考物理类学生总分分数小于450分的人数占比为，小于550分的人数占比为，故中位数应该在450分至550分段，C项正确；
对D，2020年高考理科学生总分不低于450分的人数占，2021年高考物理类学生总分不低于450分的人数占．故高考物理类学生总分不低于450分的人数占比增加，故D项正确.
故选：ACD
11．给出下列四个结论，其中所有正确结论的序号是（       ）
A．若，，，则
B．函数在上只有一个零点，且该零点在区间上.
C．实数是命题“，”为假命题的充分不必要条件
D．定义在上的函数满足，且，，则不等式的解集为
【答案】ACD
【分析】利用对数函数的单调性判断A，根据零点存在性定理及函数单调性判断B，根据二次不等式的求解及充分必要条件判断C，构造函数，根据函数单调性解不等式判断D.
【详解】对于A，若，则，，
所以，故A正确；
对于B，函数在上单调递增，且，故该零点在区间上错误，故B错误；
对于C，命题“，”为假命题，则“，”为真命题，当时，，为真命题，当时，，为假命题，当时，若时，，这时“，”为真命题，当时，，这时“，”为假命题，综上实数是命题“，”为假命题的充分不必要条件，故C正确；
对于D，定义在上的函数满足，不妨设
，则，即，令，
则，故单调递减，因为，所以，由变形为，即，根据单调递减，所以，故D选项正确.
故选：ACD
12．设函数，集合，则下列命题正确的是（       ）
A．当时，
B．当时
C．若集合M有三个元素，则k的取值范围为
D．若（其中），则
【答案】ABD
【分析】解一元二次方程直接求解集即可判断A，由题设易知集合中方程无解即可判断B，画出的图象，令根据二次函数的性质及所得的图象判断CD正误即可.
【详解】A：时，或，结合解析式：时有或，时有，所以，正确；
B：时，由，知方程无解，则，正确；
由解析式可得其函数图象如下图示：

令，开口向上且对称轴为，
若，则，即，有以下情况：
1、，：
此时，令，则在上有一个零点，
∴，可得，
2、，，由A知：.
综上：，故C错误；
若，由函数的性质及图象知：必有，.
此时，，，
所以，，所以，故D正确.
故选：ABD
【点睛】关键点点睛：C、D选项中，画出大致图象，结合二次函数的性质判断给定集合对应的的可能取值，再结合图象判断正误.
三、填空题
13．化简____________.
【答案】214
【分析】根据指数幂的运算法则计算即可.
【详解】原式＝＋2－3－2＋1＝214.
故答案为：214.
14．我国古代的一些数字诗精巧有趣，又饱含生活的哲学，如清代郑板桥的《题画竹》》：“一两三枝竹竿，四五六片竹叶，自然淡淡疏疏，何必重重叠叠.”现从1，2，3，4，5，6中随机选取2个不同的数字组成，则恰好能使得的概率是____________.
【答案】0.6
【分析】列举基本事件，直接求概率即可.
【详解】随机选取2个不同的数字组成,共有
而，，3，4，5，6，
，，2，4，5，6，
，，2，3，5，6，
，，2，3，4，6，
，，2，3，4，5，共有25种，
其中
1，2，3，4，5，6这6个数字中满足的数对有：
，，4，5；
，；
，；
，；

共15种，
所求概率为．
故答案为：．
15．若函数的定义域为，且满足如下两个条件：①在内是单调递增函数；②存在，使得在上的值域为那么就称函数为“希望函数”，若函数是“希望函数”，则实数的取值范围为___________.
【答案】
【分析】根据“希望函数”的概念，利用对数函数的性质和二次函数的性质即解．
【详解】∵函数是“希望函数”，
∴，即有两个解，
∴m，n是方程的两个不等的实根，
设，则，
∴方程等价为的有两个不等的正实根，
即，
∴，解得，
故答案为：.
四、双空题
16．甲、乙两支田径队的体检结果为：甲队体重的平均数为60kg，方差为200，乙队体重的平均数为70kg，方差为250，又已知甲、乙两队的队员人数之比为1:4，那么甲、乙两队全部队员的平均体重为_____________；甲、乙两队全部队员的方差为______________
【答案】     68kg     256
【分析】直接根据平均数和方差公式进行计算，即可得到答案；
【详解】由题意可知，甲队队员在所有队员中所占权重为，
，乙队队员在所有队员中所占权重为，
则甲、乙两队全部队员的平均体重为，
甲、乙两队全部队员的体重方差为.
故答案为：68kg；256.
五、解答题
17．已知，其中为奇函数，为偶函数.
(1)求与的解析式；
(2)解关于不等式.
【答案】(1)，
(2)
【分析】（1）运用函数的奇偶性的定义，将换为，联立方程，解方程可得所求解析式；
（2）先判断函数的定义域及单调性，再由奇偶性化简不等式后由单调性求解.
(1)
由于函数为奇函数，为偶函数，
可得，，
因为，
所以，
即，
解得，．
(2)
的定义域为，且，
由复合函数的单调性可知在上单调递减．
因为为奇函数，
故由可得，
又在上单调递减，
所以，解得，
所以不等式的解集为.
18．第32届夏季奥林匹克运动会于2021年7月23日至8月8日在日本东京举办，某国男子乒乓球队为备战本届奥运会，在某训练基地进行封闭式训练.甲、乙两位队员进行对抗赛，每局依次轮流发球，连续赢2个球者获胜.通过分析甲、乙过去对抗赛的数据知，甲发球甲赢的概率为，乙发球乙赢的概率为，不同球的结果互不影响，已知某局甲先发球.
(1)求该局打4个球乙赢的概率；
(2)求该局打5个球结束的概率.
【答案】(1)
(2)
【分析】(1)先设乙发球乙赢为事件A，甲发球乙赢为事件，然后分析这4个球的发球者及输赢者，即可得到所求事件的构成，利用相互独立事件的概率计算公式即可求解；
(2)先将所求事件分成乙赢与甲赢这两个互斥事件，再分析各事件的构成，利用互斥事件和相互独立事件的概率计算公式即可求得概率.
(1)
设乙发球乙赢为事件A，甲发球乙赢为事件，该局打4个球乙赢为事件，
由题知，，
，
该局打4个球乙赢的概率为.
(2)
设该局打5个球结束时甲贏为事件，乙贏为事件，打5个球结束为事件，
易知为互斥事件，D＝，E＝，F＝，
=，
=，
，
该局打5个球结束的概率为.
19．2021年3月18日，位于孝感市孝南区长兴工业园内的湖北福益康医疗科技有限公司正式落地投产，这是孝感市第一家获批的具有省级医疗器械生产许可证资质的企业，也是我市首家“一次性使用医用口罩、医用外科口罩”生产企业.在暑期新冠肺炎疫情反弹期间，该公司加班加点生产口罩、防护服，消毒水等防疫物品，保障抗疫一线医疗物资供应，在社会上赢得一片赞誉.在加大生产的同时，该公司狠抓质量管理，不定时抽查口罩质量，该企业质检人员从所生产的口罩中随机抽取了100个，将其质量指标值分成以下六组：，，，…，，得到如下频率分布直方图.

(1)求出直方图中的值；
(2)利用样本估计总体的思想，估计该企业所生产的口罩的质量指标值的平均数和中位数（同一组中的数据用该组区间中点值作代表，中位数精确到0.01）；
(3)现规定：质量指标值小于70的口罩为二等品，质量指标值不小于70的口罩为一等品.先用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩，再从抽出的5个口罩中一次性抽取2个口罩，求有二等品的概率.
【答案】(1)0.030
(2)平均数为71，中位数为73.33
(3)
【分析】（1）通过频率分布直方图面积的和为1，求解m即可；
（2）根据概念求出平均数，设中位数为n，然后求解n即可；
（3）所抽取的5个口罩中一等品，二等品各有3个，2个，利用古典概型概率公式求解即可.
(1)
由，得
(2)
平均数，
设中位数为n，
则，得．
故可以估计该企业所生产口罩的质量指标值的平均数为71，中位数为73.33．
(3)
由频率分布直方图可知，100个口罩中一等品，二等品各有60个，40个，
由分层抽样可知，所抽取的5个口罩中一等品，二等品各有3个，2个．
记这3个一等品为a，b，c，2个二等品为d，e，则从5个口罩中抽取2个的可能结果有：（a，b），（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d），（c，e），（d，e），共10种，
其中有二等品的可能结果有：（a，d），（a，e），（b，d），（b，e），（c，d），（c，e），（d，e），共7种．
故有二等品的概率为.
20．2009年某市某地段商业用地价格为每亩48万元，由于土地价格持续上涨，到2021年已经上涨到每亩96万元.现给出两种地价增长方式，其中：是按直线上升的地价，：是按对数增长的地价，是2009年以来经过的年数，2009年对应的值为0.
(1)求，的解析式；
(2)2021年开始，国家出台“稳定土地价格”的相关调控政策，为此，该市要求2025年的地价相对于2021年上涨幅度控制在10%以内，请分析比较以上两种增长方式，确定出最合适的一种模型.（参考数据：）
【答案】(1)，,，;
(2)应选择模型，理由见解析.
【分析】（1）由，， ，分别代入解析式求解即可得解；
（2）分别由,计算，，分别算出增长率与10%比较即可.
(1)
由题知：，，代入解析式，
所以，解得：，
所以，；
又，，代入解析式可得
，
解得：，
所以，；
(2)
若按照模型，到2025年时，，，
直线上升的增长率为，不符合要求；
若按照模型，到2025年时，，
，
对数增长的增长率为，符合要求；
综上分析，应该选择模型．
21．在①函数满足，函数的图象与直线只有一个交点；②函数过点，且不等式的解集为，这两个条件中选择一个补充在下面问题中，并解答：
已知二次函数，且_____________________.
(1)求的解析式；
(2)若方程有且仅有一个实根，求实数m的取值范围.
注：如果选择多个条件分别解答，按第一个解答计分.
【答案】(1);
(2)或.
【分析】（1），选①，根据条件建立方程求出，再由函数的最值求出，可得的解析式；选②由不等式的解可知方程的根，由根与系数的关系建立方程，再由函数过点建立方程求解即可得出的解析式；
（2）令，换元后转化为方程有且仅有一个正根，分类讨论求解即可.
(1)
，
选①，
，

解得，，

由函数的图象与直线只有一个交点知，
解得，
故；
选②，
由的解集为知，0,2为方程的两根，
所以，
即，
，
又函数过点，
，解得，
故.
(2)
令，
则由方程可得，
所以方程有且仅有一个实根可转化为方程有且仅有一个正根，
当时，，舍去，不满足题意，
当时，由图象开口向上的抛物线，且恒过，
所以方程恒有一正根满足题意，
当时，若方程有且仅有一个正根，
则需满足，解得，
综上，实数m的取值范围为或.
22．对于函数，，，如果存在实数，使得，那么称为，的生成函数.
(1)设，，，，生成函数.若不等式在上有解，求实数的取值范围.
(2)设函数，，是否能够生成一个函数，且同时满足：①是偶函数；②在区间上的最小值为，若能够生成，则求函数的解析式，否则说明理由.
【答案】(1)；
(2)存在，，理由见解析.
【分析】（1）根据题意新定义得到的解析式，然后将问题转化为在上有解，利用换元法转化为二次函数求解最值即可；
（2）利用待定系数法设，根据，得到对任意恒成立，从而得到，再利用换元法以及对勾函数进行分析求解，即可得到答案．
(1)
由题意可得，， ，，，
所以，
不等式在上有解，
等价于在上有解，
令，则，
由在上单调递减，
所以当时，取得最大值，故．
即
(2)
设，则．
由，得，
整理得，即，即对任意恒成立，
所以．
所以
．
设，
令，则，
由对勾函数的性质可知在单调递减，上单调递增，
∴在单调递增，
∴，且当时取到“”．
∴，
又在区间的最小值为，
∴，且，此时，．
所以．
【点睛】关键点点睛：考查新定义函数问题，实质上还是对函数性质、恒成立、存在性问题、求值域等问题的考查，关键点是能够正确读懂题意，理解其本质.