四川省大数据精准教学联盟2021-2022学年高三下学期第二次统一监测数学(理)试题
展开四川省大数据精准教学联盟2021-2022学年高三下学期第二次统一监测数学(理)试题
第I卷(选择题)
| 一、单选题 |
1.设集合,,则( )
A. B.
C. D.
2.已知,则( )
A. B. C. D.
3.已知命题,那么为( )
A. B. C. D.
4.已知二项式的展开式中,项的系数为40,则( )
A.2 B.-2 C.2或-2 D.4
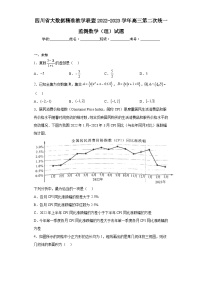
5.《算法统宗》是由明代数学家程大位所著的一部以用数学著作,该书清初传入朝鲜、东南亚和欧洲,成为东方古代数学的名著.书中卷八有这样一个问题:“今有物一面平堆,底脚阔七个,上阔三个,问共若干?”如图所示的程序框图给出了解决该题的一个算法,执行该程序框图,输出的S即为总个数,则总个数( )
A.18 B.25 C.33 D.42
6.已知是两个不同的平面,l,m是两条不同的直线,有如下四个命题:
①若,则;②若,则;
③若,则﹔④若,则.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
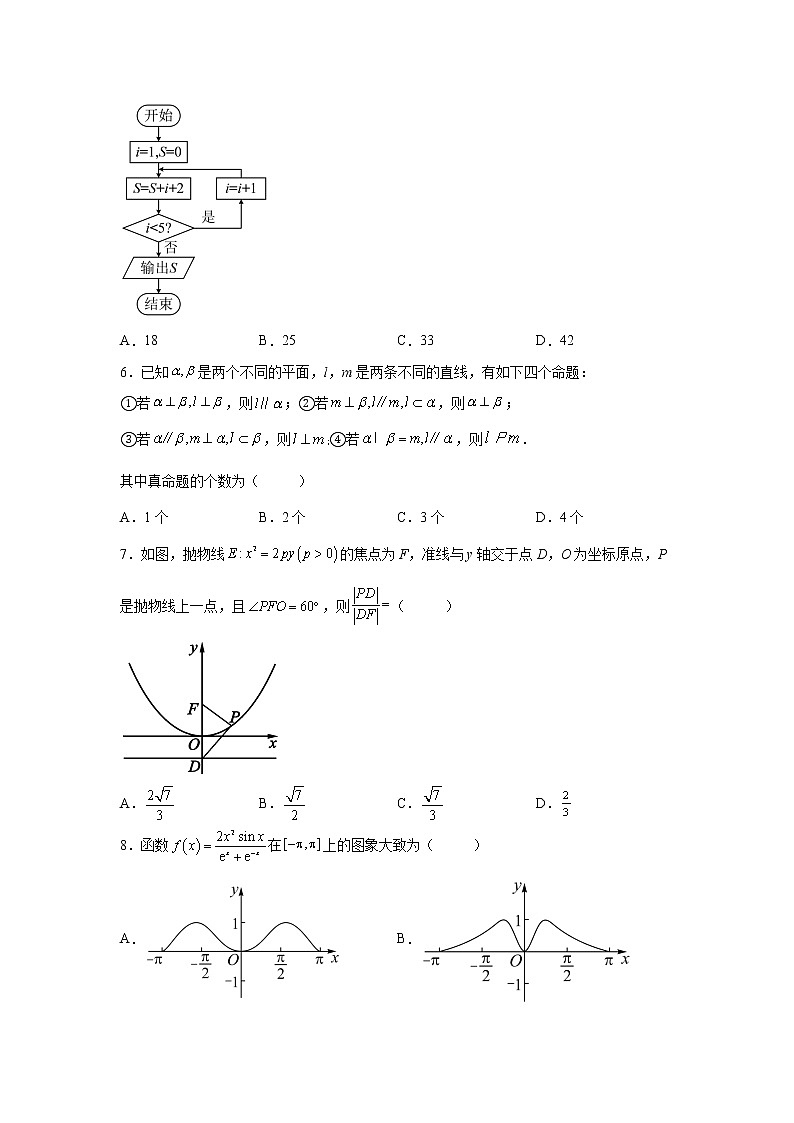
7.如图,抛物线的焦点为F,准线与y轴交于点D,O为坐标原点,P是抛物线上一点,且,则( )
A. B. C. D.
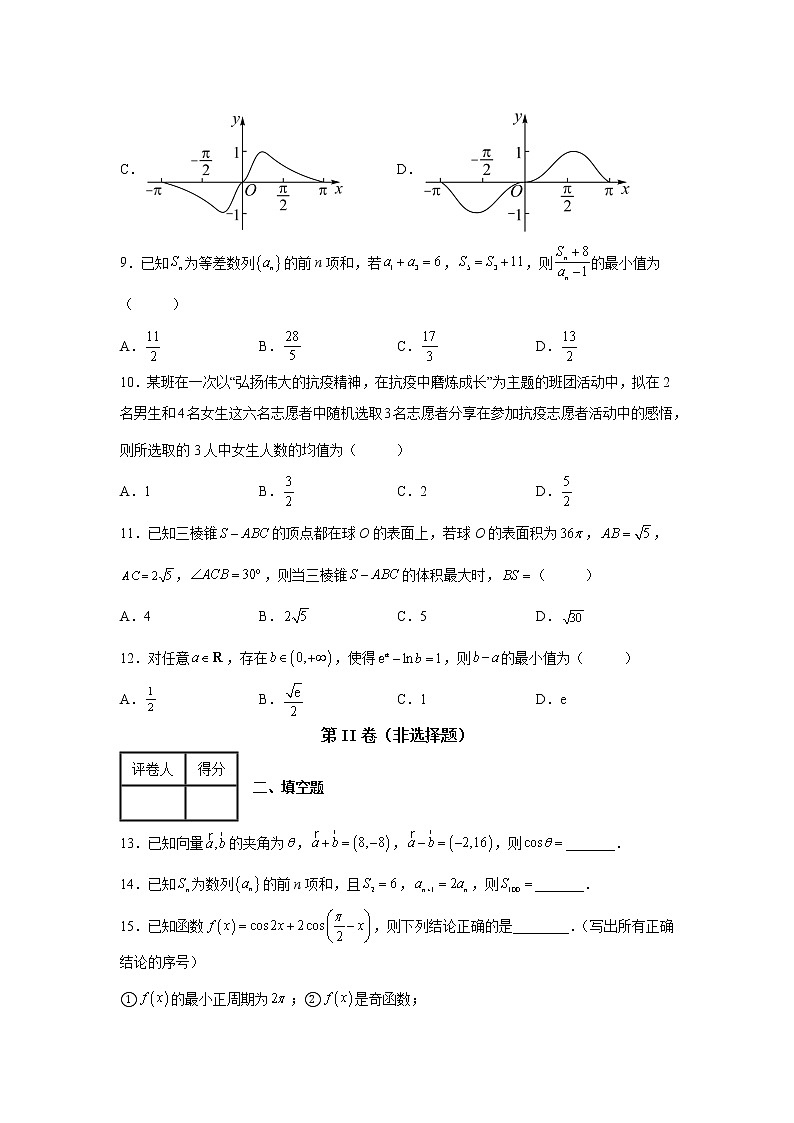
8.函数在上的图象大致为( )
A. B.
C. D.
9.已知为等差数列的前n项和,若,,则的最小值为( )
A. B. C. D.
10.某班在一次以“弘扬伟大的抗疫精神,在抗疫中磨炼成长”为主题的班团活动中,拟在2名男生和4名女生这六名志愿者中随机选取3名志愿者分享在参加抗疫志愿者活动中的感悟,则所选取的3人中女生人数的均值为( )
A.1 B. C.2 D.
11.已知三棱锥的顶点都在球O的表面上,若球O的表面积为,,,,则当三棱锥的体积最大时,( )
A.4 B. C.5 D.
12.对任意,存在,使得,则的最小值为( )
A. B. C.1 D.e
第II卷(非选择题)
| 二、填空题 |
13.已知向量的夹角为,,,则_______.
14.已知为数列的前n项和,且,,则_______.
15.已知函数,则下列结论正确的是________.(写出所有正确结论的序号)
①的最小正周期为;②是奇函数;
③的值域为;④在上单调递增.
16.设双曲线的左,右焦点分别为,,左,右顶点分别为A,B,以AB为直径的圆与双曲线的渐近线在第一象限的交点为P,若为等腰三角形,则直线的倾斜角的大小为________.
| 三、解答题 |
17.为了解某地区经济发展情况,现对2012年~2021年该地区生产总值y(单位:百亿元)进行了统计,制成如下散点图,其中年份代码x的值1~10分别对应2012年至2021年.
(1)建立y关于x的线性回归方程(系数精确到0.01);
(2)若2021年该地区生产总值为2150亿元,在此基础上根据(1)中的模型预测,2022年该地区生产总值能否实现的增长目标?
参考数据:,,,
参考公式:对于一组数据,回归方程中的斜率和截距的最小二乘估计公式分别为.
18.在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,判断的形状;若问题中的三角形不存在,说明理由.
问题:是否存在,它的内角A,B,C的对边分别为a,b,c,且a,b,c成等差数列,﹐__________?
注:如果选择多个条件分别解答,按第一个解答计分.
19.如图,在直棱柱中,点E,F分别为,BC的中点,点G是线段AF上的动点.
(1)确定点G的位置,使得平面平面,并给予证明;
(2)在第(1)题的条件下,若,,求二面角的余弦值.
20.在直角坐标系xOy中,长为3的线段AB的两端点A,B分别在x,y轴上滑动,动点M满足
(1)求动点M的轨迹E的方程;
(2)设过点的动直线l与(1)中的轨迹E交于C,D两点,是否存在定实数t,使得为定值?若存在,求出t的值;若不存在,请说明理由.
21.已知函数.
(1)若时,过点作曲线的切线l,求l的方程;
(2)若函数在处取极小值,求a的取值范围.
22.在直角坐标系中,曲线C的参数方程为(为参数),以坐标原点O为极点,x轴的非负半箱为极轴建立极坐标系,点M的极坐标为,直线l的极坐标方程为.
(1)求点M的直角坐标和直线l的直角坐标方程;
(2)若N为曲线C上的动点,求的中点P到直线l的距离的最小值及此时点P的极坐标.
23.己知.求证:
(1);
(2).
参考答案:
1.B
【解析】
【分析】
先求出,然后可得答案.
【详解】
由题得,则.
故选:B
2.D
【解析】
【分析】
根据复数的除法运算可得答案.
【详解】
由已知得,所以.
故选:D
3.A
【解析】
【分析】
根据存在量词命题的否定为全称量词命题即得.
【详解】
由已知命题,则是.
故选:A.
4.C
【解析】
【分析】
根据二项展开式的通项公式,令的指数为4可求得,再根据系数为40求解即可
【详解】
由,令,解得,所以项的系数为,解得.
故选:C
5.B
【解析】
【分析】
按照程序框图的流程图进行计算,得到答案.
【详解】
输出
故选:B
6.B
【解析】
【分析】
①利用直线与平面的位置关系判断;②利用线面垂直的性质定理和面面垂直的判定定理判断;③利用面面平行的性质定理和线面垂直的定义判断;④利用直线与直线的位置关系判断.
【详解】
①,若,则或,故错误;
②若,则,又,则,故正确;
③若,则,又,则,故正确;
④若,则或l与m异面,故错误;
故选:B
7.C
【解析】
【分析】
分别过作轴与准线的垂线,再根据结合抛物线的性质计算即可
【详解】
如图,过P作PH垂直轴于H,过P作PB垂直准线于B,设,则因为,结合抛物线的基本性质有,,.所以
故选:C
8.D
【解析】
【分析】
由可得为奇函数,排除A,B;当时,,代入特殊值即可判断结果.
【详解】
由知为奇函数,排除A,B,
当时,因为,则,所以排除C,
故选:D.
9.A
【解析】
【分析】
根据条件求出,然后利用基本不等式求解即可.
【详解】
设的公差d,由有,
解得,所以,
则,当且仅当时等号成立.
故选:A
10.C
【解析】
【分析】
记所选取的3人中女生人数为X,则X的可能值为1,2,3,求出取每个值的概率后,根据均值公式计算可得结果.
【详解】
记所选取的3人中女生人数为X,则X的可能值为1,2,3,
则,
,
则X均值.
故选:C.
11.D
【解析】
【分析】
设是的外心,即可得到,再根据球的表面积求出球的半径,即可得,当且仅当、、三点共线且平面和点位于点异侧时,三棱锥的体积最大,再由勾股定理计算可得.
【详解】
在中,根据正弦定理,可得,所以.如图,
设为的外心,则为AC的中点,且,由于球O的表面积为,所以球O的半径,
当,,三点共线且平面CAB和点S位于点O的异侧时,
三棱锥的体积最大.此时
故选:D
12.C
【解析】
【分析】
令,把用表示,然后引入新函数,利用导数求得函数的最小值即得.
【详解】
由题,令,则所以,令
,则,令,
则,则即在时单调递增,
又,则时时,
所以时取得极小值也即为最小值,最小值,即的最小值为1.
故选:C.
13.
【解析】
【分析】
根据条件求出的坐标,然后可算出答案.
【详解】
由已知可得,
所以
故答案为:
14.
【解析】
【分析】
由条件可得数列是以2为首项,2为公比的等比数列,然后可算出答案.
【详解】
由得,且,解得,
所以数列是以2为首项,2为公比的等比数列,所以.
故答案为:
15.①③④
【解析】
【分析】
先对函数解析式化简,再对①②③④一一判断:
对于①:利用周期性的定义进行判断;
对于②:取特殊值:由,否定结论;
对于③:直接求出的值域,即可判断;
对于④:利用复合函数单调性法则进行判断.
【详解】
由,定义域为R.
对于①:因为的最小正周期为,即恒成立,
所以,
所以的最小正周期为.故①正确;
对于②:取特殊值:,而,所以,故不是奇函数.故②错误;
对于③:令,则.所以在单增,在单减,所以,即的值域为.故③正确;
对于④:令,则在上单调递增,且.
而在上单调递增,所以在上单调递增.故④正确.
所以命题②不正确,命题①③④正确.
故答案为:①③④.
16.##
【解析】
【分析】
由题意求得点P的坐标,再根据为等腰三角形,得到,从而得到a,b,c的关系,再利用斜率公式求解.
【详解】
解:以AB为直径的圆的方程为,
双曲线过第一象限的渐近线方程为.
由,得.
由为等腰三角形,得点P在线段的中垂线上,即.
由,得,
即,得,
所以.而,
则,
故直线倾斜角为,
故答案为:.
17.(1);
(2)2022年该地区生产总值能实现5%的增长目标.
【解析】
【分析】
(1)利用最小二乘法即得;
(2)利用线性回归方程可得2022年该地区生产总值的估计值,进而可得增长率估计值,即得.
(1)
由题可得,
设线性回归方程,
则,
,
所以,y关于x的线性回归方程;
(2)
由,
2022年该地区生产总值的估计值为(百亿元),
由题,2021年该地区生产总值为21.5 百亿元,
根据该回归模型,增长率估计值为 ,
所以,2022年该地区生产总值能实现5%的增长目标.
18.答案见详解.
【解析】
【分析】
若选①由面积公式先求得,根据基本不等式求得,从而求得,故不存在;若选②利用余弦定理和面积公式结合角的范围即可求出角,从而求解各边长,即可判断的形状;若选③利用面积公式先求解角,再用余弦定理求解各边长,即可判断的形状.
【详解】
若选①,这样的不存在.理由如下:
由已知得,所以,
则.又,所以.
又由
所以与正弦函数的有界性矛盾.
故这样的不存在.
若选②,这样的存在.
由,得,
由余弦定理得,
所以.(1)
又,即,(2)
由(1),(2)消去ac得,
所以,即,
因为a,b,c成等差数列,b不是最大边,所以
所以,即.则,解得,
此时为等边三角形.
若选③,这样的存在.
由题意有,
则,所以,
因为a,b,c成等差数列,b不是最大边,所以
所以,
由余弦定理得
解得,所以,又,解得.此时为等边三角形.
19.(1)点G为的重心;证明见解析
(2)0
【解析】
【分析】
(1)取AB中点D,连结CD交AF于G,分别由四边形和四边形是平行四边形,得到,.再利用面面平行的判定定理证明;
(2)以C为坐标原点建立空间直角坐标系,分别求得平面的一个法向量和平面的一个法向量,然后由求解.
(1)
证明:如图所示:
取AB中点D,连结CD交AF于G,即G为的重心(或G为线段AF靠近F的三等分点等)时,平面平面.
证明:连结DE.
因为在三棱柱中,D,E分别为AB,的中点,
所以,且,则四边形是平行四边形,
故.
又平面,平面
所以平面.
因为在三棱柱中,D,E分别是AB,的中点,
则且,四边形是平行四边形,
所以.又平面,平面,
所以平面.
又平面,平面,,
所以平面平面.
(2)
以C为坐标原点建立如图所示空间直角坐标系,
则.
设,由(1)知,,即.
解得,即.
所以.
设平面的一个法向量,
由,得.
令,则,即.
设平面的一个法向量,
由,得.
令,则,即.
设二面角的平面角为,
则,
所以二面角的余弦值为0.
20.(1)
(2)存在;
【解析】
【分析】
(1)设,由向量的数乘运算,用表示出,由可得轨迹方程;
(2)假设存在满足题意的直线,设.当直线l的斜率存在时,设其方程为.代入椭圆方程,应用韦达定理得,计算并代入,分析它是与无关的常数,由此得出值,再检验这个值对斜率不存在的直线也适用,由此得结论.
(1)
设
由,得,即
而,即.所以,即.
(2)
假设存在满足题意的直线,设.
当直线l的斜率存在时,设其方程为.
由,消去y,得.
则.
所以,,
则
当且仅当,即时,
当直线l的斜率不存在时,,若
则.
综上,存在实数,使得为定值为5.
21.(1);
(2).
【解析】
【分析】
(1)求出导函数,然后设切点的坐标为,然后得到斜率并写出切线方程,再将点(0,0)代入切线方程解出,最后得到切线方程;
(2)先求出导函数,且发现,然后设并求出导函数,进而分,,和四种情况进行讨论得到的单调性,进一步得到的单调性,讨论出函数在处的极值,最后得到答案.
(1)
时,.
设切点,则,
故切线l的方程为,
由于切线l过点,则,
即,解得,故切线方程为.
(2)
,,
令,则,
①当时,可知,在上单调递增,又,
则时,即,单调递减,时,即,单调递增
故在时取得极小值,故满足条件.
②当时,则在上为增函数,又,
若,,当 时,即单调递减,当 时,即单调递增,而,于是,即函数在上单调递增,不合题意;
若,,而,则存在使得,且时,则即单调递减,又,故时,单调递增,时,单调递减,此时为的极大值点,不合题意.
若,则,限定,故,于是当且时,,那么存在,使得.
所以时,,在上单调递增,而,于是,时,即,单调递减,时,即,单调递增,此时为的极小值点,符合题意.
综上所述:函数在处取极小值时a的取值范围是.
【点睛】
本题难度较大,首先需要对函数进行二次求导,紧紧抓住“导函数的正负确定原函数的增减”;其次,“时”这一步函数的放缩有一定的技巧性,平常注意归纳总结.
22.(1)点M的直角坐标为,直线l的直角坐标方程为;
(2)的中点P到直线l的距离的最小值为,此时点P的极坐标为.
【解析】
【分析】
(1)利用极坐标与直角坐标互化公式进行求解;(2)先设,进而表达出的中点P的坐标,用点到直线距离和三角函数的有界性求出最小值及点P的极坐标.
(1)
由,所以点M的直角坐标为,
化简得:,即,
(2)
设,则,
所以的中点P到直线l的距离
,
当,即,时,,
此时,所以,
由,,可知P点的极坐标为
所以的中点P到直线l的距离的最小值为,此时点P极坐标为.
23.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)利用代入法后转化为二次函数后配方即可求解;
(2)利用的等效转换后利用基本不等式即可求证.
(1)
解:由题意得:
当时,的最小值为
(2)
当且仅当,即时取等号;
四川省大数据精准教学联盟2023届高三第二次统一监测理数试题: 这是一份四川省大数据精准教学联盟2023届高三第二次统一监测理数试题,文件包含大数据理科数学试题pdf、四川大数学二统答案pdf等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
四川省大数据精准教学联盟2023届高三第二次统一监测理数试题: 这是一份四川省大数据精准教学联盟2023届高三第二次统一监测理数试题,文件包含大数据理科数学试题pdf、四川大数学二统答案pdf等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
四川省大数据精准教学联盟2023届高三第二次统一监测理数试题: 这是一份四川省大数据精准教学联盟2023届高三第二次统一监测理数试题,文件包含四川大数学二统答案pdf、大数据理科数学试题pdf等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。